Next: 3.7 INSIEMI LIMITE Up: 3. TEORIA QUALITATIVA Previous: 3.5 GRADIENTI Indice Indice analitico
Sommario Un punto di equilibrio il cui linearizzato ha esponenti di
Lyapounov sia positivi che negativi è instabile; infatti ci sono
necessariamente delle curve per cui l'equilibrio è il limite per
![]() , e anche altre per cui è limite per
, e anche altre per cui è limite per
![]() . Tali curve sono uniche. Se non ci sono autovalori con
parte reale nulla un intorno di un punto di equilibrio può essere
descritto come il prodotto cartesiano di un pozzo per una
sorgente.
. Tali curve sono uniche. Se non ci sono autovalori con
parte reale nulla un intorno di un punto di equilibrio può essere
descritto come il prodotto cartesiano di un pozzo per una
sorgente.
Consideriamo un sistema dinamico continuo in ![]() , e facciamo
l'ipotesi che abbia un punto di equilibrio nell'origine; sviluppando
il campo vettoriale nell'origine si ottiene:
, e facciamo
l'ipotesi che abbia un punto di equilibrio nell'origine; sviluppando
il campo vettoriale nell'origine si ottiene:
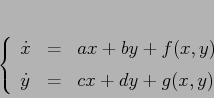
![\begin{displaymath}
\frac{d{ }}{d{t}}\,\left[\begin{array}{c}{x}\\
{y}\end{arr...
...A=\left[\begin{array}{cc}{a}&{b}\\
{c}&{d}\end{array}\right]
\end{displaymath}](img979.png)
Abbiamo già visto le proprietà qualitative del sistema
dinamico nonlineare nel caso di un pozzo o di una
sorgente, che si verificano per ![]() ; infatti in tal
caso, se
; infatti in tal
caso, se ![]() gli esponenti di Lyapounov sono tutti
negativi, mentre se
gli esponenti di Lyapounov sono tutti
negativi, mentre se ![]() sono tutti positivi.
sono tutti positivi.
Definizione:
Questo si verifica per ![]() : gli autovalori di
: gli autovalori di
![]() sono reali e con prodotto negativo.
sono reali e con prodotto negativo.
Un'altra affermazione equivalente è che il sistema linearizzato ha un punto di equilibrio di tipo sella.
Se ![]() gli autovalori sono distinti, supponiamo che siano
gli autovalori sono distinti, supponiamo che siano
![]() con
con
![]() ; quindi esistono due autovettori
linearmente indipendenti, e usando questi come nuova base si
può portare il sistema dinamico nella forma più semplice
; quindi esistono due autovettori
linearmente indipendenti, e usando questi come nuova base si
può portare il sistema dinamico nella forma più semplice
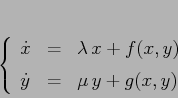
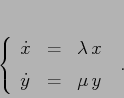
Esempio:
Una curva eccezionale è una curva la cui immagine ![]() contiene
delle soluzioni del sistema dinamico che hanno o limite diverso, o
anche lo stesso limite ma vi arrivano con tangente differente (o verso
differente, come in Figura 2.5), rispetto ad altre
soluzioni ``arbitrariamente vicine'' (cioè con condizioni iniziali
in un sistema fondamentale di intorni di
contiene
delle soluzioni del sistema dinamico che hanno o limite diverso, o
anche lo stesso limite ma vi arrivano con tangente differente (o verso
differente, come in Figura 2.5), rispetto ad altre
soluzioni ``arbitrariamente vicine'' (cioè con condizioni iniziali
in un sistema fondamentale di intorni di ![]() ). Questa definizione si
può intendere sia per
). Questa definizione si
può intendere sia per ![]() che per
che per ![]() .
.
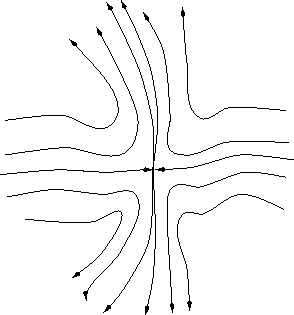 |
Una sella nonlineare ha sempre delle soluzioni che tendono al
punto di equilibrio sia per ![]() che per
che per
![]() ; le immagini di queste soluzioni formano due
insiemi
; le immagini di queste soluzioni formano due
insiemi ![]() , localmente chiusi nell'intorno del punto di
equilibrio, ed aventi per frontiera delle curve eccezionali.
, localmente chiusi nell'intorno del punto di
equilibrio, ed aventi per frontiera delle curve eccezionali.
Dimostrazione:
Dopo aver trasformato il sistema dinamico nella forma:
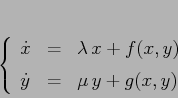
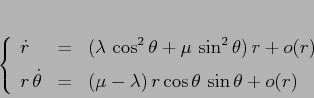
 |
Allora in tutti i punti di ![]() vale
vale ![]() .
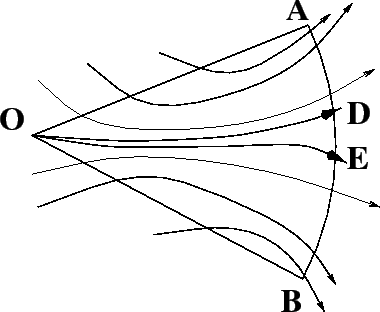
Consideriamo il bordo di
.
Consideriamo il bordo di ![]() ,
che è costituito dai due segmenti
,
che è costituito dai due segmenti ![]() ed
ed
![]() e dall'arco di circonferenza
e dall'arco di circonferenza ![]() , dove
, dove ![]() è
l'origine,
è
l'origine, ![]() ha coordinate polari
ha coordinate polari
![]() e
e ![]() ha
coordinate polari
ha
coordinate polari
![]() . Sul segmento
. Sul segmento ![]() vale
vale ![]() , e sul segmento
, e sul segmento ![]() vale
vale ![]() , cioè le soluzioni entrano in
, cioè le soluzioni entrano in ![]() (non
considerando il punto
(non
considerando il punto ![]() che è di equilibrio). Invece
sull'arco
che è di equilibrio). Invece
sull'arco ![]() vale
vale ![]() , quindi le soluzioni escono da
, quindi le soluzioni escono da
![]() .
.
Consideriamo una soluzione
![]() che entra in
che entra in ![]() da uno dei due segmenti
da uno dei due segmenti ![]() ,
, ![]() (escluso
(escluso ![]() ). Lungo tale
soluzione
). Lungo tale
soluzione ![]() è crescente, e non può avere un limite
finito e
è crescente, e non può avere un limite
finito e ![]() (altrimenti sui valori limite si avrebbe
(altrimenti sui valori limite si avrebbe
![]() , e questo non accade in
, e questo non accade in ![]() ). Perciò tale
soluzione esce da
). Perciò tale
soluzione esce da ![]() lungo
lungo ![]() . Chiamiamo
. Chiamiamo ![]() la parte di
la parte di
![]() da cui escono le soluzioni che entrano da
da cui escono le soluzioni che entrano da ![]() , e
, e ![]() quella parte di
quella parte di ![]() da cui escono le soluzioni entrate in
da cui escono le soluzioni entrate in
![]() . I due insiemi sono separati (le soluzioni non possono
incrociarsi, per non violare l'unicità delle soluzioni per
una condizione iniziale data) ed aperti. Poiché l'arco
. I due insiemi sono separati (le soluzioni non possono
incrociarsi, per non violare l'unicità delle soluzioni per
una condizione iniziale data) ed aperti. Poiché l'arco ![]() è un insieme continuo (è parametrizzato dal segmento
è un insieme continuo (è parametrizzato dal segmento
![]() ), deve esistere almeno un
elemento separatore
), deve esistere almeno un
elemento separatore ![]() che non appartiene né a
che non appartiene né a ![]() né a
né a
![]() . Prendiamo la soluzione
. Prendiamo la soluzione
![]() per
per ![]() : per
: per
![]() non può uscire da
non può uscire da ![]() , ma per lo stesso
ragionamento fatto sopra
, ma per lo stesso
ragionamento fatto sopra ![]() non può tendere ad un limite
non può tendere ad un limite
![]() , quindi la soluzione per
, quindi la soluzione per ![]() ha come punto limite per
ha come punto limite per
![]() la sella nonlineare
la sella nonlineare ![]() .
.
Se ne deduce che ![]() non è vuoto; esso contiene tutte le soluzioni
che appartengono al tratto di
non è vuoto; esso contiene tutte le soluzioni
che appartengono al tratto di ![]() compreso tra
compreso tra ![]() e
e ![]() , che
può essere o un singolo punto
, che
può essere o un singolo punto ![]() o un arco
o un arco ![]() compresi i due
estremi
compresi i due
estremi ![]() ed
ed ![]() . Nel primo caso c'è una sola curva eccezionale
per
. Nel primo caso c'è una sola curva eccezionale
per ![]() , che è l'unica in
, che è l'unica in ![]() ad avere
ad avere ![]() come punto limite per
come punto limite per
![]() ; nel secondo caso, arbitrariamente vicino alle due curve
per
; nel secondo caso, arbitrariamente vicino alle due curve
per ![]() ed
ed ![]() esistono soluzioni che, per
esistono soluzioni che, per ![]() , non tendono
a
, non tendono
a ![]() .
.
La dimostrazione relativa a ![]() è sostanzialmente la
stessa, salvo che occorre considerare un settore
è sostanzialmente la
stessa, salvo che occorre considerare un settore
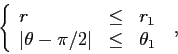
In realtà le proprietà degli autovalori reali
![]() che servono nella dimostrazione relativa a
che servono nella dimostrazione relativa a ![]() sono:
sono:
![]() e
e ![]() ; non serve che
; non serve che ![]() . Ne segue
che l'esistenza di curve eccezionali e dell'insieme
. Ne segue
che l'esistenza di curve eccezionali e dell'insieme ![]() vale anche nel caso di un punto di equilibrio degenere
con un esponente di Lyapounov nullo ed uno positivo.
Simmetricamente, l'esistenza di curve eccezionali e
dell'insieme
vale anche nel caso di un punto di equilibrio degenere
con un esponente di Lyapounov nullo ed uno positivo.
Simmetricamente, l'esistenza di curve eccezionali e
dell'insieme ![]() vale nel caso di un punto di equilibrio
degenere con un esponente di Lyapounov nullo ed uno negativo.
vale nel caso di un punto di equilibrio
degenere con un esponente di Lyapounov nullo ed uno negativo.
Nel caso di due autovalori positivi ma distinti
![]() si ha una sorgente, ed il sistema
linearizzato è del tipo nodo. Usando ancora la
stessa definizione, visto che
si ha una sorgente, ed il sistema
linearizzato è del tipo nodo. Usando ancora la
stessa definizione, visto che ![]() e che
e che
![]() in un settore opportunamente scelto, si mostra
l'esistenza di curve eccezionali che sono diverse dalle altre
non per il limite per
in un settore opportunamente scelto, si mostra
l'esistenza di curve eccezionali che sono diverse dalle altre
non per il limite per ![]() , che in questo caso è la
sorgente per tutte le soluzioni vicine, ma per la tangente con
cui si avvicinano al limite; si veda la Figura 2.1.
, che in questo caso è la
sorgente per tutte le soluzioni vicine, ma per la tangente con
cui si avvicinano al limite; si veda la Figura 2.1.
Definizione:
Una curva differenziabile in ![]() , si dice separatrice
di un sistema dinamico continuo, se la sua immagine
, si dice separatrice
di un sistema dinamico continuo, se la sua immagine ![]() ha le
seguenti due proprietà:
ha le
seguenti due proprietà:
Si potrebbe dimostrare che una terza condizione (c) segue da (a) e (b):
Esempio:
Esempio:
Mentre nel caso lineare si può accertare l'esistenza di separatrici approfittando dell'espressione esplicita di tutte le soluzioni, nel caso nonlineare l'esistenza di curve separatrici non è in generale ovvia. Perciò è importante poter decidere dell'esistenza di separatrici sulla base delle sole proprietà del linearizzato, per esempio sulla base dei soli esponenti di Lyapounov.
Una sella nonlineare ha sempre
esattamente due separatrici, che sono l'insieme delle condizioni
iniziali che hanno quel punto di equilibrio come limite per
![]() e per
e per ![]() , e si chiamano perciò,
rispettivamente, separatrice stabile e
separatrice instabile.
La separatrice stabile è tangente, nel punto di
equilibrio, all'autospazio dell'autovalore negativo del linearizzato;
quella instabile è tangente all'autospazio dell'autovalore positivo.
, e si chiamano perciò,
rispettivamente, separatrice stabile e
separatrice instabile.
La separatrice stabile è tangente, nel punto di
equilibrio, all'autospazio dell'autovalore negativo del linearizzato;
quella instabile è tangente all'autospazio dell'autovalore positivo.
Usando la Figura 3.9, questo teorema afferma che i
due punti ![]() ed
ed ![]() coincidono, e la soluzione per
coincidono, e la soluzione per ![]() fa parte
della separatrice, che contiene anche il punto di equilibrio
fa parte
della separatrice, che contiene anche il punto di equilibrio ![]() e
la curva eccezionale dall'altra parte.
e
la curva eccezionale dall'altra parte.
Dimostrazione (facoltativa):
Supponiamo che la sella nonlineare sia nell'origine, e che sia della forma
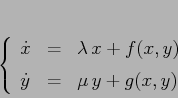
Questo deriva dal fatto che
l'equazione alle variazioni
per l'orbita con condizioni iniziali nell'origine
coincide con il sistema linearizzato nell'origine, il cui
flusso integrale è
![]() .
.
L'origine è un punto fisso iperbolico per il
sistema dinamico discreto ![]() , con un valore fisso
, con un valore fisso ![]() : gli
autovalori del linearizzato nel punto fisso sono
: gli
autovalori del linearizzato nel punto fisso sono
![]() e
e
![]() . Applicando a
. Applicando a ![]() il teorema delle
separatrici stabile e instabile troviamo una separatrice
instabile tangente all'asse
il teorema delle
separatrici stabile e instabile troviamo una separatrice
instabile tangente all'asse ![]() nell'origine, ed una stabile tangente
all'asse
nell'origine, ed una stabile tangente
all'asse ![]() .
.
Per concludere la dimostrazione del teorema occorre mostrare che le
separatrici di ![]() sono invarianti per
sono invarianti per
![]() per ogni
per ogni ![]() , non solo per il
, non solo per il ![]() usato nella
dimostrazione. Questo deriva dal fatto che tali curve invarianti
esistono per ogni
usato nella
dimostrazione. Questo deriva dal fatto che tali curve invarianti
esistono per ogni ![]() , per il teorema di
esistenza delle curve eccezionali, e perciò devono
coincidere per non violare
l'unicità delle separatrici di
, per il teorema di
esistenza delle curve eccezionali, e perciò devono
coincidere per non violare
l'unicità delle separatrici di ![]() .
.
Per una dimostrazione più approfondita si veda [Hartmann 64].
Un teorema analogo afferma l'unicità delle curve eccezionali dei nodi.
Le due soluzioni appartenenti alla separatrice, che hanno il punto di
sella come limite per ![]() , si allontanano dall'equilibrio
al crescere di
, si allontanano dall'equilibrio
al crescere di ![]() ; se consideriamo tali soluzioni sull'intervallo
massimo di definizione (nel senso del teorema di
continuazione delle soluzioni), ciascuna di esse ha per
immagine una curva in
; se consideriamo tali soluzioni sull'intervallo
massimo di definizione (nel senso del teorema di
continuazione delle soluzioni), ciascuna di esse ha per
immagine una curva in ![]() . Tuttavia non è detto che l'immagine di
questa curva sia chiusa in
. Tuttavia non è detto che l'immagine di
questa curva sia chiusa in ![]() . È proprio il
riavvolgersi delle separatrici e il loro intersecarsi in modo
complicato uno dei fenomeni alla base del caos, come
sarà discusso nel Capitolo 6. Anche nei casi più
semplici, le separatrici si ``avvolgono'' tra loro, e con questo
determinano le proprietà qualitative di un sistema dinamico nel
piano, come nei due esempi seguenti.
. È proprio il
riavvolgersi delle separatrici e il loro intersecarsi in modo
complicato uno dei fenomeni alla base del caos, come
sarà discusso nel Capitolo 6. Anche nei casi più
semplici, le separatrici si ``avvolgono'' tra loro, e con questo
determinano le proprietà qualitative di un sistema dinamico nel
piano, come nei due esempi seguenti.
Esempio:
 |
Esempio:
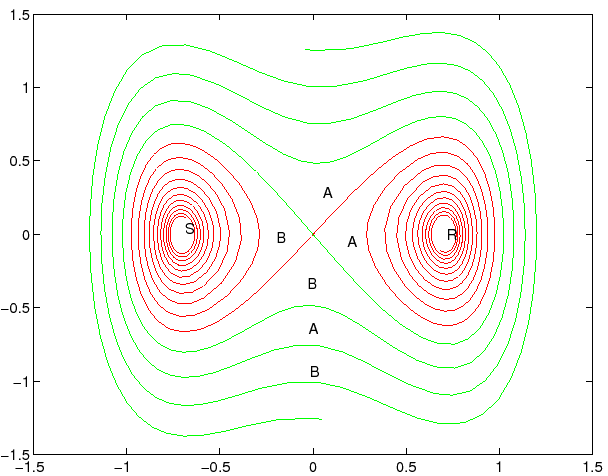 |
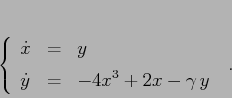
L'origine è un punto di sella nonlineare; tracciate le separatrici,
è facile rendersi conto che i bacini di attrazione dei due punti
asintoticamente stabili (corrispondenti ai minimi del potenziale in
![]() ed
ed ![]() ) si avvolgono l'uno attorno
all'altro a spirale, come illustrato in Figura 3.11.
) si avvolgono l'uno attorno
all'altro a spirale, come illustrato in Figura 3.11.
Esercizio
Dato il sistema newtoniano dissipativo:
In ![]() ci sono solo tre tipi di punti di equilibrio iperbolici: i
pozzi, le selle e le sorgenti, a seconda che il numero di esponenti di
Lyapounov negativi sia 2, 1 o 0. Dal teorema di esistenza della
separatrice instabile segue che un punto di equilibrio iperbolico o
è un pozzo o è instabile.
ci sono solo tre tipi di punti di equilibrio iperbolici: i
pozzi, le selle e le sorgenti, a seconda che il numero di esponenti di
Lyapounov negativi sia 2, 1 o 0. Dal teorema di esistenza della
separatrice instabile segue che un punto di equilibrio iperbolico o
è un pozzo o è instabile.
In effetti questo segue già dal più semplice teorema di
esistenza delle curve eccezionali. Inoltre lo stesso
risultato vale anche per un punto di equlibrio iperbolico in ![]() con
con ![]() .
.
In un intorno abbastanza piccolo del punto di equilibrio, il comportamento qualitativo delle orbite del sistema dinamico può essere deciso in base alla sua parte lineare. Per i pozzi e le sorgenti questo deriva dai teoremi della Sezione 3.2. Nel caso della sella nonlineare, il comportamento qualitativo può essere descritto da quello della sella lineare, ma in questo caso la natura ``qualitativa'' (o meglio, topologica) del risultato si manifesta con una perdita di differenziabilità nella corrispondenza tra i due sistemi, come nel teorema seguente.
Ogni sella nonlineare ha un intorno ![]() tale che esiste un
omeomorfismo
tale che esiste un
omeomorfismo ![]() tra
tra ![]() ed un intorno
ed un intorno ![]() di una sella
lineare, tale che le soluzioni dei due sistemi dinamici sono
coniugate tra loro: se
di una sella
lineare, tale che le soluzioni dei due sistemi dinamici sono
coniugate tra loro: se ![]() è il flusso
integrale del sistema nonlineare, e
è il flusso
integrale del sistema nonlineare, e ![]() quello del sistema
lineare, allora
quello del sistema
lineare, allora
Andrea Milani 2009-06-01