Next: B. ESEMPI DI COMPITI Up: A. REQUISITI DI ALGEBRA, Previous: A.4 SERIE DI FUNZIONI Indice Indice analitico
Definizione:
Definizione:
Queste definizioni valgono sia per gli spazi a dimensione
finita, come ![]() , sia per gli spazi di funzioni che hanno
dimensione infinita, nel senso che sono spazi vettoriali ma non
hanno un numero finito di generatori.
, sia per gli spazi di funzioni che hanno
dimensione infinita, nel senso che sono spazi vettoriali ma non
hanno un numero finito di generatori.
Esempio:
Se l'applicazione ![]() è una contrazione di uno spazio metrico
completo
è una contrazione di uno spazio metrico
completo ![]() , allora
, allora ![]() ha un unico punto unito, cioè esiste uno ed
un solo
ha un unico punto unito, cioè esiste uno ed
un solo ![]() tale che
tale che ![]() .
.
Il punto unito (cioè fisso) è costruito per
approssimazioni successive,
come limite della successione
![]() che,
comunque sia scelto il punto iniziale
che,
comunque sia scelto il punto iniziale ![]() , converge nello spazio
metrico completo
, converge nello spazio
metrico completo ![]() in quanto successione di Cauchy.
in quanto successione di Cauchy.
Definizione:
Una contrazione è una funzione lipschitziana di uno
spazio in se stesso, con costante di Lipschitz ![]() .
.
Una funzione lipschitziana è anche continua, anzi
uniformemente continua, in quanto per ogni ![]() esiste
un
esiste
un
![]() tale che
tale che
![]() per ogni
coppia
per ogni
coppia ![]() con
con
![]() . Se
. Se
![]() , la
lipschizianità nel punto
, la
lipschizianità nel punto ![]() equivale alla limitatezza del rapporto
incrementale nel punto
equivale alla limitatezza del rapporto
incrementale nel punto ![]() in direzione
in direzione ![]() ; si può mostrare che
implica la differenziabilità in quasi tutti i punti di
; si può mostrare che
implica la differenziabilità in quasi tutti i punti di ![]() (cioè
a meno di insiemi di misura nulla). Viceversa, ogni funzione
(cioè
a meno di insiemi di misura nulla). Viceversa, ogni funzione ![]() differenziabile di classe
differenziabile di classe ![]() su di un aperto
su di un aperto
![]() è localmente lipschitziana, nel senso che la diseguaglianza
di Lipschitz è soddisfatta in ogni aperto limitato
è localmente lipschitziana, nel senso che la diseguaglianza
di Lipschitz è soddisfatta in ogni aperto limitato ![]() con
chiusura contenuta in
con
chiusura contenuta in ![]() : la costante di Lipschitz non supera
la somma dei massimi moduli di tutte le derivate parziali di
: la costante di Lipschitz non supera
la somma dei massimi moduli di tutte le derivate parziali di ![]() sulla chiusura di
sulla chiusura di ![]() .
.
Siano
![]() un aperto,
un aperto,
![]() un
intervallo e
un
intervallo e
![]() un campo vettoriale
uniformemente lipschitziano nella prima variabile, ovvero tale
che, per una costante
un campo vettoriale
uniformemente lipschitziano nella prima variabile, ovvero tale
che, per una costante ![]() ,
,
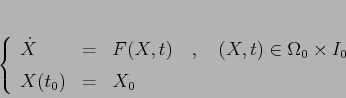
La dimostrazione del teorema precedente è costruttiva:
un'applicazione pratica è il ragionamento che conduce alla
definizione di esponenziale di matrice. Il teorema delle
contrazioni, infatti, mostra l'esistenza di un punto fisso
dell'operatore
![]() , sullo spazio metrico completo
, sullo spazio metrico completo ![]() delle funzioni continue, definito da
delle funzioni continue, definito da
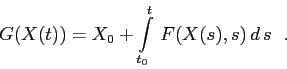
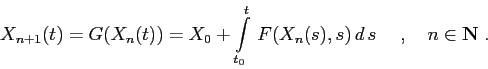
Sia
![]() una funzione reale non negativa, definita su un aperto
una funzione reale non negativa, definita su un aperto
![]() . Se la
. Se la ![]() è dominata dal suo integrale,
nel senso che per due costanti
è dominata dal suo integrale,
nel senso che per due costanti ![]() ,
, ![]() ,
,
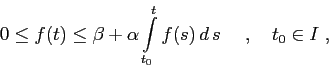
Il teorema che segue applica la diseguaglianza di Gronwall per fornire
dettagli precisi sulla dipendenza dai dati iniziali del flusso
![]() di un sistema dinamico.
di un sistema dinamico.
Siano
![]() un aperto,
un aperto,
![]() un intervallo e
un intervallo e
![]() un
campo vettoriale uniformemente lipschitziano nella prima
variabile, con costante di Lipschitz
un
campo vettoriale uniformemente lipschitziano nella prima
variabile, con costante di Lipschitz ![]() . Se
. Se ![]() e
e ![]() sono
soluzioni dell'equazione
sono
soluzioni dell'equazione
La dipendenza delle soluzioni dalle condizioni iniziali è non solo continua, ma ha una costante di Lipschitz che può essere calcolata a partire dalla costante di Lipschitz del secondo membro, e che cresce esponenzialmente al crescere dell'intervallo di tempo. Si confronti con il teorema di convergenza del metodo di Eulero e con la definizione di esponente di Lyapounov.
Siano
![]() un aperto,
un aperto,
![]() e
e
![]() un campo vettoriale (anche dipendente
dal tempo) di classe
un campo vettoriale (anche dipendente
dal tempo) di classe
![]() . Allora esiste un intorno di
. Allora esiste un intorno di
![]() in
in
![]() su cui il flusso integrale
su cui il flusso integrale
![]() dell'equazione differenziale
dell'equazione differenziale
La matrice jacobiana ![]() del flusso
del flusso
Siano
![]() un aperto,
un aperto, ![]() un intervallo,
un intervallo,
![]() un campo vettoriale
uniformemente lipschitziano nella prima variabile e
un campo vettoriale
uniformemente lipschitziano nella prima variabile e ![]() una
condizione iniziale in
una
condizione iniziale in ![]() . Per il
problema alle condizioni iniziali
. Per il
problema alle condizioni iniziali
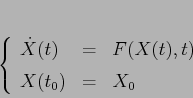
Se il sistema dinamico è autonomo, cioè
![]() ,
per ogni condizione iniziale
,
per ogni condizione iniziale ![]() l'ampiezza dell'intervallo
massimale
l'ampiezza dell'intervallo
massimale ![]() della soluzione
della soluzione
![]() non dipende
dall'istante iniziale.
non dipende
dall'istante iniziale.
Consideriamo il flusso integrale di un sistema dinamico
Per ![]()
![]() , cioè
, cioè ![]() (identità).
Laddove il flusso è definito, vale la proprietà di composizione
(identità).
Laddove il flusso è definito, vale la proprietà di composizione
Nel caso di un'equazione differenziale
non autonoma
si può comunque definire un flusso integrale
Bibliografia :
Andrea Milani 2009-06-01