Next: 6.4 REGIONI ORDINATE Up: 6. CAOS Previous: 6.2 ORBITE PERIODICHE Indice Indice analitico
Sommario In presenza di punti omoclinici si può costruire
un modello esplicito del comportamento caotico, definito mediante
operazioni semplici come lo scorrimento di una sequenza biinfinita di
cifre. I punti che corrispondono a questo modello formano un insieme
omeomorfo al prodotto di due insiemi di Cantor, che sta nella chiusura
dell'insieme delle orbite periodiche.
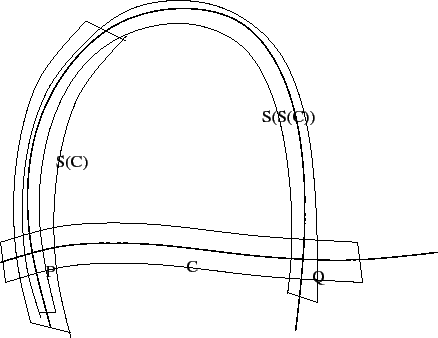
Per descrivere in modo esplicito l'intreccio omoclinico che
risulta dall'intersezione della separatrice stabile con quella
instabile consideriamo un intorno di un segmento su una delle
due. Sia ![]() un punto fisso iperbolico,
un punto fisso iperbolico, ![]() un
punto omoclinico trasversale, e sia
un
punto omoclinico trasversale, e sia ![]() un intorno del segmento
un intorno del segmento
![]() sulla separatrice stabile
sulla separatrice stabile ![]() (Figura 6.11). L'immagine
(Figura 6.11). L'immagine ![]() è accorciata lungo la
separatrice stabile e allungata lungo quella instabile; queste
deformazioni sono sempre più accentuate in
è accorciata lungo la
separatrice stabile e allungata lungo quella instabile; queste
deformazioni sono sempre più accentuate in
![]() e
così via, finché per un certo intero
e
così via, finché per un certo intero ![]() l'immagine
l'immagine ![]() è
ripiegata come un ferro di cavallo che tocca
è
ripiegata come un ferro di cavallo che tocca ![]() dai due lati, cioè
dai due lati, cioè
![]() ha due componenti connesse.
ha due componenti connesse.
 |
Possiamo supporre che un opportuno cambiamento differenziabile di
coordinate trasformi il segmento ![]() della curva separatrice stabile
in un segmento di retta e
della curva separatrice stabile
in un segmento di retta e ![]() in un quadrato per semplificare la
figura e la discussione seguente. Sempre a meno di opportuni
cambiamenti di coordinate differenziabili, si può allora descrivere
la mappa
in un quadrato per semplificare la
figura e la discussione seguente. Sempre a meno di opportuni
cambiamenti di coordinate differenziabili, si può allora descrivere
la mappa ![]() ristretta a
ristretta a ![]() mediante una sequenza di tre
trasformazioni:
mediante una sequenza di tre
trasformazioni: ![]() con
con ![]() ; prima
; prima ![]() viene compresso
lungo l'asse corrispondente alla separatrice stabile (supponiamo che
sia l'asse
viene compresso
lungo l'asse corrispondente alla separatrice stabile (supponiamo che
sia l'asse ![]() ), poi viene dilatato lungo l'asse corrispondente alla
separatrice instabile (supponiamo che sia l'asse
), poi viene dilatato lungo l'asse corrispondente alla
separatrice instabile (supponiamo che sia l'asse ![]() ), infine viene
ripiegato a ferro di cavallo
(Figura 6.12). L'intersezione
), infine viene
ripiegato a ferro di cavallo
(Figura 6.12). L'intersezione
![]() consiste di due rettangoli
consiste di due rettangoli ![]() e
e ![]() con
con ![]() sottointervalli di
sottointervalli di ![]() . Possiamo supporre che la matrice jacobiana di
. Possiamo supporre che la matrice jacobiana di
![]() su
su ![]() sia
sia
![\begin{displaymath}
DS^n=\left[\begin{array}{cc}{\lambda}&{0}\\
{0}&{\lambda^{-1}}\end{array}\right]
\end{displaymath}](img2255.png)
![\begin{displaymath}
DS^n=\left[\begin{array}{cc}{-\lambda}&{0}\\
{0}&{-\lambda^{-1}}\end{array}\right]
\end{displaymath}](img2258.png)
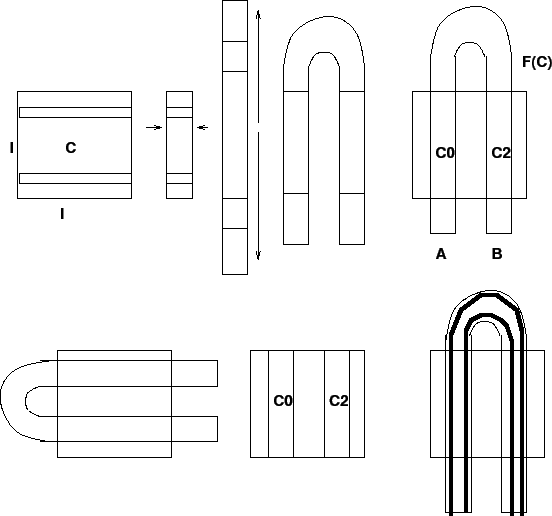 |
A questo punto iteriamo la mappa ![]() , e consideriamo le immagini
successive:
, e consideriamo le immagini
successive:
![]() sono quattro rettangoli
verticali (Figura 6.12),
sono quattro rettangoli
verticali (Figura 6.12),
![]() otto rettangoli, e in generale
otto rettangoli, e in generale
![]() sono
sono ![]() rettangoli verticali, prodotto di
rettangoli verticali, prodotto di ![]() sottointervalli di
sottointervalli di ![]() disgiunti per
disgiunti per ![]() . Allora
. Allora
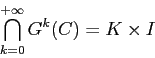
Un ragionamento del tutto analogo vale per la mappa inversa ![]() :
:
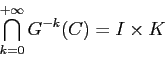
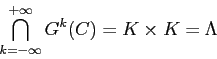
La discussione precedente costituisce una traccia di dimostrazione del seguente enunciato: se un punto fisso iperbolico ha un punto omoclinico trasversale, allora esiste un insieme (chiuso, compatto, senza parte interna) invariante per un'iterata della mappa, che è omeomorfo al prodotto di due insiemi di Cantor. Per una presentazione più dettagliata si rimanda al lavoro originale [Smale 67].
La dinamica definita dalla mappa ![]() ristretta all'insieme di Smale
ristretta all'insieme di Smale
![]() ha delle proprietà molto interessanti, ed è suscettibile
di una descrizione esplicita che va sotto il nome di
dinamica simbolica.
Per ottenere questa descrizione introduciamo il concetto
di storia di un punto
ha delle proprietà molto interessanti, ed è suscettibile
di una descrizione esplicita che va sotto il nome di
dinamica simbolica.
Per ottenere questa descrizione introduciamo il concetto
di storia di un punto ![]() . Se
. Se ![]() sta in
sta in ![]() deve appartenere o a
deve appartenere o a ![]() o a
o a ![]() ; allora il suo `presente' è
descritto qualitativamente dal simbolo 0 oppure dal simbolo 2.
; allora il suo `presente' è
descritto qualitativamente dal simbolo 0 oppure dal simbolo 2. ![]() a sua volta appartiene o a
a sua volta appartiene o a ![]() o a
o a ![]() , quindi l'immediato
`futuro' è descritto qualitativamente da un'altra scelta tra gli
stessi due simboli; lo stesso vale per l'immediato passato, che sarà
descritto da 0 se
, quindi l'immediato
`futuro' è descritto qualitativamente da un'altra scelta tra gli
stessi due simboli; lo stesso vale per l'immediato passato, che sarà
descritto da 0 se
![]() , da 2 se
, da 2 se
![]() . In
generale definiamo la sequenza biinfnita (funzione a valori interi)
. In
generale definiamo la sequenza biinfnita (funzione a valori interi)
![]() in questo modo:
in questo modo:
Le storie possibili dei punti di ![]() , cioè le funzioni
definite su
, cioè le funzioni
definite su ![]() e a valori in
e a valori in ![]() , formano l'insieme
, formano l'insieme
![]() a cui si può attribuire una topologia nel modo seguente: un
intorno della sequenza
a cui si può attribuire una topologia nel modo seguente: un
intorno della sequenza ![]() è costituito da tutte le sequenze
è costituito da tutte le sequenze
![]() tali che
tali che
Lemma:
Dimostrazione del lemma:
La continuità di questa applicazione si può verificare
direttamente dalla definizione della topologia su
![]() ,
tenendo conto che la mappa
,
tenendo conto che la mappa ![]() è pure continua.
è pure continua.
Il passaggio più delicato consiste nel verificare che la
corrispondenza è
biunivoca. Se due punti hanno la stessa storia per il futuro
(![]() per
per ![]() ) la differenza tra loro nella coordinata
) la differenza tra loro nella coordinata
![]() è minore di
è minore di ![]() per ogni
per ogni ![]() , cioè le coordinate
, cioè le coordinate ![]() sono
uguali. Se hanno la stessa storia passata (
sono
uguali. Se hanno la stessa storia passata (![]() per
per ![]() )
la differenza nella
)
la differenza nella ![]() è minore di
è minore di ![]() per ogni
per ogni
![]() , cioè le coordinate
, cioè le coordinate ![]() sono uguali.
Se la corrispondenza tra punti e la loro storia è continua e
biunivoca, allora è un omeomorfismo.
sono uguali.
Se la corrispondenza tra punti e la loro storia è continua e
biunivoca, allora è un omeomorfismo.
Il lemma implica una proprietà veramente notevole della
dinamica sull'insieme di Smale: ogni storia è possibile. Non importa
quanto `strana' sia una storia, cioè una sequenza di simboli ![]() ,
esisterà sempre un punto
,
esisterà sempre un punto ![]() la cui orbita si comporta
proprio così. Per esempio, non importa quanto sia lunga una
sequenza di
la cui orbita si comporta
proprio così. Per esempio, non importa quanto sia lunga una
sequenza di ![]() , cioè per quante iterazioni
un'orbita resti in
, cioè per quante iterazioni
un'orbita resti in ![]() (più vicino al punto omoclinico
(più vicino al punto omoclinico ![]() che al punto fisso
che al punto fisso ![]() ), a questi può sempre seguire sia un 2 che
uno 0. Questo vuol dire che il comportamento di ogni orbita è
imprevedibile. Non importa quanto bene si conoscono le condizioni
iniziali, se queste sono note con un'approssimazione finita esiste
sempre un orizzonte di prevedibilità, cioè un numero di iterazioni
dopo le quali condizioni iniziali indistinguibili (secondo
l'accuratezza disponibile) danno luogo a orbite lontane tra loro.
), a questi può sempre seguire sia un 2 che
uno 0. Questo vuol dire che il comportamento di ogni orbita è
imprevedibile. Non importa quanto bene si conoscono le condizioni
iniziali, se queste sono note con un'approssimazione finita esiste
sempre un orizzonte di prevedibilità, cioè un numero di iterazioni
dopo le quali condizioni iniziali indistinguibili (secondo
l'accuratezza disponibile) danno luogo a orbite lontane tra loro.
Il lemma fornisce un'altra costruzione dell'equivalenza topologica
dell'insieme di Smale con un prodotto di due insiemi di
Cantor. Infatti si può considerare il caso particolare di insieme di
Cantor ottenuto come segue: partendo dal segmento ![]() se ne
tolga il terzo centrale
se ne
tolga il terzo centrale ![]() . Quindi si tolga il terzo
centrale da ciascuno dei due intervalli rimasti, cioè si tolga
. Quindi si tolga il terzo
centrale da ciascuno dei due intervalli rimasti, cioè si tolga
![]() . Si prosegua togliendo al passo
. Si prosegua togliendo al passo ![]() -esimo
da ciascuno dei
-esimo
da ciascuno dei ![]() intervalli chiusi rimasti il suo terzo centrale
aperto. L'intersezione infinita di tutti gli insiemi ottenuti dopo
ogni passo è un insieme di Cantor
intervalli chiusi rimasti il suo terzo centrale
aperto. L'intersezione infinita di tutti gli insiemi ottenuti dopo
ogni passo è un insieme di Cantor ![]() ; gli
insiemi di Cantor
sono tutti omeomorfi. Però quello ottenuto con la particolare
procedura del terzo centrale può essere descritto come segue:
consideriamo i punti di
; gli
insiemi di Cantor
sono tutti omeomorfi. Però quello ottenuto con la particolare
procedura del terzo centrale può essere descritto come segue:
consideriamo i punti di ![]() rappresentati con uno sviluppo in
base tre, cioè con ``cifre''
rappresentati con uno sviluppo in
base tre, cioè con ``cifre'' ![]() . Allora
. Allora ![]() è l'insieme
di tutti i numeri tra 0 e 1 tali che nel loro sviluppo ternario non
appare la cifra 1. (Attenzione:
è l'insieme
di tutti i numeri tra 0 e 1 tali che nel loro sviluppo ternario non
appare la cifra 1. (Attenzione: ![]() può essere descritto come
può essere descritto come
![]() , e così
, e così
![]() .)
.)
Di conseguenza l'omeomorfismo tra ![]() e
e ![]() si può
ottenere considerando la ``storia presente e futura''
si può
ottenere considerando la ``storia presente e futura''
![]() come un punto di
come un punto di ![]() e la ``storia passata''
e la ``storia passata''
![]() come un
altra coordinata pure
come un
altra coordinata pure ![]() .
.
Definizione:
Si può verificare che lo scorrimento di Bernoulli è un omeomorfismo.
Se una sequenza ![]() è interpretata come la storia di un punto
è interpretata come la storia di un punto
![]() , allora la sua immagine mediante lo scorrimento di
Bernoulli è la storia di un altro punto, che ha la stessa storia
una sola iterazione prima. È facile verificare che questa è la
storia dell'immagine
, allora la sua immagine mediante lo scorrimento di
Bernoulli è la storia di un altro punto, che ha la stessa storia
una sola iterazione prima. È facile verificare che questa è la
storia dell'immagine ![]() dello stesso punto. In altre parole se
dello stesso punto. In altre parole se
![]() è l'omeomorfismo tra i punti dell'insieme di Smale e le loro
storie,
è l'omeomorfismo tra i punti dell'insieme di Smale e le loro
storie,
![]() , ovvero
, ovvero
![]() .
.
Proprietà:
Dimostrazione:
I punti periodici contenuti nell'insieme di Smale sono tutti iperbolici.
Diamo un enunciato formale del teorema di Smale, che lega i punti
omoclinici alle proprietà dell'insieme ![]() .
.
Definizione:
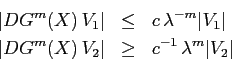
Esempio:
Esempio:
Sia ![]() un diffeomorfismo di
un diffeomorfismo di ![]() (oppure
(oppure ![]() ),
), ![]() un suo punto
fisso iperbolico,
un suo punto
fisso iperbolico, ![]() un punto omoclinico trasversale. Allora
esiste un intero
un punto omoclinico trasversale. Allora
esiste un intero ![]() ed un insieme compatto
ed un insieme compatto ![]() , contenente sia
, contenente sia
![]() che
che ![]() , invariante ed iperbolico per
, invariante ed iperbolico per ![]() , tale che la
restrizione di
, tale che la
restrizione di ![]() a
a ![]() è coniugata mediante omeomorfismi
allo scorrimento di Bernoulli
è coniugata mediante omeomorfismi
allo scorrimento di Bernoulli ![]() sulle sequenze biinfinite di
due simboli, ossia
sulle sequenze biinfinite di
due simboli, ossia
Andrea Milani 2009-06-01