6.2 ORBITE PERIODICHE

Sommario Anche i punti che formano orbite periodiche, se iperbolici, hanno delle separatrici. Per trovare le orbite periodiche si possono usare procedimenti di approssimazione, come il metodo di Newton. Una volta individuata l'orbita periodica, la costruzione delle separatrici è la stessa. Le intersezioni delle separatrici formano punti omoclinici ed eteroclinici, con intrecci ancora più complessi di quelli omoclinici dei punti fissi.

Ricerca di orbite periodiche

Abbiamo visto che il punto $X_3=(0,\pi)$ è periodico di periodo due, e nella Figura 6.1 si notano due ``isole'' di curve invarianti che circondano l'orbita costitutita dai punti $X_3$ e $X_4=(\pi, \pi)$. Si nota anche una regione caotica che circonda le due isole, che sembra una versione ``a due buchi'' della regione caotica che circonda il punto fisso iperbolico $(\pi,0)$. È quindi logico chiedersi se esista anche un punto periodico iperbolico di periodo due, cioè un punto $X_5$ tale che $S(X_5)=X_6$ e $S(X_6)=S^2(X_5)=X_5$ con matrice jacobiana

$$A^{(2)}= A(X_6)\, A(X_5)$$

che ha moltiplicatori di Lyapounov maggiori e minori di uno. Dalla Figura si può immaginare che il punto $X_5$ dovrebbe essere vicino al punto $X^0=(1.9, 3.5)$. Ma come trovare un'orbita periodica?

Un procedimento molto efficace è il metodo di Newton, che generalizza a due dimensioni il metodo che si usa per trovare le soluzioni di un'equazione nonlineare in una variabile. Noi stiamo cercando un punto $X^*$ tale che $S^2(X^*)=X^*$. Proviamo a calcolare l'immagine (per $S^2$) del punto che abbiamo scelto come prima approssimazione: naturalmente $S^2(X^0)\neq X^0$, ma da questa prima approssimazione si può ricavare una correzione da applicare per avvicinarsi ad $X^*$: sviluppando in serie di Taylor in $X^0$

$$X^*=S^2(X^*)=S^2(X^0)+ A^{(2)}(X^0)\, (X^*-X^0)+ {\cal O} \left(\vert X^*-X^0\vert^2\right)$$

da cui se trascuriamo gli infinitesimi di ordine superiore al primo (rispetto a $\vert X^*-X^0\vert$)

$$X^*\simeq S^2(X^0)+ A^{(2)}(X^0)\, (X^*-X^0)\ .$$

Questa equazione non è esatta, tuttavia il punto che soddisfa a

$$X^1= S^2(X^0)+ A^{(2)}(X^0)\, (X^1-X^0)\ .$$

sarà un'approssimazione di $X^*$ migliore di $X^0$. Risolvendo per $X^1-X^0$

$$X^1-X^0= S^2(X^0)-X^0 + A^{(2)}(X^0)\, (X^1-X^0)$$

$$\left[I - A^{(2)}(X^0)\right]\;\left(X^1-X^0\right)= S^2(X^0)-X^0$$

e se la matrice $I-A^{(2)}$ è invertibile, cioè se $A^{(2)}$ non ha autovalore 1 (si noti che questo è vero sia per un punto periodico iperbolico che per uno ellittico, e per continuità delle derivate resterà vero in un intorno di questi) si ricava

$$X^1=X^0+ \left[I - A^{(2)}(X^0)\right]^{-1}\;\left(S^2(X^0)-X^0\right) \ .$$

Tuttavia $S^2(X^1)\neq X^1$, e a questo punto si itera, cioè si calcola

$$X^{k+1}=X^k+ \left[I - A^{(2)}(X^k)\right]^{-1}\;\left(S^2(X^k)-X^k\right) \ .$$

fino a convergenza della successione $X^k$. Poiché il metodo di Newton, se converge, converge molto rapidamente, si ottiene una ottima approssimazione del punto fisso con un piccolo numero di iterazioni.

Un programma Matlab per cercare punti periodici (di periodo 2, o anche di periodo maggiore con una piccola modifica) della mappa standard, usando il metodo di Newton: stmapnew.m

Nel nostro caso troviamo (dopo soltanto 4 iterazioni) un punto periodico di periodo due in $X_5\simeq (1.8134710074,3.6269420149)$. Si tratta di un punto periodico iperbolico: gli autovalori di $A^{(2)}(X_5)$ sono $\lambda_1\simeq 0.38\;,\; \lambda_2\simeq 2.64$.

Separatrici dei punti periodici iperbolici

A questo punto si applica il teorema delle separatrici stabile e instabile al punto fisso iperbolico della mappa $S^2$. Partendo di nuovo da un'approssimazione lineare con un segmento, si ottiene iterando la mappa $S^2$ una buona approssimazione di un lungo segmento sulla separatrice instabile; operando nello stesso modo con l'autospazio stabile e la mappa $S^{-2}$ si traccia la separatrice stabile.

Figura 6.8: Segmenti iniziali della separatrice instabile (a destra del punto iperbolico $X_5$) e separatrice stabile. Le due separatrici si ricongiungono e formano, se prolungate ancora, dei punti omoclinici vicino al punto $X_6=S(X_5)$.

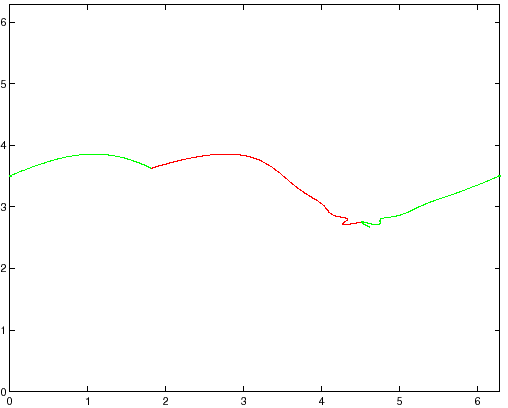La situazione è un poco più complicata rispetto al caso del punto fisso iperbolico, perché di separatrici ne esistono quattro, due uscenti dal punto iperbolico $X_5$ e due uscenti dal punto iperbolico $X_6=S(X_5)$. Così il segmento di separatrice stabile uscente da $X_5$ tracciato nella Figura 6.8 ha già formato delle intersezioni con la separatrice instabile uscente da $X_6$, e quella instabile uscente da $X_5$ ha già intersecato, nel segmento mostrato nella figura, la separatrice stabile uscente da $X_6$.

Definizione:

Se $P, Q$ sono due punti periodici iperbolici di periodo $r$ del sistema dinamico discreto $S$, un punto che appartiene all'intersezione della separatrice stabile di uno dei due con la separatrice instabile dell'altro si dice punto omoclinico se $P$ e $Q$ appartengono alla stessa orbita periodica, punto eteroclinico tra $P$ e $Q$ se le orbite di $P$ e $Q$ sono distinte.

Se $W_s(P)$ e $W_s(Q)$ sono le immagini delle due separatrici stabili, $W_i(P)$ e $W_i(Q)$ quelle delle due separatrici instabili, l'insieme dei punti omoclinici (o eteroclinici) è


$$\left[W_s(P)\cap W_i(Q)\right] \cup \left[W_i(P)\cap W_s(Q)\right] \ .$$



Sia i punti omoclinici che quelli eteroclinici sono doppiamente asintotici. Però i punti omoclinici hanno l'orbita di $P$ e $Q$ sia come $\alpha$-limite che come $\omega$-limite. I punti eteroclinici hanno come $\alpha$-limite l'orbita di $P$ e come $\omega$-limite l'orbita di $Q$, oppure viceversa.

La definizione si generalizza al caso in cui i due punti $P$ e $Q$ hanno periodi diversi $p$ e $q$, rispettivamente; in questo caso basta considerare il minimo comune multiplo $r$ di $p$ e $q$, che è un periodo comune per i due punti.

Figura 6.9: L'intreccio omoclinico delle separatrici del punto iperbolico di periodo 2.

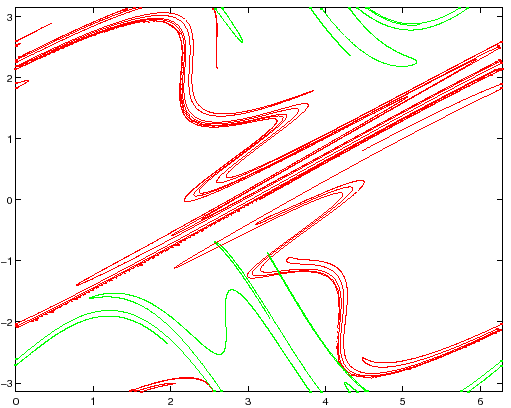
Vale la proprietà analoga a quella dei punti omoclinici di un punto fisso: se un punto è omoclinico o eteroclinico, lo stesso vale per tutta la sua orbita. Ne segue che i punti omoclinici ed eteroclinici devono formare intrecci del genere descritto da Poincaré. Nella Figura 6.9 si può osservare uno di questi intrecci, contenente punti omoclinici all'orbita di periodo 2 formata da $X_5$ ed $X_6$. È chiaro che questo intreccio omoclinico ha un ruolo importante nel generare la regione caotica che circonda le ``isole'' stabili vicino ai punti ellittici di periodo 2 (vedi Figura 6.1).

Un programma Matlab per tracciare le separatrici del punto iperbolico (trovato con stmanew) della mappa standard di periodo 2 (o anche di periodo maggiore, con una piccola modifica) : stmasep2.m

Sempre guardando la Figura 6.1, ma con occhi addestrati dall'esperienza fatta con i punti di periodo 2, si possono notare due catene di isole che devono avere al centro punti di periodo 3 ellittici (una si trova al di sopra, l'altra al di sotto dei punti periodici di periodo due). Le isole sono circondate da regioni caotiche generate dall'intersezione delle separatrici di punti di periodo tre iperbolici. Si può usare il metodo di Newton, applicato alla mappa $S^3$, per trovare i punti iperbolici di periodo tre, quindi tracciare le separatrici e mostrare l'esistenza di punti omoclinici.

Nella Figura 4.6 si possono trovare addirittura delle catene di isole che suggeriscono la presenza di punti di periodo 4 e 5, sia ellittici che iperbolici. La presenza di orbite periodiche di periodo arbitrariamente alto conferisce alle orbite della mappa standard, come quelle delle Figure 4.5, 4.6 e 6.1, il caratteristico aspetto ``frattale'', con particolari configurazioni di punti che si ripetono in scala sempre più piccola.

Figura 6.10: Un tratto della separatrice instabile del punto fisso iperbolico, e un tratto della separatrice stabile del punto iperbolico di periodo 2, per $h=1.3$. Dei punti eteroclinici sono visibili, per esempio nei pressi del punto $(x,y)=(3,-1)$.

Resta da capire se esistono connessioni eterocliniche tra tutte le orbite periodiche iperboliche di cui abbiamo parlato, oppure se, per $h=1$, il toro è suddiviso in fasce (che fanno un giro della variabile $x$, non della $y$) separate e invarianti per la mappa $S$. La risposta è che per $h=1$ la mappa standard non ha più nessuna curva invariante di Moser che sia di circolazione, cioè che faccia un giro completo per la variabile $x$. Ne segue che condizioni iniziali vicine al punto fisso iperbolico $X_2=(\pi,0)$ hanno orbite che possono passare vicino ai punti di periodo 2 iperbolici $X_5$ e $X_6$, e quindi andare a passare vicino a $(\pi, 2\pi)$ che naturalmente è ancora $X_2$. Esiste in effetti una catena di connessioni eterocliniche che consente di attraversare il toro facendo un giro completo per la variabile $y$. Questo però è un risultato tutt'altro che elementare che non è possibile spiegare in un corso di questo livello; si veda [Greene 79].

I collegamenti formati da punti eteroclinici, specie tra orbite con periodi diversi, possono formare intrecci ancora più complicati di quelli generati dai punti omoclinici. Possiamo per esempio immaginare, nella mappa standard del pendolo, un collegamento eteroclinico tra il punto fisso iperbolico e l'orbita di periodo due iperbolica. Per valori del passo $h$ un po' maggiori di 1 questo collegamento esiste, come si può vedere nella Figura 6.10.