2.3 AUTOVALORI REALI

Sommario Il calcolo dell'esponenziale di matrice può essere eseguito in un diverso sistema di riferimento. Se il nuovo riferimento è costruito mediante gli autovettori della matrice data, il calcolo è più semplice; per una matrice diagonalizzabile (in campo reale) ci si riduce a calcolare l'esponenziale di una matrice diagonale.

Cambiamenti di coordinate

Supponiamo di sottoporre il sistema dinamico lineare $\dot X =AX$ ad un cambiamento di coordinate lineare:

$$Y=B\,X\hspace{5mm},\hspace{5mm}con\ B \ \mbox{matrice di tipo}\ n\times n.$$

Si suppone che la matrice $B$ sia invertibile, $det\, B\neq 0$. Allora l'equazione differenziale si trasforma in questo modo:

$$\dot Y = B\, \dot X = B\, A\, X = B\, A\, B^{-1}\, Y = C\, Y$$

cioè è ancora un sistema dinamico lineare, la cui matrice $C=BAB^{-1}$ è ottenuta per coniugio da $A$. Perciò la soluzione del sistema trasformato in funzione della condizione iniziale $Y(0)=Y_0$ sarà espressa mediante l'esponenziale di matrice:

$$Y(t)=\exp(Ct)\, Y_0\hspace{5mm},\hspace{5mm}Y_0=B\, X_0\ \ ;$$

la relazione tra le soluzioni delle due equazioni per $X$ e per $Y$ è data da:

$$X(t)=B^{-1}\, Y(t)=B^{-1}\exp(Ct)\, Y_0=B^{-1}\exp(Ct)\,B\,X_0\ \ .$$

Per convincersi che la soluzione è la stessa, basta considerare che

$$\left(BAB^{-1}\right)^i=B\,A^i\,B^{-1}$$

e quindi

$$\exp(Ct)=\exp\left(BAB^{-1}t\right)=\sum_{i=0}^\infty \frac{\... ...!}= \sum_{i=0}^\infty B\frac{A^it^i}{i!}B^{-1}=B\exp(At)B^{-1}$$

dove l'ultimo passaggio è lecito perché la moltiplicazione di matrici è un'operazione continua e la serie esponenziale è convergente.

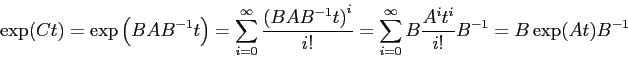
Si noti che le matrici che esprimono i flussi integrali sono pure coniugate, ed il coniugio è eseguito con la stessa matrice $B$ del cambiamento di coordinate.

Si può quindi sempre studiare il sistema dinamico lineare $\dot X =AX$ in un qualunque sistema di riferimento; la matrice $A$ si trasforma come la matrice di una trasformazione dello spazio ambiente ${\bf R}^n$ in sé, cioè per coniugio con la matrice che esprime il cambiamento di coordinate. Perciò ha senso cercare un sistema di coordinate in cui la trasformazione definita da $A$ abbia una forma semplice, risolvere il sistema dinamico lineare in quel sistema di coordinate, e poi ritornare al sistema originale usando la trasformazione inversa.

Esercizio Trovare il cambiamento di coordinate lineare che cambia

$$A= \left[\begin{array}{cc}{0}&{1}\\ {1}&{0}\end{array}\ri... ...\left[\begin{array}{cc}{1}&{0}\\ {0}&{-1}\end{array}\right]$$

(Soluzione)

Diagonalizzazione

Poiché le proprietà geometriche (a meno di trasformazioni lineari di coordinate) dei sistemi dinamici lineari dipendono solo dalla classe di equivalenza della matrice $A$ a meno di coniugio, è logico cercare di utilizzare le quantità che sono invarianti per coniugio, come gli autovalori; si utilizzeranno quindi le nozioni di base della sezione A.1.

Definizione:

Una matrice quadrata $A$ $n\times n$ si dice diagonalizzabile se esiste una base $\{ V_1, V_2,\ldots,V_n\}$ di autovettori con autovalori reali $\lambda_1, \lambda_2,\ldots,\lambda_n$.

In questo caso la matrice $A$ è equivalente per coniugio ad una matrice diagonale:

$$B\, A \,B^{-1}=D=diag\,[\lambda_1, \lambda_2, \ldots, \lambda_n]\;,$$

con sulla diagonale principale gli autovalori $\lambda_i,\; i=1,n$. Infatti:

$$A\, V_i=\lambda_i V_i\hspace{5mm},\hspace{5mm}i=1,\ldots, n$$

per definizione di autovalore $\lambda_i$ ed autovettore $V_i$; mettendo insieme le equazioni precedenti in forma matriciale, se $V$ è la matrice quadrata con colonne $V_i$, che è invertibile perchè i $V_i$ sono linearmente indipendenti:

$$AV=VD\Longleftrightarrow V^{-1}\,A\,V=D$$

quindi l'applicazione, che nella base canonica è espressa dalla matrice $A$, nella base $\{V_i\}$ è espressa dalla matrice diagonale $D$. La matrice $B$ che esprime il cambiamento di coordinate $Y=BX$ è $B=V^{-1}$.

Se gli autovalori sono tutti reali e distinti allora la matrice è diagonalizzabile: gli autovettori di autovalori diversi sono linearmente indipendenti, e quindi costituiscono una base.

Se la matrice $A$ è diagonalizzabile, allora tutte le orbite del sistema dinamico lineare $\dot X =AX$ si possono esprimere mediante combinazioni lineari di funzioni esponenziali $\exp(\lambda_it)$, dove i coefficienti del tempo negli esponenti sono gli autovalori $\lambda_i$ della matrice $A$. Dimostrazione:

Se $AV=VD$, con $V$ una matrice invertibile di autovettori, allora nelle coordinate $Y=V^{-1}\, X$ (quelle ottenute usando gli autovettori $\{V_i\}$ come base) il sistema dinamico consiste di equazioni differenziali scalari disaccoppiate:

$$\dot {y_i}=\lambda_i \, y_i\hspace{5mm},\hspace{5mm}i=1,\ldots,n$$


le cui soluzioni sono $y_i(t)=e^{\lambda_i\,t}\,y_i(0)$, cioè

$$Y(t)=diag\left[e^{\lambda_1\,t},e^{\lambda_2\, t},\ldots,e^{\lambda_n\, t}\right]\, Y_0$$


da cui si trova la soluzione nelle coordinate originali $(x_j)$:

$$X(t)=V\, diag\left[e^{\lambda_1\,t},e^{\lambda_2\, t},\ldots,e^{\lambda_n\, t}\right]\, V^{-1}\, X_0$$


per cui ciascuna coordinata $x_j(t)$ è combinazione lineare di funzioni esponenziali

 C.D.D.

Dimensione 2

In dimensione $n=2$ dato il sistema dinamico:

$$\left\{\begin{array}{lcl} {\displaystyle \dot x} & {\displa... ...y}{cc}{a_{11}}&{a_{12}}\\ {a_{21}}&{a_{22}}\end{array}\right]$$

per trovare gli autovalori si usa l'equazione caratteristica:

$$det\, \left[ A-\lambda\,I\right] =0$$

ottenuta eguagliando a zero il polinomio caratteristico, in questo caso un polinomio di grado 2, i cui coefficienti sono espressi in termini del determinante di $A$ e della traccia di $A$ ( $tr\, A=a_{11}+a_{22}$):

$$det\, \left[ A-\lambda\,I\right] =\lambda^2 -tr\,A\,\lambda +det\, A=0$$

Il numero di soluzioni reali e distinte dell'equazione caratteristica dipende in questo caso solo dal segno del discriminante dell'equazione di secondo grado:

$$\Delta= (tr\, A)^2 -4\, det\,A = (a_{11}-a_{22})^2 +4\,a_{12}a_{21}$$

Per $\Delta>0$ ci sono due autovalori reali distinti $\lambda_1,\lambda_2$, e quindi due autovettori reali e linearmente indipendenti $V_1$ e $V_2$. Per $\Delta<0$ gli autovalori sono complessi, non esistono autovettori reali, quindi l'applicazione definita dalla matrice $A$ non potrà essere in forma diagonale in nessun sistema di riferimento reale.

Esercizio

$$\dot X =A\, X \hspace{5mm},\hspace{5mm}A=\left[\begin{array}{cc}{1}&{2}\\ {1}&{3}\end{array}\right]$$

Scrivere esplicitamente il flusso integrale come combinazione di esponenziali. (Soluzione)

Nel caso $\Delta=0$ non si può decidere se la matrice è diagonalizzabile soltanto dal valore di $\Delta$; nei due casi seguenti:

$$A=\left[\begin{array}{cc}{\lambda_1}&{0}\\ {0}&{\lambda_1}\... ...array}{cc}{\lambda_1}&{1}\\ {0}&{\lambda_1}\end{array}\right]$$

la matrice $A$ è già diagonale, mentre la matrice $Z$ non è diagonalizzabile, poiché tutti gli autovettori sono linearmente dipendenti da $(1,0)$.

Nel caso $n>2$ decidere se una matrice è diagonalizzabile, e diagonalizzarla esplicitamente, può essere tutt'altro che semplice. Per il teorema fondamentale dell'algebra ogni matrice $n\times n$ ha $n$ autovalori, reali o complessi, contati con la loro molteplicità algebrica. Però se $n\geq 5$ non esiste alcun algoritmo esplicito per risolvere l'equazione caratteristica. Le matrici simmetriche sono sempre diagonalizzabili (vedi Sezione A.1).

Nodi e selle

Consideriamo il caso di dimensione $n=2$ ed una matrice $A$ con autovalori reali distinti: esistono due autovettori $V_1, V_2$ tali che:

$$A\,V_1=a\, V_1 \hspace{5mm},\hspace{5mm} A\,V_2=b\, V_2$$

e quindi nella base $\{V_1,V_2\}$ la matrice si trasforma per coniugio con $B^{-1}=V=[V_1,V_2]$:

$$B\,A\,B^{-1}= \left[\begin{array}{cc}{a}&{0}\\ {0}&{b}\end{array}\right]$$

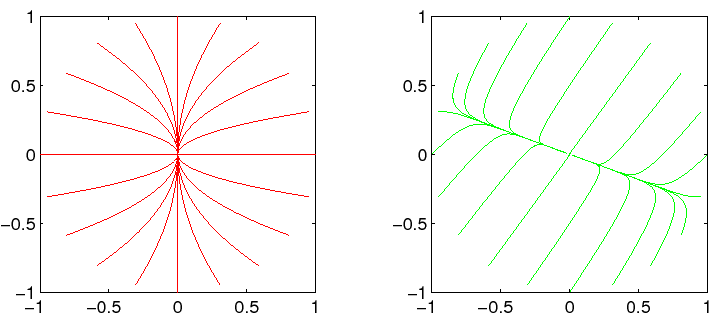
Il comportamento qualitativo delle orbite si può studiare nel sistema in forma canonica, a cui ci si può ricondurre a meno di trasformazioni lineari:

$$\left\{\begin{array}{lcl} {\displaystyle \dot x} & {\displ... ...y} & {\displaystyle=} &{\displaystyle b y} \end{array}\right.$$

Il flusso integrale è dato, in funzione delle due condizioni iniziali $x_0$ e $y_0$, dalle due funzioni esponenziali, visto che le equazioni sono disaccoppiate:

$$\left\{\begin{array}{lcl} {\displaystyle x(t)} & {\display... ...laystyle=} &{\displaystyle e^{b\,t}\, y_0} \end{array}\right.$$

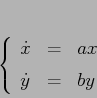
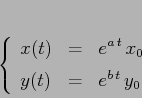
La traiettoria, cioè la curva descritta in ${\bf R}^2$ dalle soluzioni (senza la legge oraria, cioè senza la parametrizzazione in funzione di $t$), si può ricavare (limitandosi al primo quadrante, le traiettorie relative agli altri tre quadranti si ottengono per simmetria) elevando la soluzione per $x(t)$ alla potenza $b$, e quella per $y(t)$ alla potenza $a$, e facendo il quoziente (per $y_0\neq 0$):

$$\frac{x^b}{y^a}=\frac{x_0^b}{y_0^a}=cost .$$

Figura 2.1: Due esempi di punti di equilibrio del tipo nodo; quello a sinistra aveva un'equazione in forma canonica.

Figura 2.2: Due esempi di punti di equilibrio del tipo sella; quello a sinistra aveva un'equazione in forma canonica.

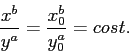
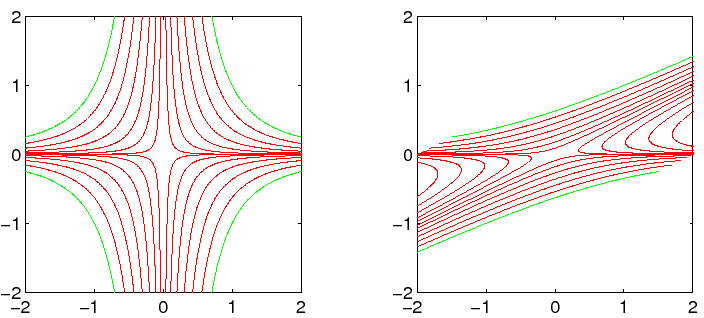Il comportamento qualitativo dipende solo dal segno di $a$ e $b$:

• $a<0, b<0$ Tutte le orbite (tranne quella ferma nel punto di equilibrio nell'origine) vanno all'infinito per $t\to -\infty$, e hanno come limite per $t\to +\infty$ l'origine. Le traiettorie per $x_0\neq 0$ sono:
  
  $$y=y_0\;\left(\frac x{x_0} \right)^{b/a}$$
  
  
  e quindi:

  *

  $b<a<0$ Tutte le orbite con $x_0\neq 0$ tendono all'origine con tangente che tende all'orizzontale, salvo la curva eccezionale $x=0$. Il punto di equilibrio nell'origine si dice del tipo nodo.

  *

  $a<b<0$ Tutte le orbite con $x_0\neq 0$ tendono all'origine con tangente che tende alla verticale, salvo la curva eccezionale $y=0$; anche questo si dice di tipo nodo.

  *

  $a=b<0$ Tutte le orbite tendono all'origine con tangenti differenti, in tutte le direzioni.

• $b<0<a$ Tutte le orbite con $x_0\neq 0, y_0\neq 0$ vanno all'infinito per $t\to \pm \infty$. Ci sono però due curve eccezionali: $y=0$, sulla quale per le orbite tendono all'origine per $t\to -\infty$, ed $x=0$, sulla quale le orbite tendono all'origine per $t\to +\infty$. Le traiettorie (per $x_0\neq 0$) sono:
  
  $$y=y_0\;\left(\frac {x_0}x \right)^{-b/a}$$
  
  
  e quindi per $x_0\neq 0, y_0\neq 0$ le traiettorie sono asintotiche all'asse $x$ per $t\to +\infty$, asintotiche all'asse $y$ per $t\to -\infty$. Il punto di equilibrio nell'origine si dice del tipo sella.

• $a=0, b<0$ Le traiettorie sono rette $x=cost$, e le orbite per $t\to +\infty$ tendono alla retta $y=0$ di punti di equilibrio.

• Tutti gli altri casi si ottengono dai precedenti cambiando il segno a $t$, quindi il comportamento per $t\to +\infty$ si scambia con quello per $t\to -\infty$.

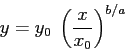
Esercizio Determinare le orbite del sistema dinamico

$$\dot X=AX\;,\; A=\left[\begin{array}{cc}{-1}&{4}\\ {-1}&{-6}\end{array}\right]$$

e descrivere l'equazione (implicita) delle traiettorie nel piano $(x_1,x_2)$. (Soluzione)