ESERCIZIO 2.1
- Da
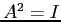 segue
segue
- Poiché la matrice è diagonale:,
- Calcolando le potenze successive di
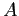 si ottiene
si ottiene
da cui
ESERCIZIO 2.2 Dal punto di vista algebrico, si possono facilmente calcolare coefficienti 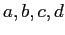 tali che
tali che
ossia
con soluzione  ,
, 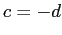 ,
, 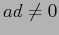 ; la matrice del cambiamento di base è del tipo
; la matrice del cambiamento di base è del tipo
![$\left[\begin{array}{cc}{a}&{a}\\
{-d}&{d}\end{array}\right]$](img2648.png) con
con 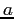 e
e 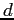 non nulli.
non nulli.
In questo caso, il passaggio di coordinate cercato può essere dedotto anche geometricamente. L'applicazione lineare rappresentata dalla matrice 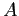 scambia i vettori
scambia i vettori 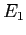 e
e 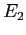 della vecchia base: è una simmetria rispetto alla loro bisettrice, i cui vettori
della vecchia base: è una simmetria rispetto alla loro bisettrice, i cui vettori
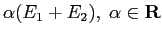 sono lasciati fissi. Rispetto ad una nuova base con primo vettore
sono lasciati fissi. Rispetto ad una nuova base con primo vettore 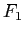 sull'asse di simmetria e secondo vettore
sull'asse di simmetria e secondo vettore 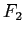 ad esso ortogonale, l'applicazione si rappresenta con la matrice
ad esso ortogonale, l'applicazione si rappresenta con la matrice 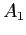 , e la matrice
, e la matrice 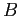 del cambiamento di base è l'inversa di quella avente per colonne
del cambiamento di base è l'inversa di quella avente per colonne 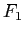 ed
ed 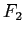 :
:
ovvero
come ottenuto algebricamente.
ESERCIZIO 2.3 Gli autovalori ed autovettori di 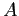 sono:
sono:
con
ESERCIZIO 2.4 Autovalori e autovettori
e con ![$V=[V_1, V_2]$](img2662.png)
per cui
PROBLEMA 2.5 Se in ogni punto 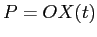 il vettor tangente alla curva
il vettor tangente alla curva 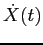 è proporzionale ad un vettore ottenuto ruotando
è proporzionale ad un vettore ottenuto ruotando 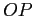 dell'angolo orientato
dell'angolo orientato 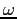 , la curva
, la curva 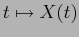 è soluzione del sistema dinamico
è soluzione del sistema dinamico
Gli autovalori di 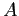 (
(
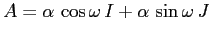 ) sono complessi:
) sono complessi:
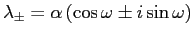 , ed
, ed 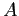 è già in forma canonica. Quindi per ogni punto
è già in forma canonica. Quindi per ogni punto 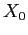 del piano passa una curva
del piano passa una curva
Le traiettorie sono, in genere, spirali intorno al fuoco 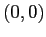 : l'unico caso in cui sono limitate è quello in cui
: l'unico caso in cui sono limitate è quello in cui
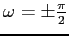 , allorché
, allorché
descrive delle circonferenze centrate nell'origine.
Per
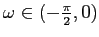 le spirali si allargano in senso antiorario, per
le spirali si allargano in senso antiorario, per
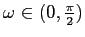 in senso orario (secondo il segno di
in senso orario (secondo il segno di 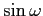 ); per
); per
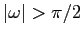 le spirali si stringono verso l'origine, infine per
le spirali si stringono verso l'origine, infine per 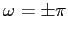 risulta
risulta
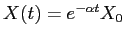 , con traiettorie rettilinee uscenti dall'origine.
, con traiettorie rettilinee uscenti dall'origine.
ESERCIZIO 2.6
ESERCIZIO 2.7 Sommario dei calcoli:
Le condizioni iniziali con 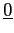 come limite per
come limite per 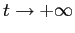 sono quelle parallele a
sono quelle parallele a 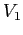 , quelle con limite
, quelle con limite 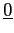 per
per 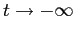 sono combinazioni lineari di
sono combinazioni lineari di 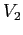 e
e 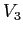 , dove
, dove 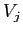 sono le colonne della matrice
sono le colonne della matrice 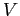 .
.
ESERCIZIO 2.8 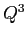 ha diversi da zero solo quelli di posto
ha diversi da zero solo quelli di posto 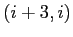 , se esistono; e così via. Quindi nell'esponenziale il coefficiente di posto
, se esistono; e così via. Quindi nell'esponenziale il coefficiente di posto 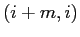 sarà
sarà 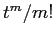 ; sulla diagonale
; sulla diagonale 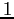 e sopra la diagonale principale
e sopra la diagonale principale 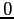 .
.
ESERCIZIO 2.9 Risulta
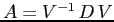 , con
, con
Nelle coordinate 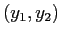 , relative alla base della forma canonica, le orbite sono
, relative alla base della forma canonica, le orbite sono
ESERCIZIO 2.10 Resta da vedere quali valori possono assumere 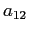 e
e 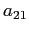 , dato che
, dato che
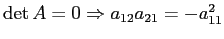 . Se
. Se 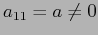 , anche
, anche 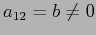 ,
,
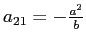 e
e
se 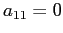 , le ulteriori possibilità sono
, le ulteriori possibilità sono
ESERCIZIO 2.11 Se è vero che 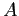 ha un solo autovalore
ha un solo autovalore 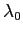 , la matrice
, la matrice
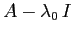 ha solo l'autovalore
ha solo l'autovalore 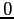 e quindi ha traccia nulla:
e quindi ha traccia nulla:
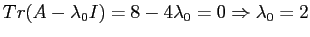 .
.
La forma canonica 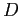 di
di 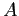 ha
ha 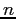 blocchi di Jordan, dove
blocchi di Jordan, dove 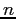 è la dimensione del
è la dimensione del 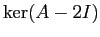 . Dallo studio della caratteristica di
. Dallo studio della caratteristica di
risulta  (la seconda riga è multipla della terza, la prima è somma della terza e della quarta, linearmente indipendenti).
(la seconda riga è multipla della terza, la prima è somma della terza e della quarta, linearmente indipendenti).
Poiché 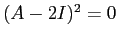 , entrambi i blocchi hanno ordine
, entrambi i blocchi hanno ordine 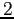 : in tal caso è facile determinare esplicitamente una base per i blocchi nilpotenti. Se infatti
: in tal caso è facile determinare esplicitamente una base per i blocchi nilpotenti. Se infatti
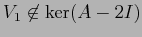 ,
,
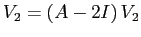 è indipendente da
è indipendente da 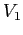 e
e
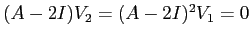 , e se (analogamente) si sceglie un
, e se (analogamente) si sceglie un
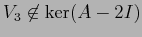 indipendente da
indipendente da 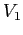 anche
anche 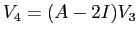 è tale che
è tale che 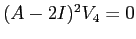 ; per esempio, se
; per esempio, se
la forma canonica 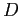 di
di 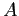 rispetto a
rispetto a
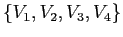 e la matrice
e la matrice 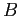 del cambiamento di base sono
del cambiamento di base sono
Calcolando 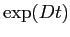 si ottiene il flusso integrale:
si ottiene il flusso integrale:
Le traiettorie tendono all'infinito per 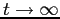 , e all'origine per
, e all'origine per 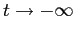 , per qualunque punto iniziale
, per qualunque punto iniziale 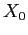 .
Andrea Milani
2009-06-01
.
Andrea Milani
2009-06-01
![\begin{eqnarray*}X(t)&=&\sum\limits_{n=0}^\infty \left [\frac{A^{2n}t^{2n}}{(2n)...
...c}{0}&{\sinh(t)}\\
{\sinh(t)}&{0}\end{array}\right]\right )X_0 \end{eqnarray*}](img2639.png)
![\begin{displaymath}X(t)=\left[\begin{array}{cc}{e^t}&{0}\\
{0}&{e^{-t}}\end{array}\right]X_0 \end{displaymath}](img2640.png)
![\begin{displaymath}A^2=\left[\begin{array}{ccc}
{0}&{0}&{0}\\ {0}&{0}&{0}\\ {1}&{0}&{0}\end{array}\right] \;,\;A^3={\underline{\underline 0}}\;,\end{displaymath}](img2641.png)
![\begin{eqnarray*}X(t)&=&\exp(At)X_0=\left (I+At+\frac12A^2t^2\right )X_0\\ &=&\l...
...\\ {x^0_2+x^0_1t}\\ {x_3^0+x_2^0t+x_1^0 t^2/2}\end{array}\right] \end{eqnarray*}](img2642.png)
![]() tali che
tali che
![\begin{displaymath}\left[\begin{array}{cc}{a}&{b}\\
{c}&{d}\end{array}\right]\...
...begin{array}{cc}{a}&{b}\\
{c}&{d}\end{array}\right]\neq 0\;, \end{displaymath}](img2643.png)
![\begin{displaymath}\left[\begin{array}{cc}{b}&{a}\\
{d}&{c}\end{array}\right]=\left[\begin{array}{cc}{a}&{b}\\
{-c}&{-d}\end{array}\right] \end{displaymath}](img2644.png)
![$\left[\begin{array}{cc}{a}&{a}\\
{-d}&{d}\end{array}\right]$](img2648.png) con
con ![\begin{displaymath}B^{-1}=\left[\begin{array}{cc}{\alpha}&{-\beta}\\
{\alpha}&{\beta}\end{array}\right]\;,\end{displaymath}](img2655.png)
![\begin{displaymath}B=\frac1{2\alpha\beta}\left[\begin{array}{cc}{\beta}&{\beta}\\
{-\alpha}&{\alpha}\end{array}\right]\;,\end{displaymath}](img2656.png)
![]() sono:
sono:
![\begin{displaymath}\lambda_1=2+\sqrt{3} \hspace{5mm},\hspace{5mm}V_1=\left[\begin{array}{c}{1}\\
{(1+\sqrt{3})/2}\end{array}\right]\end{displaymath}](img2657.png)
![\begin{displaymath}\lambda_2=2-\sqrt{3} \hspace{5mm},\hspace{5mm}V_2=\left[\begin{array}{c}{-1-\sqrt{3}}\\
{1}\end{array}\right]\end{displaymath}](img2658.png)
![\begin{displaymath}X(t)=\left[\begin{array}{cc}{1}&{-1-\sqrt{3}}\\
{(1+\sqrt{3...
...ight]\; \left[\begin{array}{c}{u_0}\\
{v_0}\end{array}\right]\end{displaymath}](img2659.png)
![\begin{displaymath}\left[\begin{array}{c}{x_0}\\
{y_0}\end{array}\right]=\left...
...ight]\; \left[\begin{array}{c}{u_0}\\
{v_0}\end{array}\right]\end{displaymath}](img2660.png)
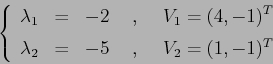
![\begin{displaymath}V^{-1}\; A \; V= \left[\begin{array}{cc}{-2}&{\phantom{-}0}\\
{\phantom{-}0}&{-5}\end{array}\right] \end{displaymath}](img2663.png)
![\begin{displaymath}\exp(At)= V\; \left[\begin{array}{cc}{e^{-2t}}&{0}\\
{0}&{e...
...
{-e^{-2t}+e^{-5t}}&{-e^{-2t}+4e^{-5t}}\end{array}\right] \ . \end{displaymath}](img2664.png)
![]() il vettor tangente alla curva
il vettor tangente alla curva ![]() è proporzionale ad un vettore ottenuto ruotando
è proporzionale ad un vettore ottenuto ruotando ![]() dell'angolo orientato
dell'angolo orientato ![]() , la curva
, la curva ![]() è soluzione del sistema dinamico
è soluzione del sistema dinamico
![\begin{displaymath}\dot X=AX\;,\;\mbox{ con } A=\alpha\left[\begin{array}{cc}{\c...
...\sin\omega}\\
{\sin\omega}&{\cos\omega}\end{array}\right]\ . \end{displaymath}](img2669.png)
![\begin{displaymath}X(t)=e^{At}X_0=e^{(\alpha\cos\omega)t} \left[\begin{array}{cc...
...omega)t]}&{\cos[(\alpha\sin\omega)t]}\end{array}\right]\,X_0\ .\end{displaymath}](img2672.png)
![\begin{displaymath}X(t)=\left[\begin{array}{cc}{\cos(\alpha t)}&{\mp\sin(\alpha t)}\\
{\pm\sin(\alpha t)}&{\cos(\alpha t)}\end{array}\right]X_0 \end{displaymath}](img2674.png)
![\begin{displaymath}V=\left[\begin{array}{cc}{\sqrt{3/2}}&{0}\\
{0}&{1}\end{arr...
...array}{cc}{2}&{-\sqrt{6}}\\
{\sqrt{6}}&{2}\end{array}\right] \end{displaymath}](img2681.png)
![\begin{displaymath}\exp(At)=V \; e^{2t}\; \left[\begin{array}{cc}{\cos(\sqrt{6}t...
...{\sin(\sqrt{6}t)}&{\cos(\sqrt{6}t)}\end{array}\right]\; V^{-1} \end{displaymath}](img2682.png)
![\begin{displaymath}V^{-1}\; A \; V= D=\left[\begin{array}{ccc}
{-1}&{0}&{0}\\ {0...
...{1}&{-1}&{1}\\ {1}&{0}&{-1}\\ {0}&{1}&{0}\end{array}\right]\;, \end{displaymath}](img2683.png)
![\begin{displaymath}e^{Dt}=\left[\begin{array}{ccc}
{e^{-t}}&{0}&{0}\\ {0}&{e^{4t...
...}\\ {0}&{e^{4t}\sin(3t)}&{e^{4t}\cos(3t)}\end{array}\right]\;. \end{displaymath}](img2684.png)
![]() ha diversi da zero solo quelli di posto
ha diversi da zero solo quelli di posto ![]() , se esistono; e così via. Quindi nell'esponenziale il coefficiente di posto
, se esistono; e così via. Quindi nell'esponenziale il coefficiente di posto ![]() sarà
sarà ![]() ; sulla diagonale
; sulla diagonale ![]() e sopra la diagonale principale
e sopra la diagonale principale ![]() .
.
![\begin{displaymath}D=\left[\begin{array}{cc}{-3}&{0}\\
{1}&{-3}\end{array}\rig...
...egin{array}{cc}{-1/2}&{-1}\\
{-1/4}&{0}\end{array}\right]\;. \end{displaymath}](img2690.png)
![\begin{displaymath}\left[\begin{array}{c}{y_1(t)}\\
{y_2(t)}\end{array}\right]...
...\left[\begin{array}{c}{y_1^0}\\
{y_2^0}\end{array}\right]\;, \end{displaymath}](img2692.png)
![]() e
e ![]() , dato che
, dato che
![]() . Se
. Se ![]() , anche
, anche ![]() ,
,
![]() e
e
![\begin{displaymath}A=\left[\begin{array}{cc}{a}&{b}\\
{-\frac{a^2}{b}}&{-a}\end{array}\right]\ ; \end{displaymath}](img2699.png)
![\begin{displaymath}A=\left[\begin{array}{cc}{0}&{b}\\
{0}&{0}\end{array}\right...
...y}{cc}{0}&{0}\\
{b}&{0}\end{array}\right]\;,\;b\in{\bf R}\;. \end{displaymath}](img2701.png)
![]() ha un solo autovalore
ha un solo autovalore ![]() , la matrice
, la matrice
![]() ha solo l'autovalore
ha solo l'autovalore ![]() e quindi ha traccia nulla:
e quindi ha traccia nulla:
![]() .
. ![]() di
di ![]() ha
ha ![]() blocchi di Jordan, dove
blocchi di Jordan, dove ![]() è la dimensione del
è la dimensione del ![]() . Dallo studio della caratteristica di
. Dallo studio della caratteristica di
![\begin{displaymath}(A-2I)= \left [\begin{array}{cccc} -2&-1&0&2\\ 6&4&2&-6\\ -3&-2&-1&3\\ 1&1&1&-1 \end{array}\right ]\end{displaymath}](img2706.png)
![\begin{displaymath}V_1=\left [\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right ]\;...
...;V_4=\left [\begin{array}{c}-1\\ 4\\ -2\\ 1\end{array}\right ] \end{displaymath}](img2714.png)
![\begin{displaymath}D= \left [\begin{array}{cccc} 2&0&0&0\\ 1&2&0&0\\ 0&0&2&0\\ 0...
...0&-1&-1\\ 0&0&-1&-2\\ 0&1&2&0\\ 0&0&1&3 \end{array}\right ]\;. \end{displaymath}](img2716.png)
![\begin{displaymath}X(t)=B^{-1}\left [\begin{array}{cccc} 2e^{2t}&0&0&0\\ te^{2t}...
...0&0&2e^{2t}&0\\ 0&0&te^{2t}&2e^{2t} \end{array}\right ]BX_0\;. \end{displaymath}](img2718.png)