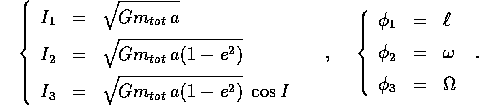 e le
loro masse con
e le
loro masse con  , la lagrangiana sarà
, la lagrangiana sarà
Sommario Il moto di corpi nello spazio è storicamente il problema intorno al quale si è sviluppata la meccanica moderna (ed anche gran parte della matematica moderna, come il calcolo differenziale). Nel caso in cui due soli corpi puntiformi interagiscono mediante una forza centrale, il problema è integrabile, perché possiede gli integrali del centro di massa, del momento angolare e dell'energia. Se in particolare la forza attrattiva è inversamente proporzionale al quadrato delle distanze, le orbite sono esprimibili come sezioni coniche, e le variabili azione-angolo sono calcolabili esplicitamente in termini finiti: i passaggi sono tutti esplicitamente analitici, ad eccezione di una inversione, l'equazione di Keplero.
Per problema dei due corpi intendiamo la descrizione del moto di due corpi puntiformi sotto l'azione della sole forze di interazione dei due corpi stessi, che si suppongono forze centrali per le quali valga la legge di azione e reazione .
Se indichiamo le posizioni dei due corpi con  e le
loro masse con
e le
loro masse con 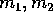 , la lagrangiana sarà
, la lagrangiana sarà
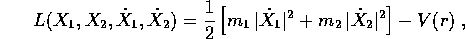
dove V è l'energia potenziale dell'interazione e
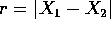 la distanza. Le equazioni di Lagrange
sono
la distanza. Le equazioni di Lagrange
sono
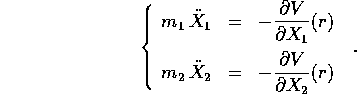
Questo problema appare complicato perché ha dimensionalità
elevata: in effetti è un sistema dinamico in 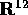 .
Tuttavia il sistema è integrabile nel senso del
teorema di Arnold-Jost , perché ha un numero
sufficiente di integrali primi .
Utilizzando questi
integrali primi, ridurremo gradualmente il problema fino
ad un solo grado di libertà.
.
Tuttavia il sistema è integrabile nel senso del
teorema di Arnold-Jost , perché ha un numero
sufficiente di integrali primi .
Utilizzando questi
integrali primi, ridurremo gradualmente il problema fino
ad un solo grado di libertà.
La prima riduzione del problema è resa possibile dalla legge di azione e reazione

che permette di ricavare per il centro di massa
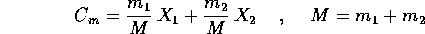
l'equazione di moto
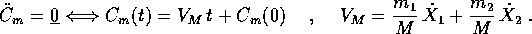
Perciò possiamo ridurre il problema ad un sistema
dinamico in 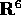 nel modo seguente. Consideriamo
il vettore di posizione relativa del secondo corpo rispetto al
primo, e ricaviamo le equazioni di moto per differenza: da
nel modo seguente. Consideriamo
il vettore di posizione relativa del secondo corpo rispetto al
primo, e ricaviamo le equazioni di moto per differenza: da
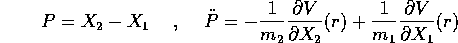
si ottiene
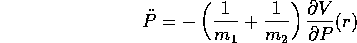
poiché le derivate parziali di V(r)
rispetto alle coordinate 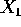 sono l'opposto di quelle
rispetto alle coordinate di
sono l'opposto di quelle
rispetto alle coordinate di 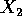 .
.
Una soluzione del sistema dinamico in 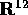 ,
con condizione iniziale
,
con condizione iniziale
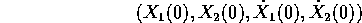
si otterrà a partire da una soluzione del sistema dinamico in 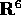 con condizioni iniziali
con condizioni iniziali 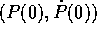 e da una soluzione
dell'equazione di moto del cento di massa: data la curva P(t) e dato
e da una soluzione
dell'equazione di moto del cento di massa: data la curva P(t) e dato
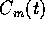 ,
,
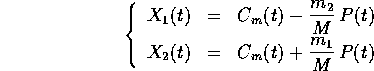
è la soluzione del problema originario.
La stessa riduzione si può derivare dal formalismo lagrangiano, considerando la trasformazione
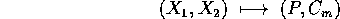
come un cambiamento di coordinate; per la
covarianza delle equazioni di Lagrange per
scrivere le equazioni di moto per 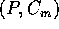 basta esprimere
la lagrangiana nelle nuove coordinate. Poiché
basta esprimere
la lagrangiana nelle nuove coordinate. Poiché
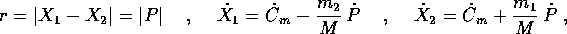
sostituendo nella lagrangiana originaria si ottiene
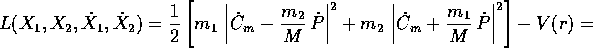
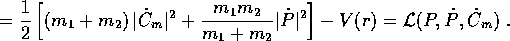
La lagrangiana nelle nuove coordinate non solo è ciclica nelle
coordinate di 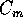 (onde gli integrali primi che sono i momenti
coniugati, cioè le componenti della
quantità di moto del baricentro
(onde gli integrali primi che sono i momenti
coniugati, cioè le componenti della
quantità di moto del baricentro
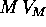 ), ma è somma di una funzione
della sola
), ma è somma di una funzione
della sola 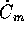 e di una funzione di
e di una funzione di 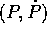 , perciò i
due gruppi di variabili hanno
dinamiche del tutto disaccoppiate.
Il
moto del centro di massa è governato dalla lagrangiana del moto
libero
, perciò i
due gruppi di variabili hanno
dinamiche del tutto disaccoppiate.
Il
moto del centro di massa è governato dalla lagrangiana del moto
libero
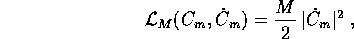
mentre il moto relativo è governato dalla lagrangiana ridotta
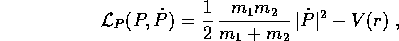
che è quella del problema della forza centrale in cui al corpo fittizio P è attribuita (dal formalismo lagrangiano) la massa ridotta , cioè la media armonica delle due masse:
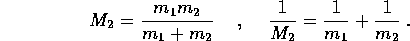
Poiché il fattore moltiplicativo 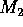 non influisce sulla
dinamica, si può considerare come lagrangiana ridotta
non influisce sulla
dinamica, si può considerare come lagrangiana ridotta
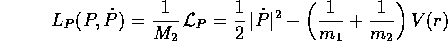
le cui equazioni di Lagrange sono esattamente le equazioni di moto per P che abbiamo ottenuto per differenza. Per semplificare la notazione indichiamo l'energia potenziale riscalata con W(r):
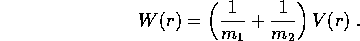
Poiché la lagrangiana del problema dei due corpi è simmetrica rispetto alle rotazioni, per il teorema di Noether le equazioni di moto avranno un vettore di integrali primi, che si può interpretare come momento angolare . Il momento angolare totale è, nel riferimento originario del problema dei due corpi,
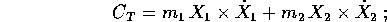
se si passa al riferimento  del moto relativo e del
centro di massa, e si applica alla lagrangiana
del moto relativo e del
centro di massa, e si applica alla lagrangiana  il teorema di Noether, si trova,
con formula del tutto simile, il vettore di integrali primi
il teorema di Noether, si trova,
con formula del tutto simile, il vettore di integrali primi
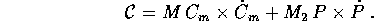
Il primo termine rappresenta il contributo del centro di massa
al momento angolare, il secondo è il momento angolare
calcolato in un riferimento avente l'origine in 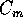 .
.
Si può verificare per sostituzione che 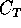 e
e
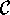 rappresentano lo stesso vettore, cioè
sono funzioni che si corrispondono per valore nei due sistemi
di riferimento. Questa proprietà, legata al fatto che nelle nuove
coordinate l'energia cinetica è ancora espressa per mezzo di
una matrice diagonale, si generalizza ad
un sistema di coordinate dette ``jacobiane'': cfr. [Milani-Nobili 83].
rappresentano lo stesso vettore, cioè
sono funzioni che si corrispondono per valore nei due sistemi
di riferimento. Questa proprietà, legata al fatto che nelle nuove
coordinate l'energia cinetica è ancora espressa per mezzo di
una matrice diagonale, si generalizza ad
un sistema di coordinate dette ``jacobiane'': cfr. [Milani-Nobili 83].
Facendo la consueta economia di termini e fattori costanti, possiamo considerare il momento angolare ridotto

e verificare che è un integrale primo:
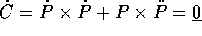 ,
dove il primo termine è identicamente nullo ed il secondo
si annulla perché l'accelerazione ha direzione
radiale. Ne segue che la posizione P(t) del moto relativo,
ed anche la velocità
,
dove il primo termine è identicamente nullo ed il secondo
si annulla perché l'accelerazione ha direzione
radiale. Ne segue che la posizione P(t) del moto relativo,
ed anche la velocità 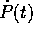 , giacciono per ogni t in
un piano perpendicolare al vettore momento angolare. Quindi, se
si sceglie un sistema di coordinate di
, giacciono per ogni t in
un piano perpendicolare al vettore momento angolare. Quindi, se
si sceglie un sistema di coordinate di 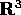 tale che l'asse
z sia lungo C (e con lo stesso verso), le equazioni di
moto relative alla coordinata z sono semplicemente
tale che l'asse
z sia lungo C (e con lo stesso verso), le equazioni di
moto relative alla coordinata z sono semplicemente 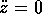 , ed hanno soluzione
, ed hanno soluzione 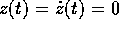 . Possiamo quindi
considerare
. Possiamo quindi
considerare 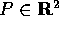 , ed il sistema dinamico in
, ed il sistema dinamico in 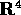 .
.
L'impiego dei tre integrali primi corrispondenti alle componenti
del momento angolare ha consentito di ridurre lo spazio delle fasi da
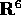 ad
ad 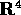 : poiché l'insieme invariante definito in
: poiché l'insieme invariante definito in
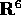 da tre equazioni indipendenti è una varietà di dimensione
3, si capisce che gli integrali del momento angolare non sono stati
ancora sfruttati in pieno. In effetti è stata utilizzata solo la
direzione del vettore C, non la sua lunghezza, che comparirà
ancora come integrale primo nel problema piano.
da tre equazioni indipendenti è una varietà di dimensione
3, si capisce che gli integrali del momento angolare non sono stati
ancora sfruttati in pieno. In effetti è stata utilizzata solo la
direzione del vettore C, non la sua lunghezza, che comparirà
ancora come integrale primo nel problema piano.
Per risolvere il problema ridotto al piano conviene passare alle
coordinate polari 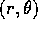 nel piano dell'orbita.
La lagrangiana si trasforma in
nel piano dell'orbita.
La lagrangiana si trasforma in
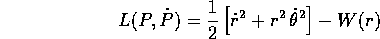
e si ottiene immediatamente un integrale primo, cioè il
momento 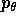 coniugato alla variabile ciclica
coniugato alla variabile ciclica 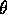
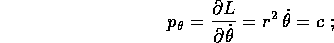
da qui si può ricavare 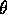 per quadratura , una volta che
sia noto r(t), usando
per quadratura , una volta che
sia noto r(t), usando

Questa formula va generalmente sotto il nome di
legge delle aree , o
seconda legge di Keplero : infatti la
costante 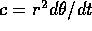 coincide (a meno del un fattore 2) con la
derivata rispetto al tempo dell'area ``spazzata dal raggio vettore",
cioè dell'area
coincide (a meno del un fattore 2) con la
derivata rispetto al tempo dell'area ``spazzata dal raggio vettore",
cioè dell'area
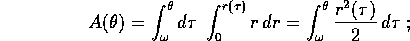
dunque le aree spazzate dal raggio vettore sono proporzionali ai tempi.
Sostituendo la costante c nella lagrangiana si ottiene la lagrangiana ad un grado di libertà:
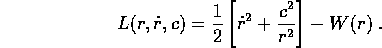
Per concludere sull'integrabilità del problema dei due corpi,
non resta che applicare la trasformazione di Legendre
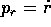 e trovare la hamiltoniana
e trovare la hamiltoniana
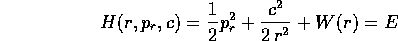
che fornisce l'ultimo integrale primo. Il problema dei due
corpi è dunque integrabile,
mediante quadrature ed inversioni (che
sono utilizzate per risolvere il sistema hamiltoniano ad un grado di
libertà, e per trovare la legge oraria  ) e
mediante espressioni analitiche esplicite (per
tutti gli altri passaggi).
) e
mediante espressioni analitiche esplicite (per
tutti gli altri passaggi).
Lo studio qualitativo delle soluzioni si ottiene dallo studio dell'energia potenziale effettiva
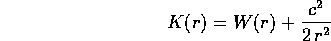
ed in particolare dalle proprietà degli insiemi dei valori di
r per cui 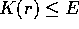 ; per esempio se si ottiene un
intervallo
; per esempio se si ottiene un
intervallo 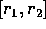 con
con 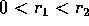 ne risultano orbite
limitate, che non vanno né all'infinito, né alla collisione
r=0.
ne risultano orbite
limitate, che non vanno né all'infinito, né alla collisione
r=0.
Facciamo ordine nell'insieme degli integrali primi del problema dei due
corpi. Dal problema ridotto si deduce
l'integrale dell'energia ridotta, che naturalmente è legato a
quello dell'energia totale 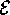 :
:
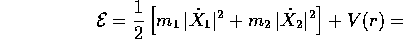
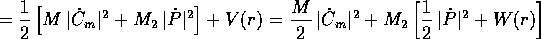
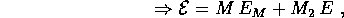
dove 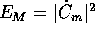 è l'energia del
moto libero del centro di massa ed E l'energia ridotta .
è l'energia del
moto libero del centro di massa ed E l'energia ridotta .
Anche l'integrale 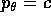 è legato al vettore momento
angolare: poiché infatti la componente
della velocità in direzione radiale non contribuisce
al momento angolare, e la componente trasversale è
è legato al vettore momento
angolare: poiché infatti la componente
della velocità in direzione radiale non contribuisce
al momento angolare, e la componente trasversale è
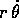 , si ha
, si ha
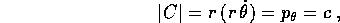
purché il sistema di riferimento sia stato scelto in modo
che 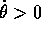 .
.
In conclusione, il problema dei due corpi ha sette integrali
indipendenti dal tempo: tre componenti della quantità di
moto, tre componenti del momento angolare, e l'energia totale.
Il teorema di Arnold-Jost non si può applicare
direttamente, perché gli insiemi di livello non sono
compatti (se la quantità di moto è diversa da 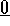 , le orbite sono illimitate); però i tre integrali della
quantità di moto possono essere impiegati per eliminare le
sei variabili
, le orbite sono illimitate); però i tre integrali della
quantità di moto possono essere impiegati per eliminare le
sei variabili 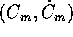 m, anche con l'aiuto dei tre
integrali primi dipendenti dal tempo
m, anche con l'aiuto dei tre
integrali primi dipendenti dal tempo 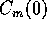 .
.
Il problema ridotto ha tre gradi di libertà e i quattro integrali E, C,
che tuttavia non sono in commutazione. Da questi si possono
estrarre tre integrali primi in commutazione: 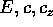 :
in primo luogo
:
in primo luogo
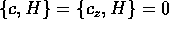 perché sono integrali primi; inoltre
con un calcolo non banale si può mostrare che
perché sono integrali primi; inoltre
con un calcolo non banale si può mostrare che 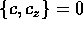 .
Infatti in coordinate polari sferiche
.
Infatti in coordinate polari sferiche 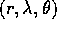
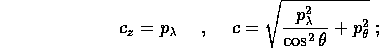
quindi la loro parentesi di Poisson è
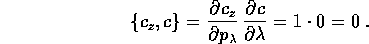
Perciò il sistema ridotto, con tre gradi di libertà e tre integrali in commutazione, è del tipo descritto dal teorema di Arnold-Jost ; resta da vedere dove i gradienti dei tre integrali primi sono indipendenti, e quali insiemi di livello sono compatti. Questo dipenderà dalla forma dell'energia potenziale W(r), e quindi dell'energia potenziale effettiva K(r).
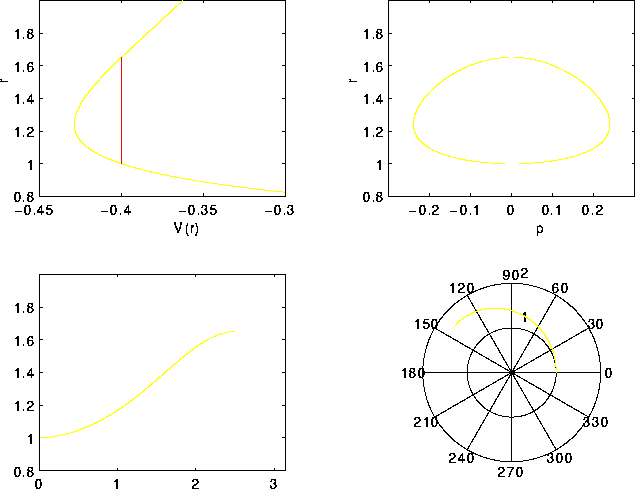
Figure 7.1: Le quattro figure mostrano: il potenziale
effettivo in funzione del raggio; una curva di livello dell'energia
nel piano del momento e della coordinata r; la traiettoria in
coordinate polari (raggio r ed angolo, ricavato per quadratura
rispetto alla variabile r); la traiettoria in coordinate cartesiane,
per il tratto compreso tra il raggio minimo e massimo. Si noti che
l'angolo tra la posizione al pericentro e quella all'apocentro non è
un angolo piatto: la traiettoria non si richiude al prossimo passaggio
al pericentro.
Se per esempio K(r) tende a 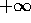 per
per  , per ogni valore
E dell'energia totale ci sarà un valore minimo
, per ogni valore
E dell'energia totale ci sarà un valore minimo  tale che
tale che
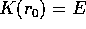 , mentre K(r)>E per
, mentre K(r)>E per 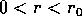 . Allora calcoliamo l'inversa
della legge oraria: risolvendo l'equazione dell'energia
. Allora calcoliamo l'inversa
della legge oraria: risolvendo l'equazione dell'energia 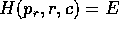 rispetto a
rispetto a 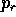 si trova
si trova
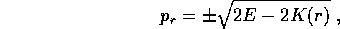
da cui, essendo 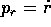 ,
,
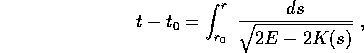
dove  è il tempo al quale l'orbita passa al pericentro (ovvero
dal punto in cui
è il tempo al quale l'orbita passa al pericentro (ovvero
dal punto in cui 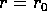 ).
).
Invece la dipendenza di 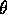 dal tempo si può ricavare da
un'altra quadratura : poiché
dal tempo si può ricavare da
un'altra quadratura : poiché 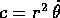 ,
,
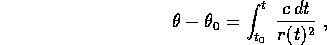
dove 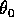 è l'argomento del pericentro (ovvero la direzione
del punto in cui
è l'argomento del pericentro (ovvero la direzione
del punto in cui 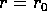 ). Se ci si limita ad un intervallo di valori
di t nel quale la relazione tra t ed r è monotona, allora si
può cambiare variabile nella quadratura sostituendo dt con
). Se ci si limita ad un intervallo di valori
di t nel quale la relazione tra t ed r è monotona, allora si
può cambiare variabile nella quadratura sostituendo dt con 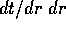 , ottenendo
, ottenendo
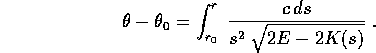
Se l'energia potenziale effettiva K(r) ha un punto stazionario
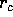 , in cui
, in cui 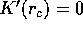 , allora esiste una soluzione con
, allora esiste una soluzione con 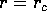 costante e
costante e 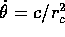 costante, cioè un'orbita
circolare; il valore del raggio
costante, cioè un'orbita
circolare; il valore del raggio 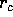 dell'orbita circolare dipende
solo dal valore del momento angolare c.
dell'orbita circolare dipende
solo dal valore del momento angolare c.
Infine, se l'energia potenziale W(r) tende a 0 per 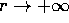 (come è ragionevole immaginare per un'interazione fisicamente possibile),
altrettanto fa l'energia potenziale effettiva K(r), e si
avranno due casi ben distinti:
(come è ragionevole immaginare per un'interazione fisicamente possibile),
altrettanto fa l'energia potenziale effettiva K(r), e si
avranno due casi ben distinti:
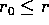 ) si
avrà un toro invariante per il teorema di Arnold-Jost. Dopo un giro,
quando cioè
) si
avrà un toro invariante per il teorema di Arnold-Jost. Dopo un giro,
quando cioè 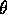 sarà aumentata di
sarà aumentata di 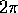 rispetto al valore
iniziale
rispetto al valore
iniziale 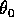 , il valore di r non sarà in generale tornato
al minimo
, il valore di r non sarà in generale tornato
al minimo 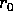 , e quindi la traiettoria descriverà una ``rosetta'',
cioè resterà confinata in una corona circolare, con raggi
corrispondenti al pericentro ed all'apocentro (punto con raggio
massimo). Secondo il valore del rapporto tra le due
frequenze proprie
del flusso di Kronecker sul toro invariante, le traiettorie
potranno richiudersi perché le corrispondenti orbite sono
periodiche, oppure riempire la corona circolare.
, e quindi la traiettoria descriverà una ``rosetta'',
cioè resterà confinata in una corona circolare, con raggi
corrispondenti al pericentro ed all'apocentro (punto con raggio
massimo). Secondo il valore del rapporto tra le due
frequenze proprie
del flusso di Kronecker sul toro invariante, le traiettorie
potranno richiudersi perché le corrispondenti orbite sono
periodiche, oppure riempire la corona circolare.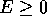 vi saranno orbite illimitate con
vi saranno orbite illimitate con 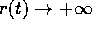 e
e 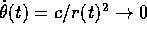 :
se anche
:
se anche 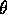 ha limite finito, c'è una ``direzione
di fuga'' in corrispondenza dell'asintoto.
ha limite finito, c'è una ``direzione
di fuga'' in corrispondenza dell'asintoto.
Il problema dei due corpi gravitazionale si ottiene specificando nel problema dei due corpi trattato fin qui la legge della forza proporzionale all'inverso del quadrato della distanza. Allora l'energia potenziale gravitazionale risulta
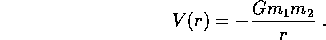
La proporzionalità dell'energia potenziale a entrambe le masse, e con una costante di proporzionalità G che è universale (cioè non dipende dalla composizione né da alcun altra proprietà dei corpi) deriva dall'equivalenza della massa inerziale con la massa sorgente del campo gravitazionale, ed è uno dei principi fondamentali della gravitazione newtoniana (e anche di quella einsteiniana).
L'energia potenziale riscalata è quindi
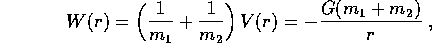
che corrisponde all'energia potenziale di un corpo di massa unitaria
nel campo gravitazionale di un corpo con massa pari alla
massa totale 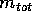 ; la hamiltoniana è
; la hamiltoniana è
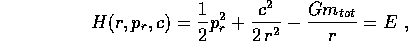
ed il momento coniugato ad r
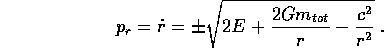
Allora la relazione tra 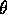 ed r si può ricavare dalla quadratura
ed r si può ricavare dalla quadratura
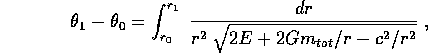
dove si intende che  corrisponde ad
corrisponde ad  .
I possibili valori
.
I possibili valori  del raggio al pericentro si possono ricavare dall'equazione
del raggio al pericentro si possono ricavare dall'equazione
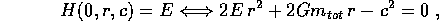
con soluzioni
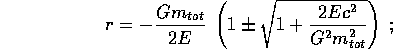
per E>0 le soluzioni sono reali e di segno discorde, per cui
esiste un pericentro 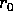 ma la traiettoria non è limitata; anche per
E=0 la soluzione è illimitata; per E<0, infine, le soluzioni sono
entrambe reali e positive purché
ma la traiettoria non è limitata; anche per
E=0 la soluzione è illimitata; per E<0, infine, le soluzioni sono
entrambe reali e positive purché
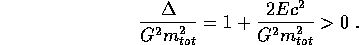
Poiché l'espressione qui sopra ricorrerà frequentemente, introduciamo la notazione
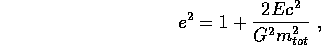
valida per 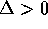 (cioè sempre se
(cioè sempre se 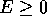 , e per valori
opportuni di c se E<0). La lettera e in questo capitolo non
indica il numero di Nepero, ma l'eccentricità
di Keplero, la cui interpretazione geometrica sarà chiara tra poco.
, e per valori
opportuni di c se E<0). La lettera e in questo capitolo non
indica il numero di Nepero, ma l'eccentricità
di Keplero, la cui interpretazione geometrica sarà chiara tra poco.
Limitiamoci quindi a considerare il caso 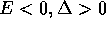 . La
quadratura che fornisce
. La
quadratura che fornisce 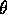 in funzione di r può essere
eseguita analiticamente, contenendo la radice di un polinomio di
secondo grado: sostituendo u=1/r come variabile di integrazione
in funzione di r può essere
eseguita analiticamente, contenendo la radice di un polinomio di
secondo grado: sostituendo u=1/r come variabile di integrazione
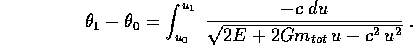
Il polinomio di secondo grado sotto radice ha radici reali perché il
suo discriminante è ancora lo stesso 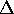 che abbiamo supposto
maggiore di zero. Perciò l'integrale si calcola con la sostituzione
che abbiamo supposto
maggiore di zero. Perciò l'integrale si calcola con la sostituzione
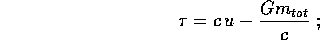
notando anche che il valore 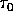 corrisponde ad
corrisponde ad 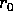 , dove la
radice si annulla, si ha che
, dove la
radice si annulla, si ha che
Figure 7.2: Le quattro figure mostrano, per il problema dei
due corpi gravitazionale: il potenziale effettivo in funzione del
raggio; una curva di livello dell'energia nel piano del momento e
della coordinata r; la traiettoria nel piano delle coordinate
polari, cioè l'angolo, ricavato per quadratura rispetto alla
variabile r, ed il raggio; la traiettoria in coordinate cartesiane,
per il tratto compreso tra il raggio minimo e massimo. L'angolo tra il
pericentro e l'apocentro è esattamente un angolo piatto (a meno del
piccolo errore introdotto nella quadratura numerica), quindi la
traiettoria si richiude al prossimo passaggio al pericentro e l'orbita
è periodica.
Invertendo l'arcocoseno, e ricordando le definizioni di  ed u,
si trova
ed u,
si trova
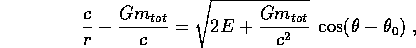
e, ricavando r in funzione di 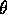 ,
,
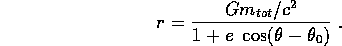
Questa formula vale per ogni valore degli integrali primi E e c,
purché non sia negativa l'espressione di 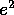 ,
e rappresenta la prima legge di Keplero :
le traiettorie del problema dei due corpi gravitazionale sono
sezioni coniche. Se infatti si considera un sistema di coordinate
tale che
,
e rappresenta la prima legge di Keplero :
le traiettorie del problema dei due corpi gravitazionale sono
sezioni coniche. Se infatti si considera un sistema di coordinate
tale che 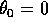 , ossia tale che l'asse x abbia la direzione del
pericentro e che l'asse y stia nel piano orbitale, troviamo
, ossia tale che l'asse x abbia la direzione del
pericentro e che l'asse y stia nel piano orbitale, troviamo
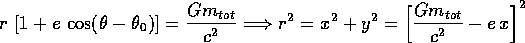
che è un'ellisse per 0<e<1, una parabola per e=1, una circonferenza per e=0, un'iperbole per e>1. In ogni caso, un fuoco è nell'origine; nel caso iperbolico la traiettoria occupa solo il ramo dell'iperbole più vicino al all'origine.
Le dimensioni delle sezioni coniche su cui giacciono le traiettorie si
possono dedurre dai valori minimi e massimi (se esistono) del raggio
r. Il minimo corrisponde a 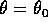 ; perciò l'angolo
; perciò l'angolo
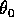 è l'argomento del pericentro e si indica
tradizionalmente con la lettera
è l'argomento del pericentro e si indica
tradizionalmente con la lettera 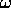 . Per e<1, il massimo corrisponde
per
. Per e<1, il massimo corrisponde
per 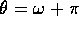 ; l'asse maggiore dell'ellisse è la somma del
raggio massimo con il raggio minimo
; l'asse maggiore dell'ellisse è la somma del
raggio massimo con il raggio minimo
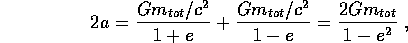
ovvero
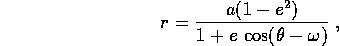
con distanza al pericentro a(1-e) e
all'apocentro a(1+e). La lunghezza a si chiama
semiasse maggiore dell'orbita ellittica. Il semiasse minore
dell'ellisse è 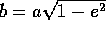 .
.
La formula che lega il momento angolare al semiasse maggiore
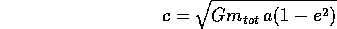
si può considerare valida anche nel caso iperbolico, pur di
ammettere valori negativi per a. Nel caso
parabolico non si può definire un semiasse maggiore, e si usa il
parametro 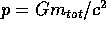 che corrisponde al doppio della distanza
al pericentro.
che corrisponde al doppio della distanza
al pericentro.
Un'altra relazione importante è quella tra energia e semiasse maggiore. Sostituendo la formula per c in funzione di a,e dentro la formula dell'eccentricità in funzione di E,c, si ricava
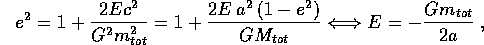
per cui l'integrale dell'energia dipende solo dal semiasse maggiore, e viceversa.
Per E<0, e 0<e<1, cioè per le orbite ellittiche, il raggio ha
valore massimo ed uno minimo, che sono le due radici (reali
e positive) di H(0,r,c)=E. Nel passare dal minimo al massimo di r,
l'angolo 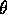 aumenta di esattamente
aumenta di esattamente  (perché coincide con
l'integrale dell'arcoseno sull'intero intervallo su cui la radice è
(perché coincide con
l'integrale dell'arcoseno sull'intero intervallo su cui la radice è
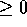 ). Quando l'orbita ritorna di nuovo al valore minimo di r,
l'angolo
). Quando l'orbita ritorna di nuovo al valore minimo di r,
l'angolo 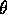 è aumentato di
è aumentato di 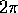 , per cui l'orbita passa da
, per cui l'orbita passa da
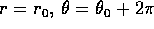 , cioè dallo stesso punto. In tale
punto i valori delle derivate sono determinati dagli integrali primi
E,c: infatti
, cioè dallo stesso punto. In tale
punto i valori delle derivate sono determinati dagli integrali primi
E,c: infatti 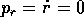 e
e 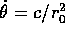 , perciò la
soluzione ripassa dalla stessa condizione iniziale ed è
un'orbita periodica . Quindi tutte le condizioni iniziali con
E<0 (un aperto nello spazio delle fasi) corrispondono ad orbite
periodiche.
, perciò la
soluzione ripassa dalla stessa condizione iniziale ed è
un'orbita periodica . Quindi tutte le condizioni iniziali con
E<0 (un aperto nello spazio delle fasi) corrispondono ad orbite
periodiche.
Per comprendere l'eccezionalità di questo risultato, si può
citare il teorema di Bertrand , per il quale i soli sistemi
governati da forze centrali con energia potenziale V(r) analitica
reale, per i quali esistano orbite periodiche che riempiono un aperto
nello spazio delle fasi, sono o oscillatori armonici con
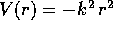 o modelli del problema dei due corpi gravitazionale
con
o modelli del problema dei due corpi gravitazionale
con 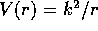 . Per un cenno di dimostrazione del teorema di
Bertrand si veda [Arnold 86], Capitolo 2.
. Per un cenno di dimostrazione del teorema di
Bertrand si veda [Arnold 86], Capitolo 2.
Per calcolare il periodo delle orbite ellittiche, si può utilizzare
la legge delle aree: l'area A spazzata dal raggio vettore
durante un intervallo di tempo pari ad un periodo P è l'area
dell'ellisse 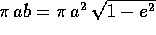
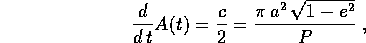
da cui, usando la relazione tra c ed a,e, si ricava la terza legge di Keplero :

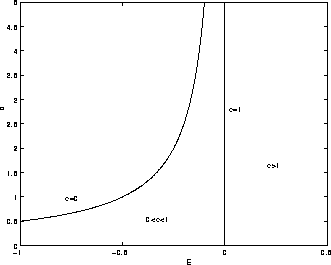
Figure 7.3: Nel piano (E,c) le orbite circolari stanno
sulla curva che fa da frontiera tra la regione
dove non è soddisfatta la condizione di realtà (per cui non ci
sono soluzioni con quei valori di E,c) e quella delle orbite
ellittiche; le orbite paraboliche E=0 separano le orbite ellittiche
da quelle iperboliche. Dal punto di vista del teorema di Arnold-Jost,
per E<0 ma e>0 si hanno dei tori invarianti perché le soluzioni
hanno raggi limitati sia dal di sopra che dal di sotto, per e=0 i
tori invarianti degenerano in circonferenze e per E non negativa le
soluzioni sono illimitate e le varietà invarianti sono cilindri. Il
caso c=0 corrisponde ad orbite con collisioni, e va trattato a
parte.
La frequenza propria è il moto medio

Si noti che il periodo (quindi anche il moto medio) non dipende dall'eccentricità. Poiché il semiasse maggiore dipende solo dall'energia, anche il periodo dipende solo dall'integrale dell'energia, non da quello del momento angolare.
Per descrivere le soluzioni del problema dei due corpi in 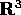 conviene introdurre il vettore di Laplace-Lenz
conviene introdurre il vettore di Laplace-Lenz
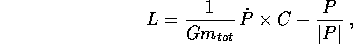
dove 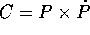 è il vettore momento angolare ridotto, in
coordinate relative
è il vettore momento angolare ridotto, in
coordinate relative 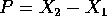 . Il secondo addendo è il versore
radiale
. Il secondo addendo è il versore
radiale 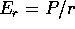 ; se usiamo il sistema di riferimento ortonormale
mobile definito da
; se usiamo il sistema di riferimento ortonormale
mobile definito da 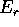 ,
, 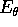 nel piano orbitale ed
nel piano orbitale ed 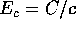 (con l'orientazione di
(con l'orientazione di 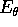 tale che
tale che 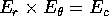 ),
valgono le seguenti regole di derivazione:
),
valgono le seguenti regole di derivazione:
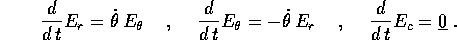
Possiamo quindi calcolare la derivata totale del vettore di Laplace-Lenz
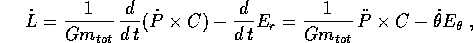
e, sostituendo l'espressione dell'accelerazione in funzione inversamente
proporzionale al quadrato della distanza, oltre che la formula
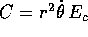 , si ottiene
, si ottiene
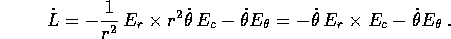
Poiché  , la derivata totale è nulla: quindi
le tre componenti del vettore di Laplace-Lenz sono integrali primi del moto.
L'interpretazione geometrica di questo vettore di integrali primi è semplice:
chiamiamo anomalia vera f l'angolo tra L e P (visto da C),
per il quale vale
, la derivata totale è nulla: quindi
le tre componenti del vettore di Laplace-Lenz sono integrali primi del moto.
L'interpretazione geometrica di questo vettore di integrali primi è semplice:
chiamiamo anomalia vera f l'angolo tra L e P (visto da C),
per il quale vale
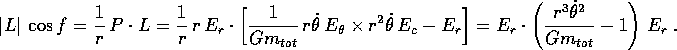
Allora
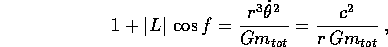
ed il confronto con la formula del raggio in funzione dell'angolo nel
piano orbitale consente di concludere che |L|=e ed
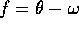 , ossia il vettore di Laplace-Lenz giace nel piano
orbitale, indica la direzione del pericentro ed ha lunghezza pari
all'eccentricità .
, ossia il vettore di Laplace-Lenz giace nel piano
orbitale, indica la direzione del pericentro ed ha lunghezza pari
all'eccentricità .
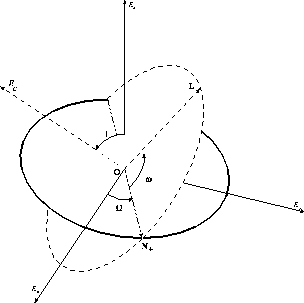
Figure 7.4: Degli elementi orbitali che descrivono un'orbita
kepleriana, tre sono angoli di Eulero che descrivono
l'orientazione nello spazio, mentre semiasse maggiore ed
eccentricità descrivono la forma e le dimensioni della traiettoria.
Un'orbita del problema dei due corpi (ridotto al moto relativo) sarà descritta da tre angoli:
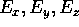 , per la quale
, per la quale

lo spigolo dell'angolo diedro formato dal piano (x,y) e dal piano orbitale avrà come versore

che indica la direzione del nodo ascendente , il punto in cui l'orbita attraversa da sotto a sopra il piano (x,y).
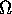 , longitudine del nodo ascendente, ovvero
l'angolo tra il nodo ascendente e l'asse x:
, longitudine del nodo ascendente, ovvero
l'angolo tra il nodo ascendente e l'asse x:
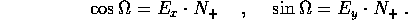
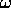 , argomento del pericentro , ovvero l'angolo
tra il nodo ascendente
, argomento del pericentro , ovvero l'angolo
tra il nodo ascendente 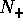 ed il vettore di Laplace-Lenz:
ed il vettore di Laplace-Lenz:
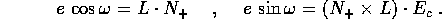
In definitiva, l'orbita viene individuata da sei
elementi orbitali : gli angoli di Eulero
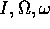 , gli elementi a,e e
l'angolo f; i primi 5 sono indipendenti dal tempo, cioè sono tutti
integrali primi, mentre f=f(t) può essere calcolato per quadratura
da
, gli elementi a,e e
l'angolo f; i primi 5 sono indipendenti dal tempo, cioè sono tutti
integrali primi, mentre f=f(t) può essere calcolato per quadratura
da 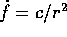 .
.
Il problema dei due corpi gravitazionale, ridotto al moto relativo, ha
tre gradi di libertà e tre integrali primi in commutazione 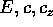 . Usiamo le coordinate polari sferiche per calcolare
questi tre integrali: l'integrale dell'energia ridotta è la hamiltoniana
(per unità di massa)
. Usiamo le coordinate polari sferiche per calcolare
questi tre integrali: l'integrale dell'energia ridotta è la hamiltoniana
(per unità di massa)
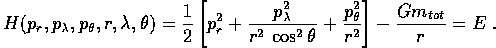
La componente z del momento angolare in queste coordinate è semplicemente
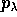 , mentre il momento angolare scalare è
, mentre il momento angolare scalare è
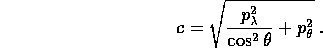
Usando queste espressioni possiamo verificare le ipotesi del teorema di Arnold-Jost . I gradienti di questi integrali primi sono
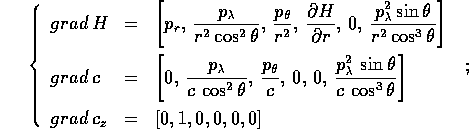
affinché siano linearmente indipendenti basta imporre che non accada
mai simultaneamente che 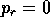 e
e 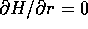 (per evitare
che
(per evitare
che 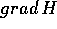 sia parallelo a
sia parallelo a 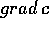 , e anche a
, e anche a  ) e
che non sia mai simultaneamente
) e
che non sia mai simultaneamente 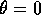 e
e 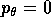 (per evitare che
(per evitare che
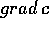 sia parallelo a
sia parallelo a  ).
).
Poiché 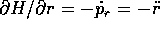 , la condizione
, la condizione
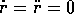 può verificarsi solo per un'orbita circolare.
La condizione
può verificarsi solo per un'orbita circolare.
La condizione 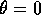 accompagnata da
accompagnata da 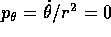 implica che
implica che 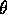 sia sempre 0, cioè che sia nulla l'inclinazione I; in
questo caso si avrebbe
sia sempre 0, cioè che sia nulla l'inclinazione I; in
questo caso si avrebbe 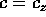 . Perciò, per orbite con I> 0 e con
e>0 i tre gradienti sono linearmente indipendenti, cioè i tre
integrali sono funzionalmente indipendenti.
. Perciò, per orbite con I> 0 e con
e>0 i tre gradienti sono linearmente indipendenti, cioè i tre
integrali sono funzionalmente indipendenti.
Anche la condizione di compattezza è facile da verificare.
Consideriamo l'insieme di livello 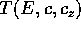 nello spazio delle fasi
di coordinate
nello spazio delle fasi
di coordinate 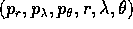 ; non
dimentichiamo che
; non
dimentichiamo che 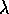 è una variabile angolo, e che
è una variabile angolo, e che 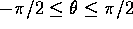 , per cui
, per cui 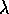 e
e 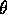 sono sempre
limitate. H è una forma quadratica definita positiva nei momenti,
quindi ciascuno di essi è limitato su H=E e quindi su
sono sempre
limitate. H è una forma quadratica definita positiva nei momenti,
quindi ciascuno di essi è limitato su H=E e quindi su
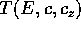 . Se il momento angolare c è diverso da zero, allora
il raggio r non può annullarsi; si tratta di verificare se il
raggio è limitato, e se questo è vero, allora l'insieme
. Se il momento angolare c è diverso da zero, allora
il raggio r non può annullarsi; si tratta di verificare se il
raggio è limitato, e se questo è vero, allora l'insieme 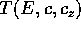 è limitato e chiuso , quindi compatto .
è limitato e chiuso , quindi compatto .
Dall'integrale dell'energia H=E, considerando anche fissato il
valore del momento angolare scalare c, si trova l'equazione per il
momento 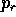
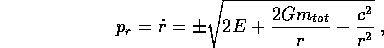
che, come abbiamo già visto, ha soluzioni per r compreso tra un
massimo ed un minimo quando E<0: in effetti 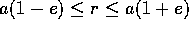 , dove a,e sono funzioni di E,c.
, dove a,e sono funzioni di E,c.
Consideriamo allora il dominio di Delaunay , che è l'aperto dello spazio delle fasi in cui E<0, I>0, e>0. Nel dominio di Delaunay valgono, per il problema dei due corpi gravitazionale, tutte le ipotesi del teorema di Arnold-Jost, quindi esistono delle variabili azione-angolo
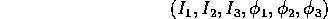
tali che ogni insieme di livello 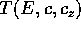 è un toro a
tre dimensioni
è un toro a
tre dimensioni 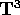 , su cui le azioni
, su cui le azioni 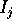 sono costanti, e gli
angoli
sono costanti, e gli
angoli 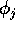 forniscono una carta coordinata.
forniscono una carta coordinata.
Si potrebbero usare gli integrali di linea della dimostrazione del teorema di Arnold-Jost per trovare l'espressione delle variabili azione; i calcoli relativi sarebbero molto simili a quelli già fatti nella Sezione 6.5 per integrare il problema della forza centrale mediante separazione di variabili nell'equazione di Hamilton-Jacobi . Poiché però conosciamo già la soluzione del problema dei due corpi, e la sua descrizione mediante elementi orbitali, possiamo procedere in modo più rapido. Possiamo dedurre direttamente dalle proprietà delle variabili azione-angolo le relazioni tra queste e gli elementi orbitali.
Poiché 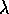 è una variabile ciclica,
è una variabile ciclica, 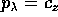 può
essere scelta come una delle variabili azione, supponiamo che sia
può
essere scelta come una delle variabili azione, supponiamo che sia
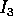 . La relazione di commutazione
. La relazione di commutazione
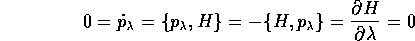
indica che 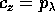 è l'integrale primo associato, per il
teorema di Noether , al gruppo di simmetrie che si ottiene
ruotando attorno all'asse z. Tra gli elementi orbitali, la
longitudine del nodo
è l'integrale primo associato, per il
teorema di Noether , al gruppo di simmetrie che si ottiene
ruotando attorno all'asse z. Tra gli elementi orbitali, la
longitudine del nodo 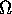 ha la proprietà che una traslazione
lungo l'asse
ha la proprietà che una traslazione
lungo l'asse 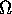 corrisponde ad una rotazione dell'orbita attorno
all'asse z. Quindi
corrisponde ad una rotazione dell'orbita attorno
all'asse z. Quindi 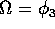 è la variabile coniugata ad
è la variabile coniugata ad
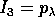 .
.
Lo stesso ragionamento applicato all'integrale c conduce a scegliere
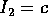 e ad individuare come variabile angolo coniugata l'argomento
del pericentro
e ad individuare come variabile angolo coniugata l'argomento
del pericentro 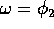 ; infatti
; infatti
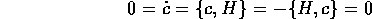
indica che la hamiltoniana è invariante rispetto a rotazioni nel
piano orbitale, cioè con asse C. Tali rotazioni sono realizzate
traslando lungo l'asse 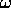 , cioè ruotando l'ellisse con
direzione del pericentro controllata da
, cioè ruotando l'ellisse con
direzione del pericentro controllata da 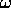 .
.
Resta da identificare la coppia di variabili azione-angolo 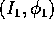 . La hamiltoniana come funzione delle variabili azione-angolo
non soltanto non dipende dalle
. La hamiltoniana come funzione delle variabili azione-angolo
non soltanto non dipende dalle 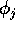 , ma dipende soltanto da
, ma dipende soltanto da 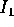 :
infatti
:
infatti 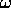 ed
ed 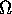 sono costanti, e le relative frequenze
proprie sono nulle:
sono costanti, e le relative frequenze
proprie sono nulle:
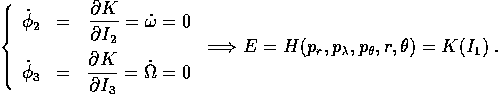
Allora la frequenza propria relativa all'angolo 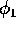 sarà
sarà
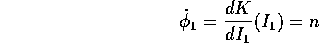
ed il periodo dell'orbita periodica sarà 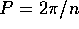 . Qui n=n(E) è il
moto medio , la cui dipendenza dal semiasse maggiore - e
quindi anche dall'energia - ci è nota dalla
terza legge di Keplero :
. Qui n=n(E) è il
moto medio , la cui dipendenza dal semiasse maggiore - e
quindi anche dall'energia - ci è nota dalla
terza legge di Keplero :
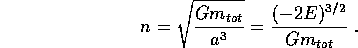
Eguagliando queste due espressioni di n, si ottiene l'equazione
differenziale a variabili separabili per la funzione 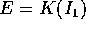
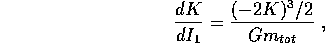
la cui soluzione è
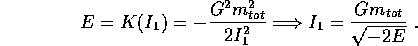
Quanto alla variabile 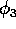 , sappiamo solo che è un angolo e che
cambia con il tempo in modo lineare, con frequenza n; poiché
possiamo scegliere un'origine arbitraria sull'asse
, sappiamo solo che è un angolo e che
cambia con il tempo in modo lineare, con frequenza n; poiché
possiamo scegliere un'origine arbitraria sull'asse 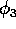 , possiamo
imporre che
, possiamo
imporre che 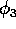 coincida con l'anomalia media , un angolo
coincida con l'anomalia media , un angolo  che coincide con l'anomalia vera al pericentro (cioè quando
vale 0, e per ragioni di simmetria anche quando vale
che coincide con l'anomalia vera al pericentro (cioè quando
vale 0, e per ragioni di simmetria anche quando vale  ) ma che
cambia linearmente con il tempo, in modo da avere lo stesso periodo.
) ma che
cambia linearmente con il tempo, in modo da avere lo stesso periodo.
In conclusione si possono costruire come variabili azione-angolo del problema dei tre corpi gravitazionale le variabili di Delaunay , le cui espressioni in funzione degli elementi orbitali sono le seguenti: