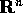
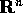
Le nozioni di topologia utilizzate in questo corso si
riferiscono soltanto agli insiemi 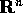ed ai loro
sottoinsiemi. In questo ambito, basta sapere che
le palle di raggio 
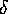
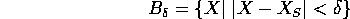
formano un sistema fondamentale di intorni del punto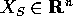 
che definisce la topologia, cioè gli insiemi aperti di
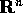, che sono tutte e sole le unioni degli intorni di tutti i
punti.
Teorema di equivalenza delle norme :
Se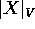 
è un'altra norma per i vettori 
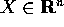, le
palle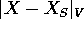 
definiscono la stessa topologia, cioè gli stessi
aperti.
Le nozioni di limite e di continuità di una funzione dipendono solo
dalla topologia, quindi sono indipendenti dalla scelta di una norma
negli spazi .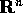
Il complementare di un aperto è un chiuso ; un insieme C tale
che ogni successione di suoi punti, e che ammette limite, ha limite
pure appartenente a C, è un chiuso. Un insieme K tale che ogni
successione di suoi punti ammette un valore limite pure appartenente a
K (cioè ha una sottosuccessione convergente ad un punto di K)
è un compatto ; esiste un'altra definizione di compatto (basata
sui ricoprimenti), ma nel contesto che ci interessa le due definizioni
sono equivalenti. Un insieme è compatto se e solo se è limitato e
chiuso. Ogni intervallo limitato e chiuso è un compatto di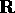 
;
quindi ogni successione limitata di numeri reali ha un minimo
limite , che è il più piccolo dei valori tali che esistono
sottosuccessioni con quel limite.
Un omeomorfismo è un'applicazione biunivoca, continua, e con inverso continuo; due insiemi omeomorfi hanno a comune tutte le proprietà che dipendono solo dalla topologia (ma non necessariamente proprietà metriche, come il volume).
La frontiera di un insieme C è l'insieme dei i punti tali che tutti i loro intorni contengono sia punti di C che punti non in C. Un chiuso contiene tutti i suoi punti di frontiera, un aperto non ne contiene nessuno.
Benché il punto all'infinito non appartenga ad 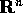, è sempre
legittimo parlare di limite infinito di una successione o
funzione a valori in 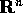, pur di considerare che gli insiemi
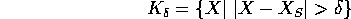
siano un sistema fondamentale di intorni del punto all'infinito.
Un insieme C è connesso se non si può scomporre in due
insiemi non vuoti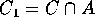 
e 
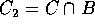con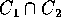 
vuoto, A, B aperti. Se al contrario una tale scomposizione è
possibile, i più grandi insiemi connessi contenuti in C si dicono
le sue componenti connesse .
Teorema della curva di Jordan :
Se C è l'immagine di una curva continua, semplice e chiusa, in
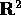, allora il complementare di C in 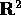ha esattamente due
componenti connesse, una (l'interno ) limitata, una
(l'esterno ) illimitata, tali che C fa da frontiera ad
entrambe.
Una varietà topologica di
dimensione n è un insieme V dotato di una topologia,
cioè di sottoinsiemi aperti, tali che per ogni punto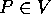 
esiste
un aperto W con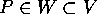 
, ed una carta coordinata ,
che è un omeomorfismo tra un aperto U di 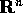e W.
Inoltre due carte coordinate, dove le loro immagini in V si
sovrappongono, differiscono per un omeomorfismo.
In realtà, per evitare esempi patologici, occorre che sia soddisfatta una condizione sulla topologia di V, l'assioma di separazione di Haussdorf.
Si parla di varietà differenziabile di clas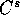se 
quando due carte
coordinate, dove le immagini in V
si sovrappongono, differiscono per un diffeomorfismo di classe .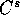
Per esempio, in dimensione 1 esistono solo due varietà (sia
topologiche che differenziabili) ``diverse'' (non ottenibili l'una
dall'altra con un omeomorfismo): la retta 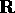e la circonferenza
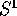. Al contrario in dimensione 2 vi sono molte varietà diverse:
quelle che sono anche compatte sono
classificate mediante una
proprietà topologica,
la caratteristica di Eulero-Poincaré : la sfera ha
caratteristica 2, il toro ha caratteristica zero, eccetera.
In pratica in questo corso non abbiamo bisogno di considerare le
varietà in astratto, ma solo le sotto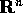varietà di . Per il teorema delle
funzioni implicite , si possono descrivere
le sottovarietà di 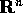come
luogo di punti definiti da equazioni F(X)=C con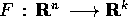 
, dove F è di classe 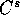e con jacobiana di
rango massimo ovunque (o almeno nell'intorno dei punti che soddisfano
alle equazioni).
Una varietà differenziabile V di dimensione n è dotata di un
fibrato tangente , composto da una copia dello spazio 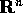per
ogni punto P di V; i vettori tangenti che vi appartengono possono
essere rappresentati, in una carta coordinata, dalla coppia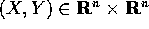 
, ma il vettore Y cambia in modo
controvariante al cambiare della carta coordinata.
Nel caso di una sottovarietà di 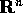, lo spazio vettoriale
immagine del differenziale della carta coordinata è lo
spazio tangente in ogni punto.
Lo spazio tangente in un punto
è formato dalle velocità delle curve che giacciono sulla
sottovarietà e passano per il punto.
Per le superfici, un campo vettoriale tangente ha un numero di punti
in cui si annulla non inferiore alla caratteristica di
Eulero-Poincaré. Una sottovarietà di 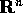, per esempio una
curva, oppure una superficie in 
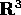, è dotata anche di
proprietà ``metriche''. Per esempio esiste una
prima forma fondamentale ,
che è una forma quadratica definita su ciascuno
spazio tangente, che assegna la lunghezza dei vettori velocità in
quel punto, quando i vettori velocità siano espressi come derivate
delle coordinate di una carta.
La seconda forma fondamentale esprime invece la curvatura della superficie, e quindi delle curve che giacciono su di essa.
L'energia cinetica di un moto vincolato è proporzionale alla prima forma fondamentale. invece la conoscenza della seconda forma fondamentale non è necessaria per scrivere le equazioni di moto, ma solo per calcolare l'intensità delle reazioni vincolari .
Bibliografia :