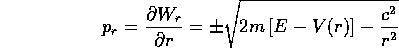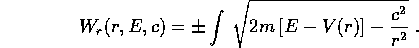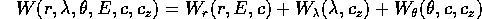



Next: 6.6 INTEGRABILITÀ
Up: 6 SISTEMI CONSERVATIVI: PIÙ
Previous: 6.4 SIMMETRIEINTEGRALI PRIMI
Sommario I sistemi hamiltoniani trattano sullo stesso piano
le coordinate ed i momenti; perciò è possibile utilizzare
dei cambiamenti di coordinate che mescolano le une e gli
altri. Se il cambiamento di carta nello spazio delle fasi
soddisfa opportune condizioni sulla matrice jacobiana, allora
è canonico, cioè conserva la forma delle equazioni di
Hamilton. Trasformazioni canoniche possono essere costruite a
partire da funzioni generatrici in variabili miste; questo
permette di cercare trasformazioni che semplificano
le equazioni di moto.
Definizione:
Più in generale le Q potrebbero essere le coordinate di una
carta locale di uno spazio delle configurazioni definito da vincoli
olonomi; in tal caso le P cambiano, nel passaggio da una carta
all'altra, in modo covariante , cioè come i gradienti e come
le equazioni di Lagrange: se le coordinate nella nuova carta sono Z
ed i momenti W
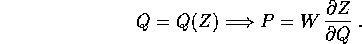
Vogliamo determinare quali cambiamenti di coordinate
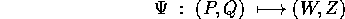
mandano le equazioni di Hamilton con hamiltoniana H(P,Q) nelle
equazioni di Hamilton con hamiltoniana K(W,Z) che è ottenuta per
composizione, cioè che corrisponde per valore :
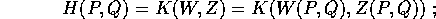
in tal caso il cambiamento di coordinate 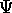 si dice una
trasformazione canonica .
si dice una
trasformazione canonica .
Teorema delle trasformazioni canoniche :
Sia 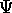 un cambiamento di coordinate che sia un diffeomorfismo
(
un cambiamento di coordinate che sia un diffeomorfismo
( 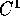 e con inversa
e con inversa 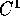 ); se A è la matrice jacobiana di
); se A è la matrice jacobiana di
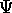 :
:
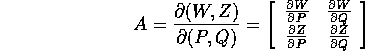
la trasformazione 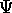 è canonica se e solo se
identicamente in ogni punto:
è canonica se e solo se
identicamente in ogni punto:

dove la matrice J è la matrice 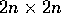

ottenuta accostando matrici zero e  matrici indentità
di tipo
matrici indentità
di tipo 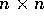 .
.
Si dice in tal caso che la matrice jacobiana A è una
matrice simplettica . La matrice J che definisce la
struttura simplettica dello spazio delle fasi di
dimensione 2n è evidentemente una generalizzazione della
matrice che definisce la struttura complessa del piano
(p,q) nel caso ad un solo grado di libertà; infatti è
sempre vero che 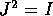 . Se si tiene a mente questa analogia,
sia l'enunciato che la dimostrazione di questo teorema sono
formalmente identici a quello del teorema delle
trasformazioni che conservano l'area .
. Se si tiene a mente questa analogia,
sia l'enunciato che la dimostrazione di questo teorema sono
formalmente identici a quello del teorema delle
trasformazioni che conservano l'area .
Dimostrazione:
-
-
Scriviamo le equazioni di Hamilton in forma vettoriale: nelle coordinate
(P,Q) e con hamiltoniana H(P,Q), e nelle coordinate (W,Z) e con hamiltoniana
K(W,Z):
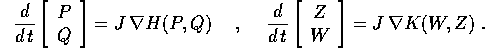
Calcoliamo la velocità nello spazio (W,Z) considerando le coordinate (W,Z)
come funzione delle (P,Q):
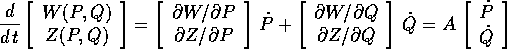
e sostituiamo al posto di 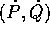 il secondo membro delle
equazioni di Hamilton nelle variabili (P,Q):
il secondo membro delle
equazioni di Hamilton nelle variabili (P,Q):
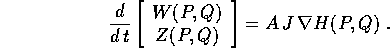
Ora si tratta di stabilire che relazione esiste tra il gradiente
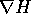 e quello
e quello 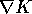 ; se facciamo l'ipotesi che le due
funzioni si corrispondano per valore, utilizzando il differenziale
della funzione composta:
; se facciamo l'ipotesi che le due
funzioni si corrispondano per valore, utilizzando il differenziale
della funzione composta:
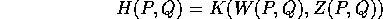
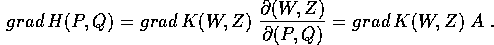
Per sostituire nell'equazione precedente occorre tenere presente che
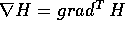
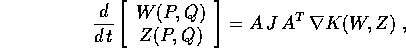
sempre sottintendendo che i punti (P,Q) e (W,Z) si corrispondano
per 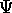 . Allora i due sistemi di equazioni di Hamilton si
corrispondono in ogni punto se e solo se vale identicamente:
. Allora i due sistemi di equazioni di Hamilton si
corrispondono in ogni punto se e solo se vale identicamente:

C.D.D.Esercizio
Verificare che sono trasformazioni canoniche le seguenti:
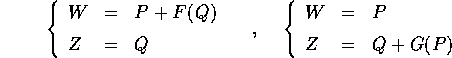
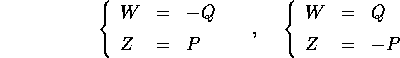
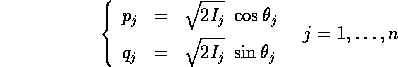
Teorema di Liouville :
Se A è una matrice simplettica, cioè
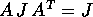 , allora valgono le seguenti
proprietà:
, allora valgono le seguenti
proprietà:

se 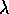 è un autovalore di A, anche
è un autovalore di A, anche 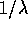 lo
è; sono gli stessi sia la molteplicità dell'autovalore , sia il
numero di blocchi di Jordan ).
lo
è; sono gli stessi sia la molteplicità dell'autovalore , sia il
numero di blocchi di Jordan ).
Poiché il determinante jacobiano appare nella formula di
cambiamento di variabile negli integrali multipli , se un
diffeomorfismo ha per matrice jacobiana una matrice simplettica allora
conserva il volume. Quindi le trasformazioni canoniche conservano il
volume dello spazio delle fasi.
Dimostrazione:
C.D.D.
Abbiamo visto come verificare che una data trasformazione è
canonica, mediante la matrice jacobiana. Cerchiamo un metodo per
costruire trasformazioni canoniche. Il procedimento è del
tutto analogo a quello della funzione generatrice ad un grado di libertà.
Teorema della funzione generatrice :
Sia B un insieme aperto dello spazio delle fasi con carta (P,Q), e sia
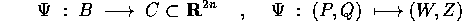
un diffeomorfismo di classe 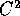 tra i due insiemi B e C, che
sia anche una trasformazione canonica.
tra i due insiemi B e C, che
sia anche una trasformazione canonica.
Sia 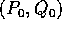 un punto di B tale che
un punto di B tale che 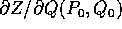 è una matrice invertibile.
Allora esiste un intorno U di
è una matrice invertibile.
Allora esiste un intorno U di 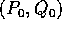 su
cui la
su
cui la 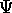 può essere descritta come segue: esiste una funzione F,
di classe
può essere descritta come segue: esiste una funzione F,
di classe 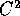 , delle variabili (Q,W), detta
funzione generatrice , il cui differenziale è:
, delle variabili (Q,W), detta
funzione generatrice , il cui differenziale è:
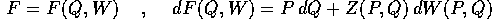
ossia, in termini di derivate parziali
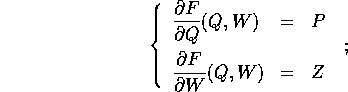
inoltre la funzione F(Q,W) ha la proprietà che
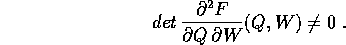
L'insieme di definizione di S(Q,W) è grande ``quanto è
necessario'' per definire la trasformazione tra tutti i punti di U
e tutti i punti di 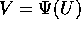 .
.
La dimostrazione che segue è simile a quella del teorema della
funzione generatrice . La sola
difficoltà aggiuntiva sta nel maneggiare la nozione di
forma differenziale lineare
a 2n variabili:
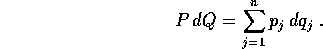
In particolare va utilizzata la nozione di
forma chiusa , ed il teorema di
Poincaré .
Dimostrazione:
-
-
Consideriamo la forma differenziale
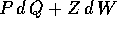 in funzione
delle variabili (Q,W). Poiché
in funzione
delle variabili (Q,W). Poiché 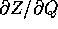 è
invertibile,
le (Q,W) costituiscono un buon sistema di coordinate, nel senso che
la trasformazione
è
invertibile,
le (Q,W) costituiscono un buon sistema di coordinate, nel senso che
la trasformazione
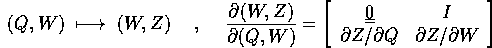
ha matrice jacobiana invertibile in 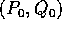 , e quindi per il
teorema della funzione inversa è un diffeomorfismo
almeno in un intorno di
, e quindi per il
teorema della funzione inversa è un diffeomorfismo
almeno in un intorno di 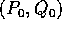 . Componendo poi questa
trasformazione con
. Componendo poi questa
trasformazione con 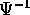 possiamo esprimere come funzione di
(Q,W) anche P=P(Q,W). Allora possiamo considerare la forma
differenziale
possiamo esprimere come funzione di
(Q,W) anche P=P(Q,W). Allora possiamo considerare la forma
differenziale 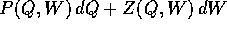 ; essa proviene, per
cambiamento di variabili, dalla forma differenziale
; essa proviene, per
cambiamento di variabili, dalla forma differenziale
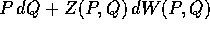 , ed applicando l'operatore di
differenziazione esterna si ottiene la
forma differenziale quadratica :
, ed applicando l'operatore di
differenziazione esterna si ottiene la
forma differenziale quadratica :
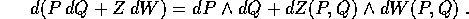
I coefficienti della forma 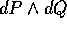 formano la matrice
antisimmetrica -J, opposta di quella che definisce la
struttura simplettica dello spazio delle fasi. La forma
formano la matrice
antisimmetrica -J, opposta di quella che definisce la
struttura simplettica dello spazio delle fasi. La forma
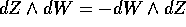 avrebbe, nel sistema di coordinate (W,Z),
coefficienti formanti la matrice J; per trovare la matrice dei
coefficienti di
avrebbe, nel sistema di coordinate (W,Z),
coefficienti formanti la matrice J; per trovare la matrice dei
coefficienti di 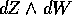 nelle coordinate (P,Q) si deve
applicare la regola di trasformazione per le forme differenziali
quadratiche, ottenendo
nelle coordinate (P,Q) si deve
applicare la regola di trasformazione per le forme differenziali
quadratiche, ottenendo 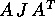 con
con 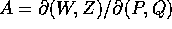 la matrice jacobiana del cambiamento di coordinate. Quindi la
matrice dei coefficienti della forma
la matrice jacobiana del cambiamento di coordinate. Quindi la
matrice dei coefficienti della forma 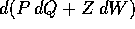 è
è
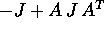 .
.
Per ipotesi la trasformazione da (P,Q) a (W,Z) è canonica, e per
il teorema delle trasformazioni canoniche

e quindi 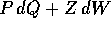 è una forma chiusa .
è una forma chiusa .
Poiché la proprietà di essere chiusa non dipende dal sistema di
coordinate (si veda Appendice B.2), anche
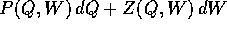 è chiusa, e per il teorema di
Poincaré è localmente una
forma esatta , in un intorno U di
è chiusa, e per il teorema di
Poincaré è localmente una
forma esatta , in un intorno U di
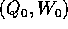 :
:
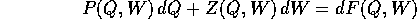
ossia, in termini di derivate parziali, il campo vettoriale
[P(Q,W), Z(Q,W)] è il campo gradiente di una funzione F(Q,W),
di classe 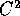 in un intorno di
in un intorno di 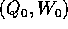 , dove
, dove 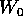 è
definito da
è
definito da 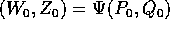 .
Valgono perciò le equazioni
.
Valgono perciò le equazioni
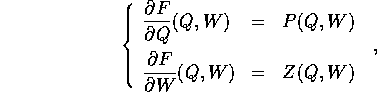
che definiscono implicitamente la trasformazione canonica 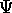 .
Inoltre, derivando la seconda delle due equazioni qua sopra
.
Inoltre, derivando la seconda delle due equazioni qua sopra
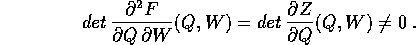
La trasformazione canonica 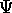 è univocamente definita
dalle equazioni implicite, poiché la condizione
è univocamente definita
dalle equazioni implicite, poiché la condizione
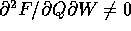 assicura che si può
ricavare dall'equazione che dà Z(Q,W), in un
intorno di
assicura che si può
ricavare dall'equazione che dà Z(Q,W), in un
intorno di 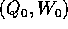 , la funzione implicita Q=Q(W,Z), che assieme a
P(Q(W,Z),W) definisce
, la funzione implicita Q=Q(W,Z), che assieme a
P(Q(W,Z),W) definisce 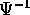 .
.
C.D.D.Esempio:
Esempio:
La funzione generatrice è una funzione di variabili
``miste'', cioè metà ``vecchie'' e metà ``nuove''. Però la
scelta di Q nella coppia di vettori (P,Q) e di W nella
coppia di vettori (W,Z) è arbitraria. Questo si può
eseguire componendo una trasformazione definita da F(Q,W)
con una trasformazione canonica che scambia ogni coordinata
con il suo momento coniugato, con un opportuno cambio di
segno, in uno dei due sistemi di coordinate (o in entrambi).
Con una funzione generatrice

si ottiene la trasformazione:
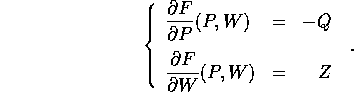
Con la funzione generatrice in variabili miste

si definisce la trasformazione
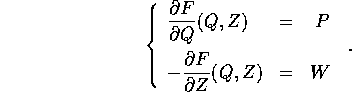
La quarta formula usa la funzione generatrice

e la fornisce la regola di trasformazione con due segni meno:
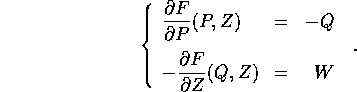
L'unica difficoltà nell'impiego di una qualunque di
queste quattro formule della trasformazione definita dalle
funzione generatrice è quella di ricordarsi la regola dei
segni. Per questo conviene, se possibile, attenersi al caso
F(Q,W) che ha tutti i segni positivi.
In effetti si potrebbero anche usare, come variabili
della funzione generatrice, alcuni vecchi momenti e
coordinate, ed i corrispondenti coniugati tra le nuove
variabili.
Il metodo della funzione generatrice per descrivere le
trasformazioni canoniche consente anche di descrivere
le soluzioni di un sistema hamiltoniano in termini di una sola
funzione generatrice. Supponiamo infatti di cercare
una trasformazione canonica che trasformi una hamiltoniana
data H(P,Q) in una banalmente integrabile, per esempio
K(W,Z)=K(W).
Se questo fosse possibile, renderebbe il sistema integrabile.
Infatti, le soluzioni nello spazio delle (W,Z) sarebbero
semplicemente, in funzione della condizione iniziale
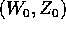 :
:
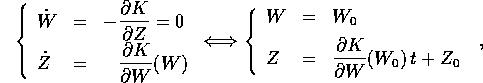
e sostituendo nella trasformazione inversa 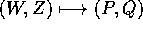 si avrebbero le soluzioni esplicite nello spazio delle
(P,Q). La funzione generatrice cercata S(Q,W) dovrebbe
definire una trasformazione canonica tale che
si avrebbero le soluzioni esplicite nello spazio delle
(P,Q). La funzione generatrice cercata S(Q,W) dovrebbe
definire una trasformazione canonica tale che
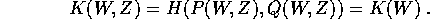
Per rendersi conto delle condizioni che questo impone alla
funzione generatrice S(Q,W) occorre esprimere la relazione
tra le due hamiltoniane in variabili miste (Q,W):
sostituendo
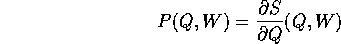
oltre che l'ovvia Q(Q,W)=Q, si trova un'equazione alle derivate
parziali (in generale nonlineare) detta
equazione di Hamilton-Jacobi nella funzione incognita S(Q,W):
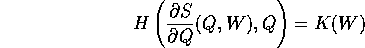
Si noti che la funzione K(W)
può essere qualsiasi. La funzione S deve essere tale
da funzionare correttamente da funzione generatrice di
una trasformazione canonica, almeno locale, quindi deve
soddisfare a

in tal caso si dice che S(Q,W) è una
funzione caratteristica di Hamilton-Jacobi per il
sistema hamiltoniano dato.
In generale, un'equazione differenziale a derivate
parziali è più difficile da risolvere di un'equazione
differenziale a derivate ordinarie. La
formulazione mediante equazione di Hamilton-Jacobi è
vantaggiosa quando si possono sfruttare alcune proprietà di
simmetria della funzione hamiltoniana che rendono l'equazione
a derivate parziali integrabile mediante quadrature .
Esempio:
-
- Consideriamo ancora l'oscillatore armonico :
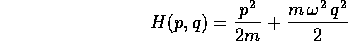
e scriviamone l'equazione di Hamilton-Jacobi:
la funzione generatrice incognita è della forma
S=S(q,w), e deve soddisfare a
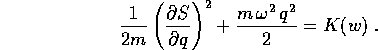
Poiché la sola derivata parziale della S che appare
nell'equazione è quella rispetto a q, possiamo ricondurci
ad una quadratura ricavando 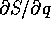 dall'equazione di Hamilton-Jacobi:
dall'equazione di Hamilton-Jacobi:
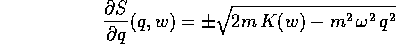
che si risolve localmente (cioè a meno della scelta del
segno davanti alla radice quadrata) con la quadratura:
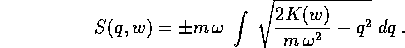
Benché questa quadratura sia esprimibile in termini finiti
con funzioni elementari, non è neppure necessario eseguirne
il calcolo, visto che nelle soluzioni appaiono solo le
derivate parziali di S. Per semplificare la derivata
rispetto a w, possiamo scegliere K(w)=w, ossia scegliere
come nuovo momento proprio l'energia; ne segue che 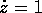 , cioè la nuova coordinata coincide con il tempo, a meno
di una costante:
, cioè la nuova coordinata coincide con il tempo, a meno
di una costante: 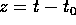 . Allora
. Allora
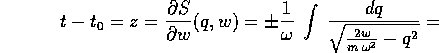
e questo è un integrale elementare che si esprime mediante
la funzione arcoseno:
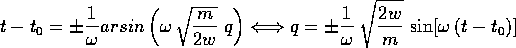
e sostituendo nella relazione che dà p in funzione
dell'energia w:
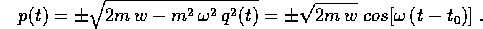
Al solito il segno va deciso sulla base di
considerazioni globali; per esempio i due segni + vanno
bene.
Il caso più notevole in cui l'equazione di Hamilton-Jacobi
può essere risolta esplicitamente (mediante quadrature)
è quello in cui è possibile la
separazione delle variabili , ossia si può trovare una
soluzione dell'equazione di Hamilton-Jacobi della forma
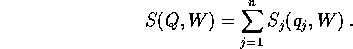
In tal caso l'equazione di Hamilton-Jacobi si riduce a tante equazioni
differenziali ordinarie, a variabili separabili, quanti sono i gradi
di libertà, ottenute separando le parti dell'equazione che dipendono
dalle singole 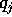 . La funzione S si trova allora per
quadrature. Questo sarà reso più chiaro da un esempio.
. La funzione S si trova allora per
quadrature. Questo sarà reso più chiaro da un esempio.
Esempio:
-
- Prendiamo il problema della forza centrale nel piano in
coordinate polari
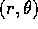 :
:
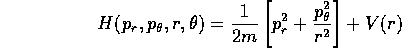
e cerchiamo una funzione generatrice
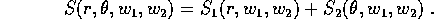
In questo caso la separazione delle variabili nell'equazione
di Hamilton-Jacobi è particolarmente semplice perché 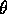 è
una variabile ciclica : nell'equazione
è
una variabile ciclica : nell'equazione
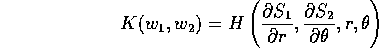
la variabile 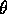 appare in realtà soltanto tramite
appare in realtà soltanto tramite
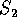 ; quindi possiamo supporre che
; quindi possiamo supporre che
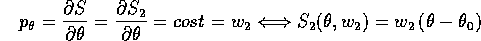
a meno di costanti
da cui si deduce che la costante di integrazione 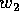 coincide con il valore costante del momento
coincide con il valore costante del momento 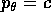 .
Sostituendo nell'equazione di Hamilton-Jacobi
.
Sostituendo nell'equazione di Hamilton-Jacobi
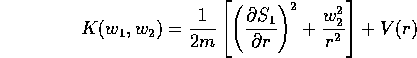
si può ridursi ad una quadratura ricavando l'espressione di
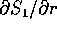 , cioè di
, cioè di 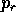 :
:
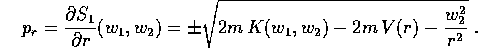
Poiché la soluzione contiene le derivate parziali di S
rispetto ai nuovi momenti 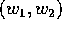 , conviene semplificare
l'espressione della soluzione scegliendo in modo opportuno
la funzione arbitraria
, conviene semplificare
l'espressione della soluzione scegliendo in modo opportuno
la funzione arbitraria 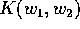 : per esempio si può
scegliere
: per esempio si può
scegliere 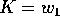 , cioè
, cioè 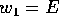 è l'energia, così come
abbiamo già visto che
è l'energia, così come
abbiamo già visto che 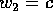 il momento angolare. Allora la
quadratura che dà S è:
il momento angolare. Allora la
quadratura che dà S è:
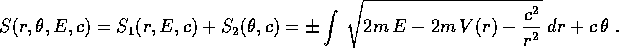
Nel nuovo sistema di coordinate 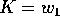 e quindi la variabile
coniugata
e quindi la variabile
coniugata 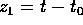 , mentre
, mentre
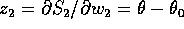 e le derivate parziali che forniscono la trasformazione e la
soluzione sono:
e le derivate parziali che forniscono la trasformazione e la
soluzione sono:
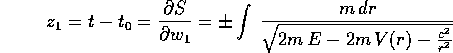
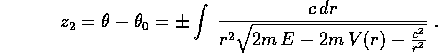
Il problema dei segni  va affrontato con un
argomento globale, per esempio osservando che si possono
scegliere gli estremi di integrazione nell'integrale
indefinito in modo che l'estremo inferiore sia
va affrontato con un
argomento globale, per esempio osservando che si possono
scegliere gli estremi di integrazione nell'integrale
indefinito in modo che l'estremo inferiore sia 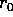 ; allora
le costanti di integrazione
; allora
le costanti di integrazione 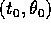 sono il tempo e,
rispettivamente, la direzione in cui la soluzione passa alla
distanza
sono il tempo e,
rispettivamente, la direzione in cui la soluzione passa alla
distanza 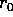 . Se la distanza r(t) ha un minimo, il che si
verifica con molti potenziali V(r), allora il momento
. Se la distanza r(t) ha un minimo, il che si
verifica con molti potenziali V(r), allora il momento
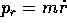 sarà negativo prima di arrivare ad
sarà negativo prima di arrivare ad 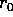 ,
positivo dopo, e con ragionamenti di questo tipo si possono
aggiustare correttamente i segni.
Si veda la Sezione 7.1.
,
positivo dopo, e con ragionamenti di questo tipo si possono
aggiustare correttamente i segni.
Si veda la Sezione 7.1.
Esempio:
-
- Prendiamo il problema della
forza centrale in tre dimensioni in
coordinate polari sferiche :
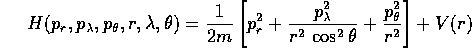
e cerchiamo la
funzione caratteristica di Hamilton-Jacobi
nella forma
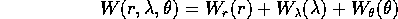
dove si è sottointesa la dipendenza dai nuovi momenti, che
saranno tre costanti di integrazione.
Sostituendo nell'equazione di Hamilton-Jacobi:
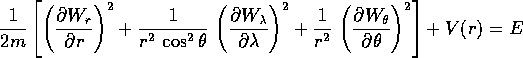
e dovendo il primo membro essere indipendente
dalla tre variabili 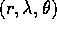 , si possono scrivere
tre separate equazioni contenenti le tre variabili.
La variabile
, si possono scrivere
tre separate equazioni contenenti le tre variabili.
La variabile 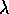 , essendo ciclica, appare solo in
, essendo ciclica, appare solo in
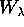 , e quindi
, e quindi

una costante che è facile identificare con la componente z
del momento angolare :
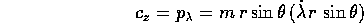
è la formula massa 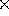 braccio
braccio 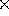 velocità.
Allora
velocità.
Allora 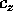 può essere scelto come uno dei nuovi momenti,
e
può essere scelto come uno dei nuovi momenti,
e 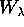 ha la semplice espressione
ha la semplice espressione

Sostituendo 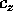 nell'equazione di Hamilton-Jacobi, si trova
nell'equazione di Hamilton-Jacobi, si trova
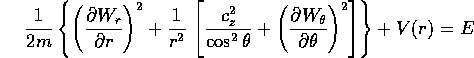
con la parentesi quadra che racchiude la parte dipendente da 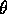 ;
perciò si può assumere che tale espressione sia una costante,
dipendente solo dai nuovi momenti.
Questa dipendenza è arbitraria,
ma si può scegliere facendo in modo che la nuova costante di
integrazione coincida con la lunghezza del vettore
momento angolare :
;
perciò si può assumere che tale espressione sia una costante,
dipendente solo dai nuovi momenti.
Questa dipendenza è arbitraria,
ma si può scegliere facendo in modo che la nuova costante di
integrazione coincida con la lunghezza del vettore
momento angolare :
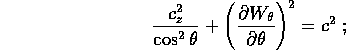
infatti sostituendo nella hamiltoniana:
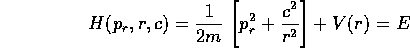
si ottiene la stessa funzione del caso piano, il che conferma che 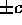 è la coordinata del vettore momento angolare perpendicolare al
piano del moto, quindi possiamo assumere (con opportuna scelta di
orientazione, cioè del verso in cui cresce
è la coordinata del vettore momento angolare perpendicolare al
piano del moto, quindi possiamo assumere (con opportuna scelta di
orientazione, cioè del verso in cui cresce 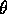 ) che c sia la
lunghezza del vettore momento angolare.
) che c sia la
lunghezza del vettore momento angolare.
L'equazione per 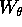 si ottiene risolvendo per
il momento
si ottiene risolvendo per
il momento 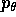 , cioè per la derivata di
, cioè per la derivata di
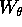 rispetto a
rispetto a 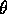 :
:
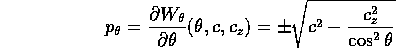
che si può risolvere per quadratura nella variabile
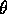 . A questo punto l'ultima delle tre funzioni
a variabili separate che compongono la funzione caratteristica
di Hamilton-Jacobi W si ottiene da:
. A questo punto l'ultima delle tre funzioni
a variabili separate che compongono la funzione caratteristica
di Hamilton-Jacobi W si ottiene da:
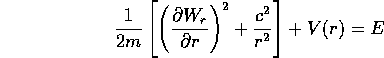
che coincide con l'equazione di Hamilton-Jacobi per un
problema ad un grado di libertà, e perciò è risolubile
per quadratura: basta ricavare 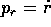 ed integrare
ed integrare
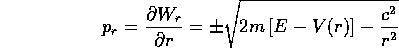
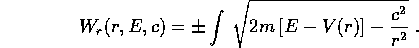
È disponibile ancora una scelta arbitraria, del terzo
dei nuovi momenti; oppure si può scegliere
l'espressione di E in funzione dei tre nuovi momenti.
Se si fa la scelta più semplice possibile, cioè si usa E
stessa come terzo momento, allora
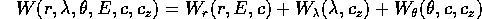
è la funzione caratteristica di Hamilton-Jacobi cercata.
La scelta dei segni  , ovvero la formula di soluzione
globale del problema, è chiarita dalla teoria
delle variabili azione-angolo ; si veda alla
Sezione 6.6.
, ovvero la formula di soluzione
globale del problema, è chiarita dalla teoria
delle variabili azione-angolo ; si veda alla
Sezione 6.6.




Next: 6.6 INTEGRABILITÀ
Up: 6 SISTEMI CONSERVATIVI: PIÙ
Previous: 6.4 SIMMETRIEINTEGRALI PRIMI
Andrea Milani
Thu Aug 14 11:30:04 MET DST 1997
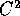 di
di 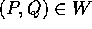 aperto di
aperto di
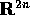 , mediante le equazioni di Hamilton
, mediante le equazioni di Hamilton
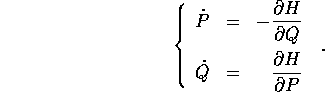
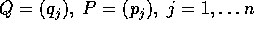 ; perciò si dice che il
sistema ha n gradi di libertà .
Per ogni coordinata
; perciò si dice che il
sistema ha n gradi di libertà .
Per ogni coordinata 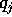 , la corrispondente
, la corrispondente 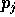 è il suo
momento coniugato .
L'insieme in cui possono variare
(P,Q) è lo spazio delle fasi .
è il suo
momento coniugato .
L'insieme in cui possono variare
(P,Q) è lo spazio delle fasi .
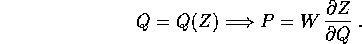
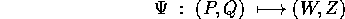
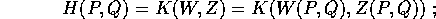
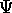 si dice una
trasformazione canonica
si dice una
trasformazione canonica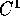 e con inversa
e con inversa 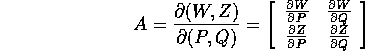

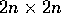

 matrici indentità
di tipo
matrici indentità
di tipo 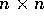 .
.
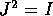 . Se si tiene a mente questa analogia,
sia l'enunciato che la dimostrazione di questo teorema sono
formalmente identici a quello del teorema delle
. Se si tiene a mente questa analogia,
sia l'enunciato che la dimostrazione di questo teorema sono
formalmente identici a quello del teorema delle
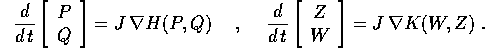
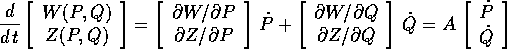
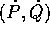 il secondo membro delle
equazioni di Hamilton nelle variabili (P,Q):
il secondo membro delle
equazioni di Hamilton nelle variabili (P,Q):
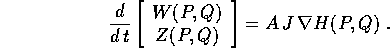
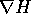 e quello
e quello 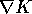 ; se facciamo l'ipotesi che le due
funzioni si corrispondano per valore, utilizzando il differenziale
della funzione composta:
; se facciamo l'ipotesi che le due
funzioni si corrispondano per valore, utilizzando il differenziale
della funzione composta:
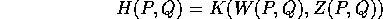
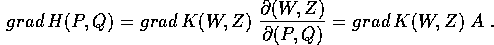
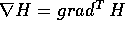
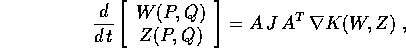
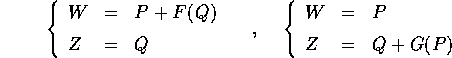
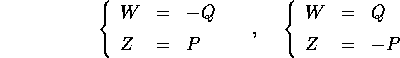
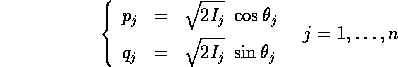
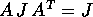 , allora valgono le seguenti
proprietà:
, allora valgono le seguenti
proprietà:

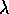 è un autovalore di A, anche
è un autovalore di A, anche 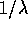 lo
è; sono gli stessi sia la
lo
è; sono gli stessi sia la 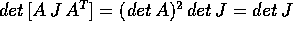 . Scriviamo il
. Scriviamo il
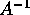 e proviamo che ha le stesse radici di
quello di A.
e proviamo che ha le stesse radici di
quello di A.
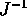 si deduce
si deduce 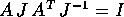 , quindi
, quindi 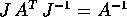 .
Allora il polinomio caratteristico per
.
Allora il polinomio caratteristico per 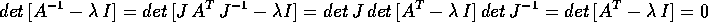
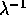 :
:
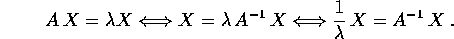
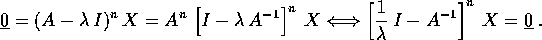
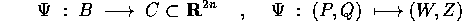
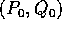 un punto di B tale che
un punto di B tale che 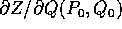 è una matrice invertibile.
Allora esiste un intorno U di
è una matrice invertibile.
Allora esiste un intorno U di 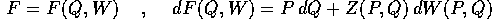
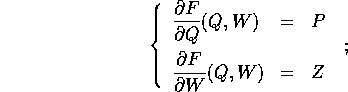
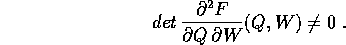
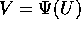 .
.
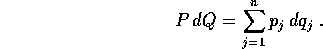
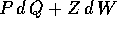 in funzione
delle variabili (Q,W). Poiché
in funzione
delle variabili (Q,W). Poiché 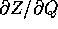 è
invertibile,
le (Q,W) costituiscono un buon sistema di coordinate, nel senso che
la trasformazione
è
invertibile,
le (Q,W) costituiscono un buon sistema di coordinate, nel senso che
la trasformazione
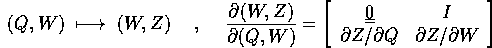
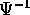 possiamo esprimere come funzione di
(Q,W) anche P=P(Q,W). Allora possiamo considerare la forma
differenziale
possiamo esprimere come funzione di
(Q,W) anche P=P(Q,W). Allora possiamo considerare la forma
differenziale 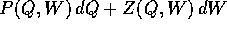 ; essa proviene, per
cambiamento di variabili, dalla forma differenziale
; essa proviene, per
cambiamento di variabili, dalla forma differenziale
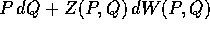 , ed applicando l'operatore di
, ed applicando l'operatore di
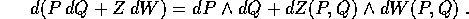
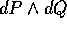 formano la matrice
antisimmetrica -J, opposta di quella che definisce la
formano la matrice
antisimmetrica -J, opposta di quella che definisce la
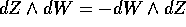 avrebbe, nel sistema di coordinate (W,Z),
coefficienti formanti la matrice J; per trovare la matrice dei
coefficienti di
avrebbe, nel sistema di coordinate (W,Z),
coefficienti formanti la matrice J; per trovare la matrice dei
coefficienti di 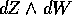 nelle coordinate (P,Q) si deve
applicare la regola di trasformazione per le forme differenziali
quadratiche, ottenendo
nelle coordinate (P,Q) si deve
applicare la regola di trasformazione per le forme differenziali
quadratiche, ottenendo 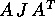 con
con 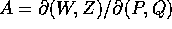 la matrice jacobiana del cambiamento di coordinate. Quindi la
matrice dei coefficienti della forma
la matrice jacobiana del cambiamento di coordinate. Quindi la
matrice dei coefficienti della forma 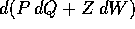 è
è
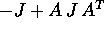 .
.

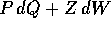 è una
è una 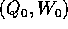 :
:
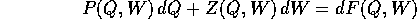
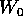 è
definito da
è
definito da 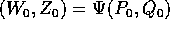 .
Valgono perciò le equazioni
.
Valgono perciò le equazioni
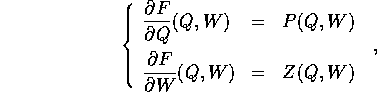
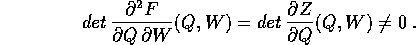
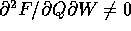 assicura che si può
ricavare dall'equazione che dà Z(Q,W), in un
intorno di
assicura che si può
ricavare dall'equazione che dà Z(Q,W), in un
intorno di 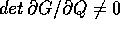 , allora si può definire una
trasformazione canonica che estende G allo spazio delle
fasi, usando la funzione generatrice:
, allora si può definire una
trasformazione canonica che estende G allo spazio delle
fasi, usando la funzione generatrice:
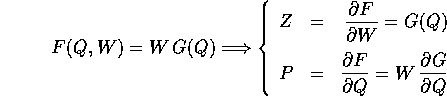

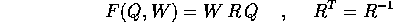

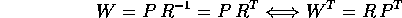

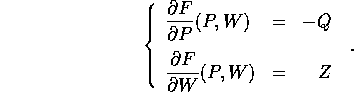

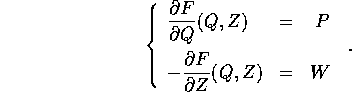

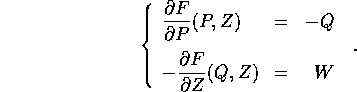
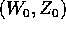 :
:
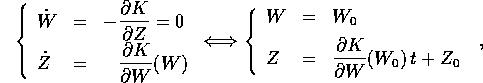
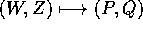 si avrebbero le soluzioni esplicite nello spazio delle
(P,Q). La
si avrebbero le soluzioni esplicite nello spazio delle
(P,Q). La 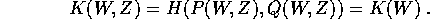
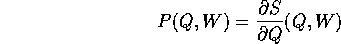
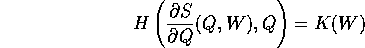

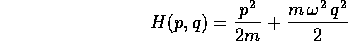
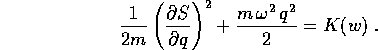
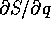 dall'equazione di Hamilton-Jacobi:
dall'equazione di Hamilton-Jacobi:
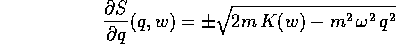
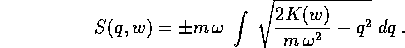
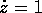 , cioè la nuova coordinata coincide con il tempo, a meno
di una costante:
, cioè la nuova coordinata coincide con il tempo, a meno
di una costante: 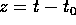 . Allora
. Allora
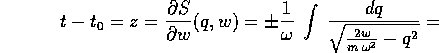
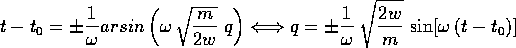
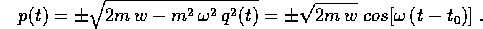
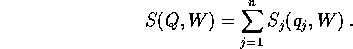
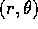 :
:
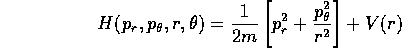
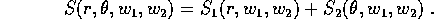
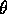 è
una
è
una 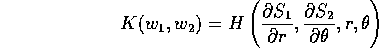
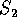 ; quindi possiamo supporre che
; quindi possiamo supporre che
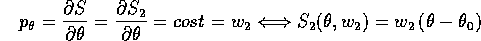
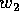 coincide con il valore costante del momento
coincide con il valore costante del momento 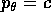 .
Sostituendo nell'equazione di Hamilton-Jacobi
.
Sostituendo nell'equazione di Hamilton-Jacobi
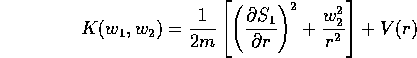
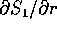 , cioè di
, cioè di 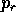 :
:
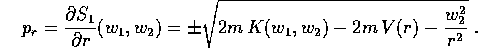
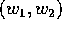 , conviene semplificare
l'espressione della soluzione scegliendo in modo opportuno
la funzione arbitraria
, conviene semplificare
l'espressione della soluzione scegliendo in modo opportuno
la funzione arbitraria 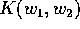 : per esempio si può
scegliere
: per esempio si può
scegliere 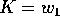 , cioè
, cioè 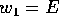 è l'energia, così come
abbiamo già visto che
è l'energia, così come
abbiamo già visto che 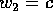 il momento angolare. Allora la
quadratura che dà S è:
il momento angolare. Allora la
quadratura che dà S è:
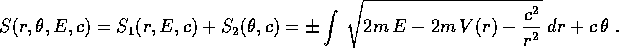
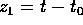 , mentre
, mentre
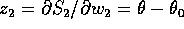 e le derivate parziali che forniscono la trasformazione e la
soluzione sono:
e le derivate parziali che forniscono la trasformazione e la
soluzione sono:
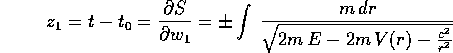
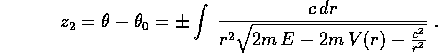
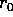 ; allora
le costanti di integrazione
; allora
le costanti di integrazione 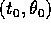 sono il tempo e,
rispettivamente, la direzione in cui la soluzione passa alla
distanza
sono il tempo e,
rispettivamente, la direzione in cui la soluzione passa alla
distanza 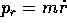 sarà negativo prima di arrivare ad
sarà negativo prima di arrivare ad 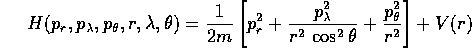
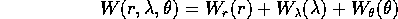
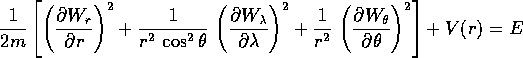
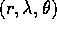 , si possono scrivere
tre separate equazioni contenenti le tre variabili.
La variabile
, si possono scrivere
tre separate equazioni contenenti le tre variabili.
La variabile 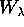 , e quindi
, e quindi

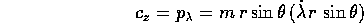
 braccio
braccio 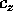 può essere scelto come uno dei nuovi momenti,
e
può essere scelto come uno dei nuovi momenti,
e 
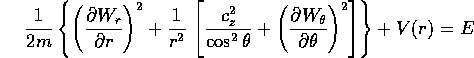
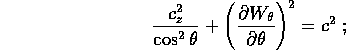
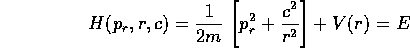
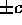 è la coordinata del vettore momento angolare perpendicolare al
piano del moto, quindi possiamo assumere (con opportuna scelta di
orientazione, cioè del verso in cui cresce
è la coordinata del vettore momento angolare perpendicolare al
piano del moto, quindi possiamo assumere (con opportuna scelta di
orientazione, cioè del verso in cui cresce 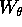 si ottiene risolvendo per
il momento
si ottiene risolvendo per
il momento 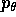 , cioè per la derivata di
, cioè per la derivata di
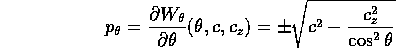
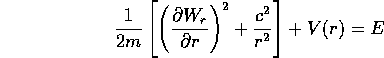
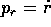 ed integrare
ed integrare