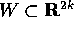 da una lagrangiana
da una lagrangiana 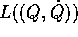 è
interessante uno speciale cambiamento di coordinate, ottenuto
sostituendo alla
velocità generalizzata
è
interessante uno speciale cambiamento di coordinate, ottenuto
sostituendo alla
velocità generalizzata 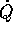 il
vettore dei momenti coniugati ,
che formano il vettore riga
il
vettore dei momenti coniugati ,
che formano il vettore riga
Sommario Un sistema lagrangiano può essere trasformato in un sistema hamiltoniano, purché sia soddisfatta una condizione di non degenerazione. Questo consente per esempio di mettere in evidenza l'integrale dell'energia in un sistema lagrangiano derivato da un sistema newtoniano. La trasformazione di Legendre consente anche di mettere in evidenza le simmetrie del sistema mediante variabili cicliche. Sistemi lagrangiani - o hamiltoniani - con un numero sufficiente di variabili cicliche possono essere ridotti ad un grado di libertà, quindi sono integrabili, come nel caso della forza centrale.
Come nel caso ad un grado di libertà, per un sistema descritto in un o
spazio delle fasi 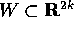 da una lagrangiana
da una lagrangiana 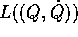 è
interessante uno speciale cambiamento di coordinate, ottenuto
sostituendo alla
velocità generalizzata
è
interessante uno speciale cambiamento di coordinate, ottenuto
sostituendo alla
velocità generalizzata 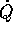 il
vettore dei momenti coniugati ,
che formano il vettore riga
il
vettore dei momenti coniugati ,
che formano il vettore riga

Supponiamo che questa relazione sia definita ed invertibile
tra l'aperto W delle 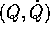 ed un
aperto
ed un
aperto 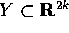 delle (P,Q), cioè che sia definita
delle (P,Q), cioè che sia definita 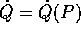 : allora possiamo
definire la trasformata di Legendre
: allora possiamo
definire la trasformata di Legendre
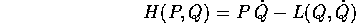
che fornisce una funzione di Hamilton H(P,Q), definita e di
classe 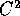 su Y, quando sia nota la funzione di Lagrange
su Y, quando sia nota la funzione di Lagrange
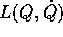 , definita e di classe
, definita e di classe 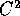 su Z. viceversa, data H si
ottiene L trasformandola in modo identico e con identiche condizioni
di invertibilità:
su Z. viceversa, data H si
ottiene L trasformandola in modo identico e con identiche condizioni
di invertibilità:
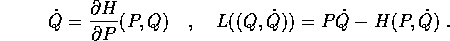
La condizione perché la trasformazione di Legendre inversa
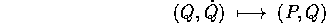
sia almeno localmente invertibile (con inversa differenziabile) è che la sua matrice jacobiana sia invertibile: deve valere la condizione di non degenerazione
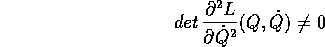
in ogni punto di Z.
A differenza del caso con un solo grado di libertà, la condizione di non degenerazione non è sufficiente ad assicurare l'invertibilità globale della trasformazione di Legendre, perché il teorema della funzione inversa in più variabili è soltanto locale. L'invertibilità globale va quindi verificata caso per caso, oppure bisogna limitarsi a conclusioni valide solo su di un intorno delle condizioni iniziali nello spazio delle fasi.
Teorema della trasformata di Legendre :
Sia data una lagrangiana 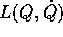 di classe
di classe 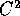 e non
degenere sull'aperto
e non
degenere sull'aperto 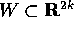 , tale che
la trasformazione
, tale che
la trasformazione 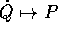 definita da
definita da

sia invertibile (per ogni Q) (perciò tale che la trasformazione
inversa di Legendre definisca un
diffeomorfismo di classe 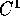 tra W e
tra W e 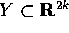 ).
).
Allora la funzione di Hamilton H(P,Q), di classe 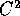 su Y, definita dalla trasformata di Legendre,
è tale che
le equazioni di Hamilton
su Y, definita dalla trasformata di Legendre,
è tale che
le equazioni di Hamilton
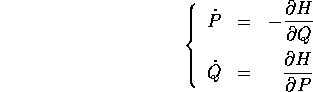
e le equazioni di Lagrange
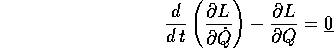
hanno soluzioni che si corrispondono per la trasformazione di Legendre inversa.
Viceversa, sia data una funzione di Hamilton H(P,Q), di classe
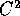 e non degenere sull'aperto
e non degenere sull'aperto 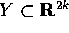 , cioè tale che
, cioè tale che
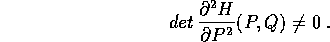
Se la trasformazione di Legendre 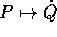 definita dalla seconda delle equazioni di Hamilton
definita dalla seconda delle equazioni di Hamilton

è invertibile (per ogni Q) (quindi se definisce un diffeomorfismo
di classe 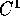 tra Y e
tra Y e 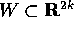 ), allora la funzione di
Lagrange, di classe
), allora la funzione di
Lagrange, di classe 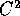 su W, definita dalla trasformata di
Legendre, è tale che le corrispondenti equazioni di Lagrange hanno
soluzioni che corrispondono, per la trasformazione di Legendre, a
quelle delle equazioni di Hamilton.
su W, definita dalla trasformata di
Legendre, è tale che le corrispondenti equazioni di Lagrange hanno
soluzioni che corrispondono, per la trasformazione di Legendre, a
quelle delle equazioni di Hamilton.
Dimostrazione:
Per esempio, se la lagrangiana è definita da
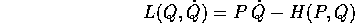
dove la trasformazione di Legendre fornisce la relazione
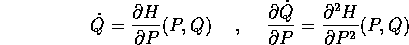
allora l'ipotesi di non degenerazione di H(P,Q) consente di
applicare il teorema delle funzioni implicite ,
ricavando localmente 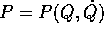 e sostituendo
e sostituendo
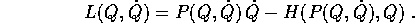
Ora calcoliamo, usando questa equazione, le derivate parziali
di 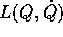 :
:
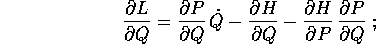
utilizzando l'equazione di Hamilton 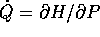 l'espressione si semplifica in
l'espressione si semplifica in

Il procedimento è identico per
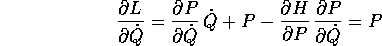
che è la trasformazione di Legendre inversa; a questo punto il primo membro dell'equazione di Lagrange
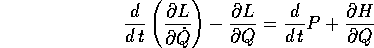
si annulla come conseguenza dell'equazione di Hamilton per
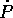 .
.
Viceversa, se la lagrangiana è nota ed è non degenere, allora
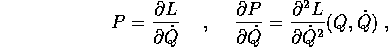
quindi si può applicare il teorema delle funzioni implicite
per ricavare localmente 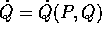 e sostituire
nella trasformata di Legendre che definisce H(P,Q):
e sostituire
nella trasformata di Legendre che definisce H(P,Q):
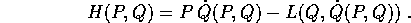
Derivando,
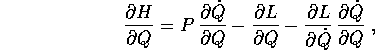
che si semplifica usando la definizione di P data dalla trasformazione di Legendre inversa

le altre derivate parziali si semplificano analogamente in
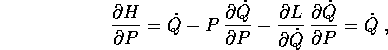
fornendo una delle due equazioni di Hamilton. L'altra segue dalle equazioni di Lagrange:
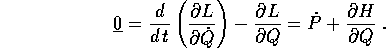
Le condizioni di non degenerazione sulla hamiltoniana
H(P,Q) e sulla lagrangiana 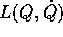 , che si corrispondono per
la trasformata di Legendre, assicurano entrambe che la
trasformata di Legendre è localmente invertibile; sono
quindi equivalenti.
, che si corrispondono per
la trasformata di Legendre, assicurano entrambe che la
trasformata di Legendre è localmente invertibile; sono
quindi equivalenti.
I due sistemi lagrangiano e hamiltoniano, che si ottengono l'uno dall'altro usando la trasformata di Legendre nel caso non degenere, esprimono dinamiche equivalenti , ma il sistema hamiltoniano ha il vantaggio di avere automaticamente un integrale primo:
Proprietà:
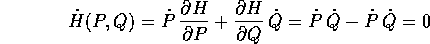
Una lagrangiana degenere è perfettamente adatta a definire un sistema dinamico, che però potrebbe non avere un integrale dell'energia. Una hamiltoniana degenere definisce un sistema hamiltoniano che non può essere convertito in uno lagrangiano, ma che ha ugualmente un integrale primo H(P,Q)=cost; non bisogna però presumere che l'integrale definito dalla hamiltoniana possa sempre essere interpretato come energia. Invece non sono necessarie né la condizione di convessità, né altre condizioni sui segni degli autovalori delle matrici delle derivate seconde. Questo perché, a differenza di quanto accade con un solo grado di libertà, gli autovalori possono cambiare di segno senza che la matrice diventi degenere.
Se la funzione di Lagrange è quella dei sistemi newtoniani
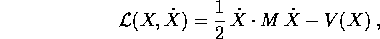
allora la trasformazione di Legendre è una relazione
lineare tra velocità 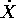 e momenti Y:
e momenti Y:
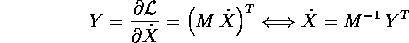
che è sempre invertibile, poiché M è definita positiva; si noti che Y è un vettore riga. La trasformata di Legendre fornisce una hamiltoniana che è ancora quadratica nelle Y:
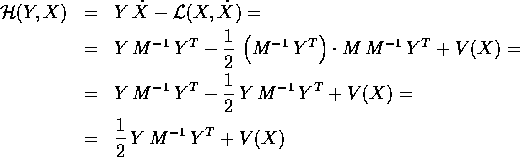
La formula qui sopra si semplifica perché il prodotto
scalare 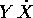 coincide con 2T.
coincide con 2T.
Il risultato si estende al caso generico di una lagrangiana
che deriva da un sistema newtoniano per effetto di un
cambiamento di coordinate; ciò che conta è che 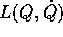 sia una forma quadratica nelle
sia una forma quadratica nelle 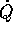 priva di termini
lineari:
priva di termini
lineari:
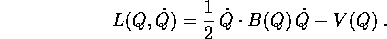
La trasformazione di Legendre inversa è lineare (nelle 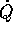 ), invertibile se supponiamo B(Q) definita positiva per
ogni Q:
), invertibile se supponiamo B(Q) definita positiva per
ogni Q:
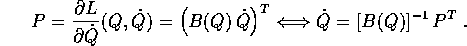
Grazie alla relazione
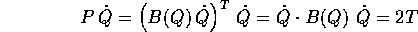
si semplifica la funzione di Hamilton, che coincide con l'energia totale
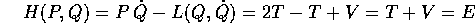
ed è ancora una forma quadratica nelle P, senza termini lineari, la cui matrice è l'inversa della matrice che appare nella lagrangiana:
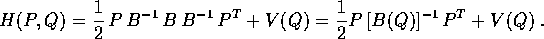
In questo caso l'integrale primo definito dalla hamiltoniana e l'integrale dell'energia ottenuto dal sistema newtoniano coincidono, nel senso che sono la stessa funzione nei due diversi sistemi di coordinate.
I cambiamenti di coordinate nelle equazioni di Lagrange vengono utilizzati per vari scopi: per esempio, rendere più semplice la forma delle equazioni e delle soluzioni. Una semplificazione notevole si ottiene quando esiste una variabile ciclica , cioè una coordinata che non compare nella funzione di Lagrange: se per esempio supponiamo che sia la prima coordinata, cioè che
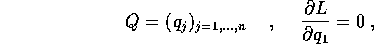
allora la prima delle equazioni di Lagrange avrà la forma più semplice
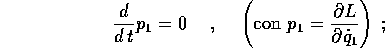
allora il momento coniugato alla variabile ciclica (quello con lo stesso indice) risulterà un integrale primo.
La definizione di variabile ciclica si applica anche ad una funzione di Hamilton: se

allora una delle corrispondenti equazioni di Hamilton è

Si può verificare, derivando rispetto a 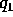 la
trasformazione di Legendre, che la variabile
la
trasformazione di Legendre, che la variabile 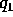 è ciclica
per la
è ciclica
per la 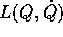 se e solo se lo è per la H(P,Q), dove si
intende che le due funzioni siano legate dalla trasformata di Legendre.
se e solo se lo è per la H(P,Q), dove si
intende che le due funzioni siano legate dalla trasformata di Legendre.
Per sfruttare pienamente il vantaggio della presenza di una variabile ciclica, bisogna separare completamente la dinamica della variabile ciclica da quella delle altre variabili: il modo più semplice è quello di utilizzare le equazioni di Hamilton per la variabile ciclica ed il suo momento coniugato:
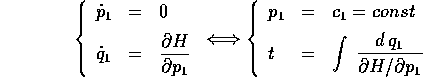
dove la seconda è risolta ricavando l'inversa della legge
oraria per quadratura ; si noti che nella funzione integranda
compaiono le coordinate 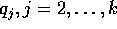 ed i momenti
ed i momenti
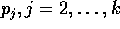 come funzioni del tempo, e la costante
come funzioni del tempo, e la costante
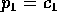 . Le soluzioni per le
. Le soluzioni per le 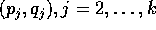 dovranno essere ottenute dalle altre equazioni (di Lagrange
o di Hamilton) a k-1 gradi di libertà, con il parametro
dovranno essere ottenute dalle altre equazioni (di Lagrange
o di Hamilton) a k-1 gradi di libertà, con il parametro
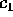 .
.
Le coordinate polari possono essere impiegate efficacemente per semplificare le equazioni di Lagrange, in particolare se semplificano l'energia potenziale.
Prendiamo 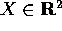 , ed eseguiamo il cambiamento di
coordinate che passa alle coordinate polari Q:
, ed eseguiamo il cambiamento di
coordinate che passa alle coordinate polari Q:
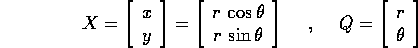
con matrice jacobiana
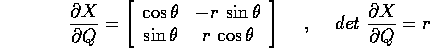
che è non singolare per r>0, e che descrive la trasformazione controvariante delle velocità generalizzate:
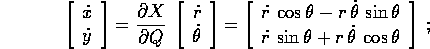
allora l'energia cinetica del corpo puntiforme di massa m
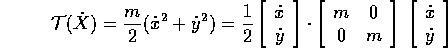
si trasforma in coordinate polari in
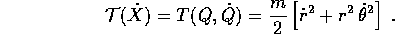
Questo cambiamento di coordinate si dimostra particolarmente utile quando il campo di forze è del tipo della forza centrale , ossia orientato radialmente verso l'origine, con intensità che dipende solo del raggio
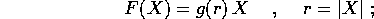
supponiamo che g(r) sia una funzione 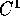 almeno per r>0. I campi di
forza centrale sono sempre conservativi:
almeno per r>0. I campi di
forza centrale sono sempre conservativi:
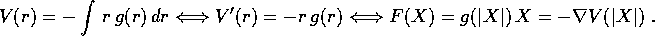
Quindi il sistema newtoniano con forza centrale si può sempre descrivere in forma lagrangiana con
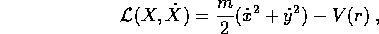
che in coordinate polari diventa
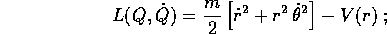
ma allora 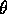 è una variabile ciclica , e le equazioni di Lagrange
risultano particolarmente semplici. L'equazione di
Lagrange relativa a
è una variabile ciclica , e le equazioni di Lagrange
risultano particolarmente semplici. L'equazione di
Lagrange relativa a 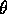 si riduce a
si riduce a
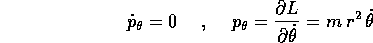
la cui soluzione è 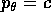 con c costante (da
determinare in base alle condizioni iniziali), mentre quella
per la coordinata r contiene il momento coniugato
con c costante (da
determinare in base alle condizioni iniziali), mentre quella
per la coordinata r contiene il momento coniugato

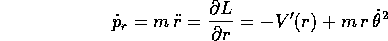
e si semplifica sostituendo la trasformazione di Legendre,
cioè l'espressione di 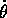 in funzione della costante c:
in funzione della costante c:
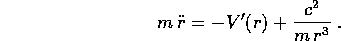
In conclusione il problema del corpo puntiforme nel piano con forza centrale si riduce ad un sistema ad un grado di libertà, che si può anche considerare come un sistema newtoniano, pur di considerare un'energia potenziale effettiva K(r) che contiene un termine supplementare rispetto all'energia potenziale del campo di forze:
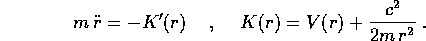
La trasformata di Legendre fornisce la hamiltoniana
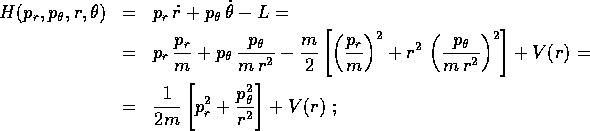
Le equazioni di Hamilton per la variabile ciclica 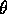 sono
sono
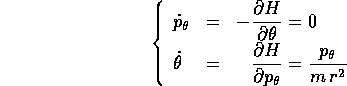
e per la variabile r
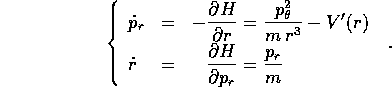
Se si sostituisce al momento 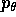 il suo valore costante
c, anche il sistema hamiltoniano appare come un sistema ad
un grado di libertà con parametro c:
il suo valore costante
c, anche il sistema hamiltoniano appare come un sistema ad
un grado di libertà con parametro c:
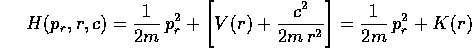
in cui compare l'energia potenziale effettiva K(r) al posto dell'energia potenziale V(r). Lo studio qualitativo di questo sistema dinamico risulterà semplicemente dallo studio dalle proprietà della funzione K(r), con i metodi visti nella Sezione 5.2.
Il termine supplementare 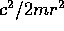 può essere
interpretato come energia potenziale associato alla
forza apparente centrifuga ; in questo caso la riduzione
all'unico grado di libertà r consiste nel rendere il riferimento
dell'osservatore solidale con il punto materiale.
può essere
interpretato come energia potenziale associato alla
forza apparente centrifuga ; in questo caso la riduzione
all'unico grado di libertà r consiste nel rendere il riferimento
dell'osservatore solidale con il punto materiale.
Consideriamo le coordinate polari sferiche nello spazio
 :
:
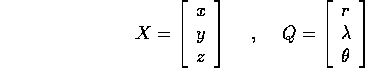
con la trasformazione X=X(Q) definita da:
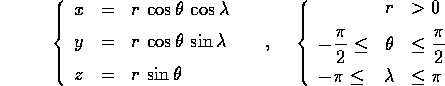
dove r=|(x,y,z)| è la distanza dall'origine, 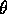 è
la latitudine e
è
la latitudine e 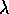 la longitudine (rispetto ad un piano
equatoriale e ad un asse polare arbitrari).
la longitudine (rispetto ad un piano
equatoriale e ad un asse polare arbitrari).
Le derivate parziali della trasformazione formano una matrice
jacobiana 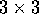
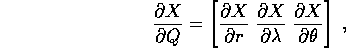
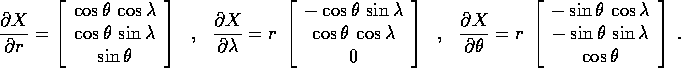
Supponiamo di avere ancora un corpo puntiforme di massa m ed un campo di forza centrale con energia potenziale V(r): come nel caso bidimensionale,
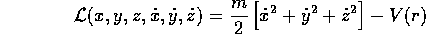
è la lagrangiana in coordinate cartesiane, mentre in funzione delle coordinate polari è
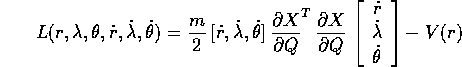
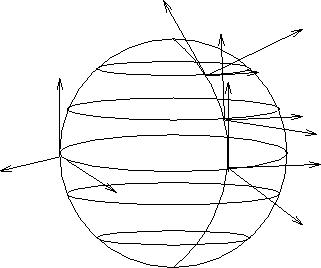
Figure 6.1: Nelle coordinate polari sferiche, i tre vettori
delle derivate parziali rispetto alle tre coordinate sono sempre tra
loro ortogonali.
Questa espressione si semplifica notevolmente perché i tre vettori colonna della matrice jacobiana sono tra loro ortogonali:
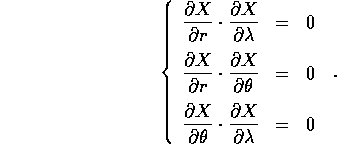
Quindi la matrice della forma quadratica, che esprime l'energia cinetica in coordinate polari, resta diagonale:
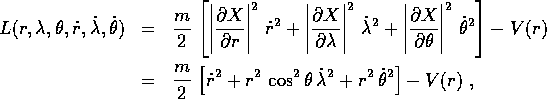
ed anche in questo caso c'è una variabile ciclica, cioè
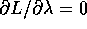 .
.
La trasformata di Legendre si può calcolare con la formula
della matrice inversa: se la matrice che esprime 2T
in funzione di 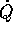 è
è
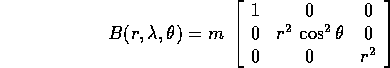
(si noti che dipende effettivamente da 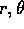 ma non da
ma non da
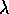 ), allora la matrice che esprime 2T in funzione di
P è
), allora la matrice che esprime 2T in funzione di
P è
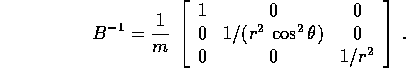
Quindi la hamiltoniana è
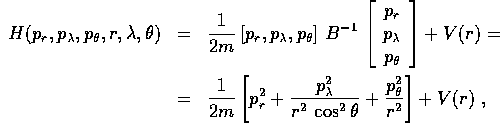
che, utilizzando l'integrale primo che deriva
dalla variabile ciclica 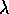 ,
può essere interpretata come una hamiltoniana a due
gradi di libertà: posto
,
può essere interpretata come una hamiltoniana a due
gradi di libertà: posto 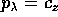 ,
si ha
,
si ha
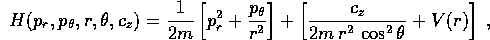
con solo quattro variabili dinamiche ed un parametro
(dipendente dalle condizioni iniziali, ma indipendente dal
tempo) 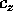 .
.
Anche nel caso tridimensionale il problema con forza centrale è integrabile, ma questo richiede l'eliminazione di una seconda variabile che non è ciclica; il metodo da impiegare sarà spiegato nella Sezione 6.5.