



Next: B.2 CALCOLO IN PIÙ
Up: B REQUISITI DI ALGEBRA
Previous: B REQUISITI DI ALGEBRA
Data una matrice quadrata A di tipo 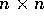 , i vettori
, i vettori
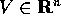 tali che
tali che 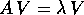 sono gli autovettori di A; i numeri
sono gli autovettori di A; i numeri 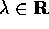 sono gli autovalori . Poiché la stessa matrice
definisce anche una trasformazione lineare di
sono gli autovalori . Poiché la stessa matrice
definisce anche una trasformazione lineare di 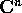 in sé,
A può anche avere autovalori ed autovettori complessi.
Gli autovalori sono le radici del
polinomio caratteristico
in sé,
A può anche avere autovalori ed autovettori complessi.
Gli autovalori sono le radici del
polinomio caratteristico 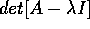 , che ha grado
n, ed i cui coefficienti sono invarianti della matrice
A, come la traccia ed il determinante.
, che ha grado
n, ed i cui coefficienti sono invarianti della matrice
A, come la traccia ed il determinante.
La molteplicità dell'autovalore 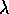 è la dimensione del
sottospazio vettoriale (di
è la dimensione del
sottospazio vettoriale (di 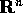 , oppure di
, oppure di 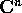 ) degli
autovettori con quell'autovalore.
La molteplicità algebrica
del numero
) degli
autovettori con quell'autovalore.
La molteplicità algebrica
del numero 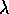 come radice del polinomio caratteristico
è maggiore o uguale della molteplicità dell'autovalore.
come radice del polinomio caratteristico
è maggiore o uguale della molteplicità dell'autovalore.
Teorema fondamentale dell'algebra : Il numero di
radici di un'equazione algebrica in una variabile, con
polinomio di grado n, contando ogni radice con la sua
molteplicità algebrica, è n.
Teorema di Hamilton-Cayley :
Se 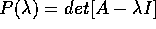 è il polinomio
caratteristico della matrice A, allora P(A) è la matrice nulla.
è il polinomio
caratteristico della matrice A, allora P(A) è la matrice nulla.
Teorema della decomposizione S + N :
Ogni matrice A di tipo 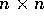 si può scrivere in uno ed un
solo modo come somma di una matrice semisemplice e di una
matrice nilpotente : A= S + N che commutano tra
loro: SN=NS.
si può scrivere in uno ed un
solo modo come somma di una matrice semisemplice e di una
matrice nilpotente : A= S + N che commutano tra
loro: SN=NS.
Si noti che questo teorema vale sia per A a coefficienti
complessi (con S,N pure a coefficienti in 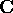 ), sia per A a
coefficienti reali, nel qual caso anche S,N sono a coefficienti
reali.
), sia per A a
coefficienti reali, nel qual caso anche S,N sono a coefficienti
reali.
Teorema della forma canonica dei nilpotenti :
Per ogni matrice quadrata N che sia nilpotente , cioè tale
che 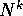 è la matrice nulla (per qualche intero k), esiste una
matrice invertibile B tale che
è la matrice nulla (per qualche intero k), esiste una
matrice invertibile B tale che 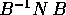 ha tutti i coefficienti
nulli salvo quelli immediatamente sotto la diagonale principale, che
valgono o 0 o 1.
ha tutti i coefficienti
nulli salvo quelli immediatamente sotto la diagonale principale, che
valgono o 0 o 1.
Teorema di Jordan :
Per ogni matrice quadrata A a coefficienti complessi, esiste una
matrice invertibile B (pure a coefficienti complessi) tale che
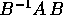 è nella forma canonica di Jordan , cioè una
matrice a blocchi
è nella forma canonica di Jordan , cioè una
matrice a blocchi 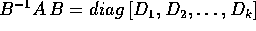 , con
ogni
, con
ogni 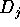 un blocco di Jordan della forma
un blocco di Jordan della forma 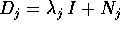 , dove
, dove 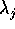 è un autovalore di A (reale o complesso) ed
è un autovalore di A (reale o complesso) ed 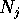 è un nilpotente in forma canonica con tutti i coefficienti
immediatamente sotto la diagonale principale uguali ad 1, e gli altri
nulli.
è un nilpotente in forma canonica con tutti i coefficienti
immediatamente sotto la diagonale principale uguali ad 1, e gli altri
nulli.
Per ogni matrice A a coefficienti reali, esiste una
matrice invertibile B (pure a coefficienti reali) tale che
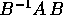 è nella forma canonica di Jordan reale
è nella forma canonica di Jordan reale
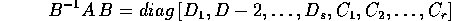
dove ciascun blocco di Jordan reale è della forma
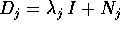 , dove
, dove 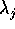 è un autovalore reale di
A, oppure
è un autovalore reale di
A, oppure
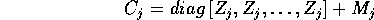
dove 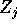 è la matrice
è la matrice 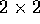 che rappresenta il numero
complesso
che rappresenta il numero
complesso 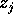 , con
, con 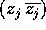 una coppia di autovalori
complessi coniugati di A, ed
una coppia di autovalori
complessi coniugati di A, ed 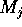 è un nilpotente con tutti i
coefficienti due diagonali sotto la diagonale principale uguali ad 1, e
gli altri nulli.
è un nilpotente con tutti i
coefficienti due diagonali sotto la diagonale principale uguali ad 1, e
gli altri nulli.
Teorema di diagonalizzazione delle forme quadratiche :
Ogni matrice quadrata e simmetrica 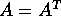 ammette una matrice
R ortogonale (con
ammette una matrice
R ortogonale (con 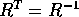 ) tale che
) tale che 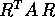 è una
matrice diagonale, con sulla diagonale gli autovalori, tutti
reali, di A.
è una
matrice diagonale, con sulla diagonale gli autovalori, tutti
reali, di A.
Teorema di diagonalizzazione simultanea :
Ogni coppia di matrici quadrate e simmetriche 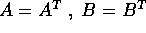 , tale
che almeno una delle due sia definita positiva, ammette una matrice
R invertibile che le diagonalizza simultaneamente, ossia tale che
sia
, tale
che almeno una delle due sia definita positiva, ammette una matrice
R invertibile che le diagonalizza simultaneamente, ossia tale che
sia 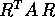 che
che 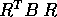 sono matrici diagonali.
sono matrici diagonali.
Bibliografia :
- Abeasis, S. : Algebra lineare e geometria, Zanichelli,
Bologna 1990.
- Lang, S. : Algebra lineare, Boringhieri, Torino 1970.




Next: B.2 CALCOLO IN PIÙ
Up: B REQUISITI DI ALGEBRA
Previous: B REQUISITI DI ALGEBRA
Andrea Milani
Thu Aug 14 11:30:04 MET DST 1997
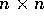 , i vettori
, i vettori
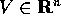 tali che
tali che 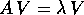 sono gli autovettori di A; i numeri
sono gli autovettori di A; i numeri 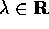 sono gli autovalori . Poiché la stessa matrice
definisce anche una trasformazione lineare di
sono gli autovalori . Poiché la stessa matrice
definisce anche una trasformazione lineare di 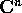 in sé,
A può anche avere autovalori ed autovettori complessi.
Gli autovalori sono le radici del
polinomio caratteristico
in sé,
A può anche avere autovalori ed autovettori complessi.
Gli autovalori sono le radici del
polinomio caratteristico 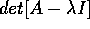 , che ha grado
n, ed i cui coefficienti sono invarianti della matrice
A, come la traccia ed il determinante.
, che ha grado
n, ed i cui coefficienti sono invarianti della matrice
A, come la traccia ed il determinante.
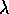 è la dimensione del
sottospazio vettoriale (di
è la dimensione del
sottospazio vettoriale (di 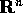 , oppure di
, oppure di 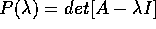 è il polinomio
caratteristico della matrice A, allora P(A) è la matrice nulla.
è il polinomio
caratteristico della matrice A, allora P(A) è la matrice nulla.
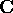 ), sia per A a
coefficienti reali, nel qual caso anche S,N sono a coefficienti
reali.
), sia per A a
coefficienti reali, nel qual caso anche S,N sono a coefficienti
reali.
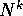 è la matrice nulla (per qualche intero k), esiste una
matrice invertibile B tale che
è la matrice nulla (per qualche intero k), esiste una
matrice invertibile B tale che 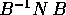 ha tutti i coefficienti
nulli salvo quelli immediatamente sotto la diagonale principale, che
valgono o 0 o 1.
ha tutti i coefficienti
nulli salvo quelli immediatamente sotto la diagonale principale, che
valgono o 0 o 1.
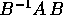 è nella forma canonica di Jordan
è nella forma canonica di Jordan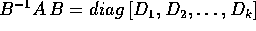 , con
ogni
, con
ogni 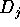 un blocco di Jordan
un blocco di Jordan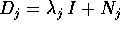 , dove
, dove 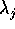 è un autovalore di A (reale o complesso) ed
è un autovalore di A (reale o complesso) ed 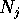 è un nilpotente in forma canonica con tutti i coefficienti
immediatamente sotto la diagonale principale uguali ad 1, e gli altri
nulli.
è un nilpotente in forma canonica con tutti i coefficienti
immediatamente sotto la diagonale principale uguali ad 1, e gli altri
nulli.
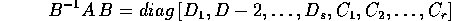
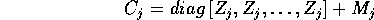
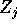 è la matrice
è la matrice 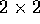 che rappresenta il numero
complesso
che rappresenta il numero
complesso 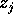 , con
, con 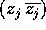 una coppia di autovalori
complessi coniugati di A, ed
una coppia di autovalori
complessi coniugati di A, ed 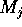 è un nilpotente con tutti i
coefficienti due diagonali sotto la diagonale principale uguali ad 1, e
gli altri nulli.
è un nilpotente con tutti i
coefficienti due diagonali sotto la diagonale principale uguali ad 1, e
gli altri nulli.
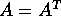 ammette una matrice
R ortogonale (con
ammette una matrice
R ortogonale (con 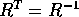 ) tale che
) tale che 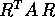 è una
matrice diagonale, con sulla diagonale gli autovalori, tutti
reali, di A.
è una
matrice diagonale, con sulla diagonale gli autovalori, tutti
reali, di A.
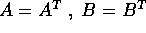 , tale
che almeno una delle due sia definita positiva, ammette una matrice
R invertibile che le diagonalizza simultaneamente, ossia tale che
sia
, tale
che almeno una delle due sia definita positiva, ammette una matrice
R invertibile che le diagonalizza simultaneamente, ossia tale che
sia 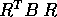 sono matrici diagonali.
sono matrici diagonali.