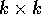 con il solo autovalore
con il solo autovalore 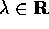 .
Allora la matrice
.
Allora la matrice
Sommario Se una matrice non è diagonalizzabile (e neppure semisemplice), essa differisce da una diagonalizzabile (o semisemplice) per una matrice che elevata a una qualche potenza dà la matrice zero. L'esponenziale di matrice può anche in questo caso essere espressa mediante funzioni analitiche elementari, tra cui appariranno, accanto a funzioni esponenziali, seni e coseni, anche dei polinomi.
Poiché le matrici con autovalori semplici sono diagonalizzabili o almeno semisemplici, cerchiamo un esempio di matrice non semisemplice all'estremo opposto, supponendo cioè che ci sia un solo autovalore di molteplicità massima, pari alla dimensione dello spazio.
Sia A una matrice 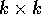 con il solo autovalore
con il solo autovalore 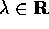 .
Allora la matrice
.
Allora la matrice

ha il solo autovalore 0, in particolare non è invertibile.
Consideriamo la trasformazione di 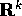 in sé associata ad N:
poiché non è un isomorfismo, l'immagine non è tutto
in sé associata ad N:
poiché non è un isomorfismo, l'immagine non è tutto 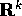 :
:

Ora applichiamo ancora N ad 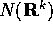 :
poiché anche la restrizione di N a questo sottospazio non ha
altri autovalori che lo 0, anche la restrizione non sarà un
isomorfismo, e quindi
:
poiché anche la restrizione di N a questo sottospazio non ha
altri autovalori che lo 0, anche la restrizione non sarà un
isomorfismo, e quindi 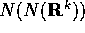 avrà una dimensione ancora più
bassa:
avrà una dimensione ancora più
bassa:
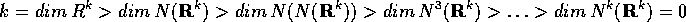
La sequenza di interi non negativi
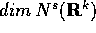 è strettamente decrescente, perciò deve
arrivare a 0 al più in k passi.
è strettamente decrescente, perciò deve
arrivare a 0 al più in k passi.
Definizione:
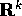 , ed anche
una matrice N ad esso associata, si dice nilpotente se esiste
un intero positivo s tale che
, ed anche
una matrice N ad esso associata, si dice nilpotente se esiste
un intero positivo s tale che

Il numero s si dice ordine del nilpotente ; per lo stesso
ragionamento visto sopra, l'ordine non può superare la
dimensione dello spazio ambiente: 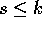 .
.
L'unico autovalore di un nilpotente è lo 0: se così non fosse,
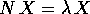 con
con 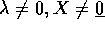 implicherebbe
implicherebbe
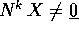 .
.
Viceversa, una matrice il cui unico autovalore è 0 è nilpotente.
Nel caso di una matrice A con un solo autovalore
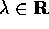 , la si può decomporre nella somma di una matrice
diagonale e di un nilpotente:
, la si può decomporre nella somma di una matrice
diagonale e di un nilpotente:

In questo caso il calcolo dell'esponenziale di matrice è
particolarmente semplice. Poiché 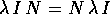 si
può applicare il teorema della somma degli esponenti :
si
può applicare il teorema della somma degli esponenti :
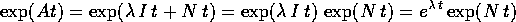
E se N è nilpotente, cioè 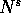 è la matrice zero (dove s
è l'ordine), la sua esponenziale è in realtà un polinomio di
grado s-1:
è la matrice zero (dove s
è l'ordine), la sua esponenziale è in realtà un polinomio di
grado s-1:
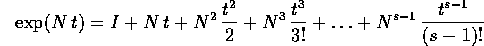
Possiamo concludere che le soluzioni del sistema dinamico lineare
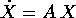 , con A che ha un solo autovalore, possono essere
espresse mediante prodotti della funzione esponenziale
, con A che ha un solo autovalore, possono essere
espresse mediante prodotti della funzione esponenziale
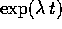 con polinomi in t; il grado dei polinomi è
minore della dimensione dello spazio (perché
con polinomi in t; il grado dei polinomi è
minore della dimensione dello spazio (perché 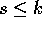 ).
).
Vogliamo cambiare base in modo da rendere la forma della matrice N
più semplice possibile. Prendiamo come primo vettore della nuova
base un vettore 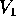 tale che
tale che 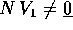 (esiste,
altrimenti N è la matrice zero), e come secondo vettore della base
(esiste,
altrimenti N è la matrice zero), e come secondo vettore della base
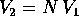 . Se
. Se 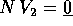 allora la sottomatrice
allora la sottomatrice
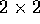 Q che esprime la trasformazione del sottospazio generato
da
Q che esprime la trasformazione del sottospazio generato
da 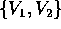 è della forma:
è della forma:
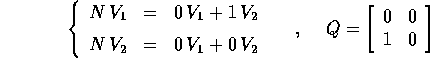
Se la dimensione k=2 allora questo è l'unico caso possibile; altrimenti il procedimento di riduzione in forma canonica del nilpotente va avanti, in uno dei due modi seguenti:
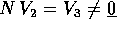 , nel qual caso si usa
, nel qual caso si usa 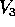 come terzo vettore della base; se
come terzo vettore della base; se 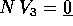 la
sottomatrice
la
sottomatrice 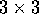 Q che esprime la trasformazione del
sottospazio generato da
Q che esprime la trasformazione del
sottospazio generato da 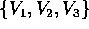 è:
è:
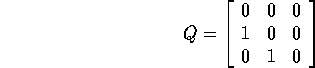
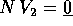 ; allora
scegliamo un terzo vettore della base
; allora
scegliamo un terzo vettore della base 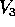 , indipendente da
, indipendente da
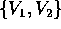 e tale che
e tale che 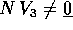 . Se questo
non è possibile, vuol dire che il resto della matrice è
zero; se è possibile, si inizia un nuovo blocco con le stesse
proprietà del primo.
. Se questo
non è possibile, vuol dire che il resto della matrice è
zero; se è possibile, si inizia un nuovo blocco con le stesse
proprietà del primo.
Questo ragionamento viene utilizzato nella dimostrazione
del teorema della forma canonica dei nilpotenti come passo
di induzione. È un procedimento costruttivo, che fornisce
esplicitamente la nuova base 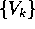 e quindi la matrice
e quindi la matrice 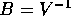 del cambiamento di coordinate lineare che riduce a forma canonica.
del cambiamento di coordinate lineare che riduce a forma canonica.
In generale una matrice nilpotente N di tipo 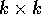 si può
ridurre, con un cambiamento di coordinate lineare
si può
ridurre, con un cambiamento di coordinate lineare 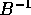 ,
nella forma descritta dal teorema della
forma canonica dei nilpotenti , cioè come matrice
diagonale a blocchi :
,
nella forma descritta dal teorema della
forma canonica dei nilpotenti , cioè come matrice
diagonale a blocchi :
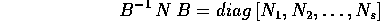
dove ciascun blocco di Jordan 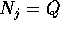 lungo la diagonale principale
ha la forma:
lungo la diagonale principale
ha la forma:
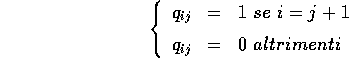
Esercizio
Per la matrice nilpotente Q definita sopra, calcolare
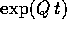 .
.
Suggerimento: 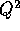 ha diversi da zero solo i coefficienti
di posto (i+2,i), se esistono;
ha diversi da zero solo i coefficienti
di posto (i+2,i), se esistono; 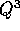 solo quelli di posto (i+3,i),
se esistono; e così via. Quindi nell'esponenziale il
coefficiente di posto (i+m+1,i) sarà
solo quelli di posto (i+3,i),
se esistono; e così via. Quindi nell'esponenziale il
coefficiente di posto (i+m+1,i) sarà 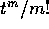 .
.
Se la matrice A ha un solo autovalore reale 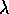 , è
della forma
, è
della forma 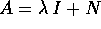 ; il cambiamento di coordinate lineare
che riduce il nilpotente N alla forma canonica non cambia
; il cambiamento di coordinate lineare
che riduce il nilpotente N alla forma canonica non cambia
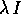 (che commuta con ogni matrice B), quindi riduce A
alla sua forma canonica di Jordan dove ciascun
blocco di Jordan F lungo la diagonale principale ha la forma:
(che commuta con ogni matrice B), quindi riduce A
alla sua forma canonica di Jordan dove ciascun
blocco di Jordan F lungo la diagonale principale ha la forma:
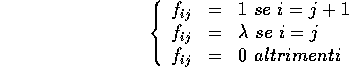
Dei vettori che formano la nuova base, soltanto il
primo di ogni blocco di Jordan è un autovettore
di autovalore 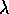 ; perciò il numero di blocchi di Jordan
nella forma canonica di un nilpotente è pari alla
molteplicità dell'autovalore .
; perciò il numero di blocchi di Jordan
nella forma canonica di un nilpotente è pari alla
molteplicità dell'autovalore .
Consideriamo il caso di dimensione k=2 ed una matrice A con un
solo autovalore reale 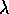 di molteplicità algebrica 2:
di molteplicità algebrica 2:
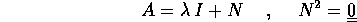
Supponiamo che la matrice A non sia diagonalizzabile, cioè che N non sia la matrice zero (altrimenti si ricade nel caso già visto in 2.3).
Poiché N è nilpotente, la sua esponenziale si riduce ad un polinomio di grado ordine - 1, in questo caso di grado 1:
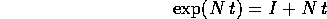
e poiché 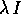 commuta con ogni altra matrice, inclusa N,
l'esponenziale della somma si può calcolare con il teorema
della somma degli esponenti :
commuta con ogni altra matrice, inclusa N,
l'esponenziale della somma si può calcolare con il teorema
della somma degli esponenti :
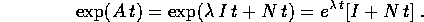
Quindi per il sistema dinamico lineare:
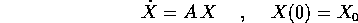
il flusso integrale
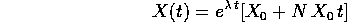
è esprimibile soltanto mediante l'esponenziale di esponente 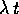 moltiplicata per polinomi di grado 1.
moltiplicata per polinomi di grado 1.
Come visto nello sottosezione precedente, cambiando riferimento
(cioè con un coniugio ), N può essere messo nella forma
canonica con un solo coefficiente diverso da zero sotto la diagonale.
Poiché il cambiamento di riferimento non cambia la matrice
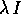 , nel nuovo riferimento la stessa applicazione è
espressa dalla matrice
, nel nuovo riferimento la stessa applicazione è
espressa dalla matrice 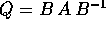 della forma
della forma
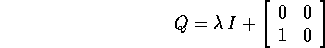
e quindi l'esponenziale è
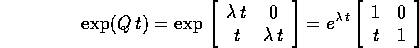
e la soluzione di 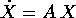 può essere espressa mediante la
matrice B del cambiamento di coordinate:
può essere espressa mediante la
matrice B del cambiamento di coordinate:
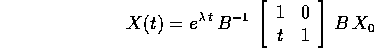
Questa formula è più semplice da esaminare dal punto di
vista qualitativo, ma in pratica è più complicata da usare di quella
precedente. Infatti per calcolare la matrice B occorre: scegliere un
vettore 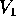 ; calcolare
; calcolare 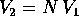 ; verificare che è diverso da
; verificare che è diverso da
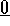 ; formare la matrice
; formare la matrice 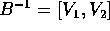 ; invertirla per
trovare B; eseguire le moltiplicazioni di matrici del coniugio con
B. Nella formula precedente invece basta calcolare
; invertirla per
trovare B; eseguire le moltiplicazioni di matrici del coniugio con
B. Nella formula precedente invece basta calcolare 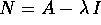 .
.
Esercizio
Trovare tutte le possibili matrici nilpotenti 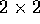 A e calcolarne
A e calcolarne
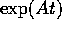 .
.
Suggerimento: se l'equazione caratteristica deve essere
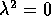 , poiché i coefficienti dell'equazione caratteristica
sono meno la traccia ed il determinante
(vedi 2.3):
, poiché i coefficienti dell'equazione caratteristica
sono meno la traccia ed il determinante
(vedi 2.3):

da cui 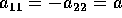 ; distinguendo i casi
; distinguendo i casi 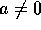 ed a=0...
ed a=0...
Il comportamento qualitativo delle orbite si può quindi studiare nel caso del sistema in forma canonica, a cui ci si può ricondurre con un cambiamento di coordinate lineare :
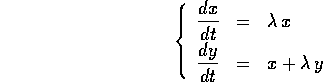
che è la generalizzazione dell'esempio
in 2.1; il flusso integrale, in funzione della
condizione iniziale 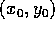 , è:
, è:
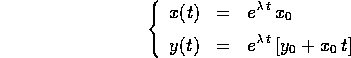
Il comportamento qualitativo dipende soltanto dal segno di 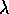 :
:
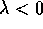 . Tutte le orbite per
. Tutte le orbite per 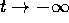 vanno all'infinito, e hanno come limite per
vanno all'infinito, e hanno come limite per 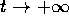 l'origine. Tendono all'origine con tangente
che tende alla verticale:
l'origine. Tendono all'origine con tangente
che tende alla verticale:
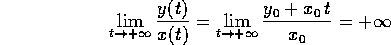
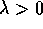 . Tutte le orbite per
. Tutte le orbite per 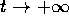 vanno all'infinito, e hanno come limite per
vanno all'infinito, e hanno come limite per 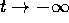 l'origine. Si allontanano dall'origine con tangente
verticale:
l'origine. Si allontanano dall'origine con tangente
verticale:
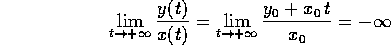
Nei due casi con 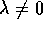 il comportamento qualitativo
attorno al punto di equilibrio si chiama
nodo improprio . Si noti la presenza di una
curva eccezionale che in questo caso è x=0.
il comportamento qualitativo
attorno al punto di equilibrio si chiama
nodo improprio . Si noti la presenza di una
curva eccezionale che in questo caso è x=0.
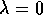 . Tutte le orbite tendono all'infinito per
. Tutte le orbite tendono all'infinito per
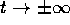 , salvo la linea di punti di
equilibrio per x=0. Ogni retta x=cost è un'orbita; per ogni
, salvo la linea di punti di
equilibrio per x=0. Ogni retta x=cost è un'orbita; per ogni
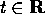 , il flusso integrale è uno scorrimento .
, il flusso integrale è uno scorrimento .
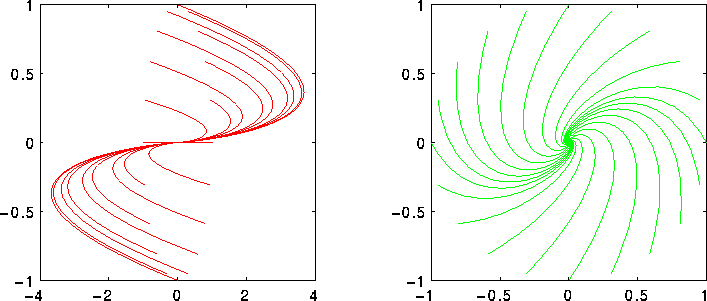
Figure 2.5: Nodo improprio con autovalore minore di zero; a sinistra in forma canonica.
Vogliamo ora delineare la procedura da usare per risolvere esplicitamente un sistema dinamico continuo lineare qualsiasi. Il procedimento applicabile in generale richiede di passare attraverso la decomposizione della matrice del sistema in somma di due matrici che commutano tra loro, e per ciascuna delle quali il calcolo dell'esponenziale è elementare.
Consideriamo il più generale sistema dinamico lineare :
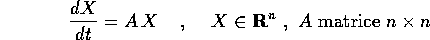
Per ogni matrice quadrata A il teorema della decomposizione S + N ci assicura che esistono una matrice semisemplice S ed una matrice nilpotente N tali che:
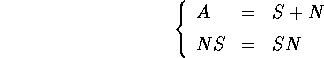
Questa decomposizione è unica, cioè sia S che N sono univocamente determinate da A.
Ne segue la possibilità di calcolare l'esponenziale di matrice che descrive il flusso integrale del sistema dinamico:
Teorema delle soluzioni del sistema dinamico lineare :
Per ogni matrice A di tipo 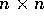 , tutte le orbite del
sistema dinamico continuo lineare
, tutte le orbite del
sistema dinamico continuo lineare 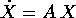 sono esprimibili
mediante combinazioni lineari di funzioni del tipo:
sono esprimibili
mediante combinazioni lineari di funzioni del tipo:
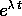 , dove
, dove 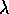 è un
autovalore reale di A;
è un
autovalore reale di A;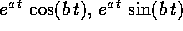 , dove
, dove 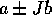 sono autovalori complessi di A;
sono autovalori complessi di A;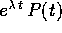 , dove
, dove 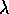 è un autovalore di A
di molteplicità algebrica
r e P(t) è un polinomio di grado
è un autovalore di A
di molteplicità algebrica
r e P(t) è un polinomio di grado 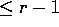 ;
;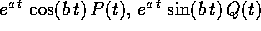 , dove
, dove
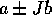 sono autovalori complessi di A di
molteplicità algebrica
r e P(t),Q(t) sono polinomi di grado
sono autovalori complessi di A di
molteplicità algebrica
r e P(t),Q(t) sono polinomi di grado 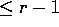 .
.
Dimostrazione:
In conseguenza della decomposizione S + N, sono possibili le seguenti semplificazioni nel calcolo dell'esponenziale di matrice :
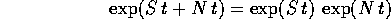
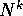 è la matrice zero e l'esponenziale di N è un polinomio
a coefficienti matrici di grado k-1:
è la matrice zero e l'esponenziale di N è un polinomio
a coefficienti matrici di grado k-1:
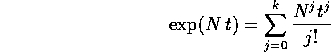
e quindi ogni suo coefficiente è un polinomio di grado non superiore a k.
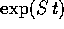 si esprime mediante
funzioni esponenziali, seni e coseni.
si esprime mediante
funzioni esponenziali, seni e coseni.
In realtà sia la decomposizione S+N, sia la forma canonica della matrice semisemplice S sono disponibili solo a condizione di conoscere tutti gli autovalori di A, il che non è affatto ovvio dal punto di vista computazionale.
Eseguendo la moltiplicazione di matrici 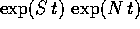 si
trovano le combinazioni lineari delle funzioni descritte
nell'enunciato del teorema.
si
trovano le combinazioni lineari delle funzioni descritte
nell'enunciato del teorema.
Resta solo da spiegare perché i polinomi che moltiplicano
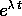 (oppure
(oppure 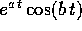 , o
, o
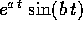 ) hanno grado non superiore alla
molteplicità dell'autovalore meno uno, benché appaiano nel
polinomio
) hanno grado non superiore alla
molteplicità dell'autovalore meno uno, benché appaiano nel
polinomio 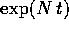 che ha un grado k che potrebbe essere
superiore. La dimostrazione di quest'ultimo punto richiederebbe una
discussione un po' più approfondita dei requisiti di algebra (vedi
Sezione B.1). Perciò la rimandiamo alla
seguente discussione sulle forme canoniche di Jordan.
che ha un grado k che potrebbe essere
superiore. La dimostrazione di quest'ultimo punto richiederebbe una
discussione un po' più approfondita dei requisiti di algebra (vedi
Sezione B.1). Perciò la rimandiamo alla
seguente discussione sulle forme canoniche di Jordan.
Una descrizione più esplicita, almeno dal punto di vista geometrico, del flusso integrale di un sistema dinamico lineare generale può essere ottenuta utilizzando la forma canonica di Jordan e la forma canonica di Jordan reale . Se la matrice A ha solo autovalori reali, esiste un cambiamento di coordinate lineare B tale che:
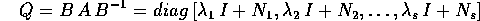
dove 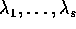 sono gli autovalori distinti di
A, di molteplicità algebrica
sono gli autovalori distinti di
A, di molteplicità algebrica
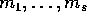 , ed
, ed 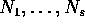 sono matrici nilpotenti
operanti su spazi di dimensioni pari alle molteplicità algebriche
rispettive.
sono matrici nilpotenti
operanti su spazi di dimensioni pari alle molteplicità algebriche
rispettive.
Questo completa la dimostrazione del teorema delle
soluzioni del sistema dinamico lineare
nel caso di autovalori
reali, perché il nilpotente 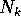 ha ordine
ha ordine 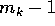 , e quindi la
corrispondente esponenziale viene moltiplicata per un polinomio di
grado non superiore a
, e quindi la
corrispondente esponenziale viene moltiplicata per un polinomio di
grado non superiore a 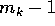 .
.
Inoltre si può scegliere la nuova base, cioè la matrice 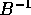 ,
in modo tale che ciascuno dei nilpotenti
,
in modo tale che ciascuno dei nilpotenti 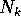 abbia la
forma canonica dei nilpotenti (si vedano gli esempi
nella Sezione 2.5); allora la matrice trasformata Q
sarà diagonale a blocchi , con un certo numero di
blocchi di Jordan per ogni autovalore
distinto:
abbia la
forma canonica dei nilpotenti (si vedano gli esempi
nella Sezione 2.5); allora la matrice trasformata Q
sarà diagonale a blocchi , con un certo numero di
blocchi di Jordan per ogni autovalore
distinto:
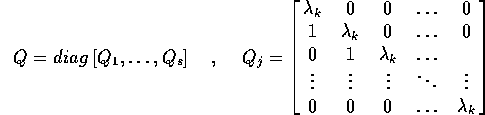
Questa è la forma canonica di Jordan di una matrice ad
autovalori reali. L'esponenziale di una matrice Q in forma canonica
di Jordan è diagonale a blocchi, con le esponenziali dei blocchi di
Jordan lungo la diagonale. Se il blocco di Jordan 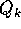 è di tipo
è di tipo
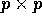 :
:
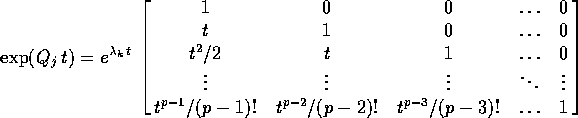
Una descrizione analoga è possibile nel caso in cui A abbia anche
autovalori complessi coniugati, utilizzando la
forma canonica di Jordan reale .
In un opportuno sistema di riferimento ad ogni coppia di autovalori
complessi coniugati 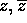 corrisponde un certo numero di
blocchi di Jordan reali della
forma:
corrisponde un certo numero di
blocchi di Jordan reali della
forma:
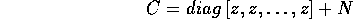
dove z è rappresentato dalla sua forma matriciale 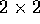 ed il nilpotente N ha la forma
ed il nilpotente N ha la forma
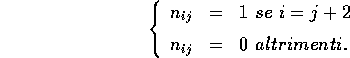
Si noti che 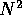 ha diversi da zero solo i coefficienti di posto
i+4,i (se esistono).
ha diversi da zero solo i coefficienti di posto
i+4,i (se esistono).
Per completare la dimostrazione del teorema
delle soluzioni del sistema dinamico lineare occorre considerare
che i blocchi di Jordan reali associati agli autovalori 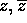 non possono essere più grandi di
non possono essere più grandi di 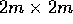 se m è la
molteplicità algebrica
della coppia di autovalori.
se m è la
molteplicità algebrica
della coppia di autovalori.
Esercizio Determinare esplicitamente il flusso integrale del sistema dinamico
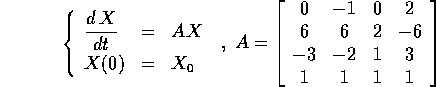
e studiare i limiti delle traiettorie per 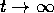 .
.
Suggerimento: Si possono evitare i noiosi calcoli del polinomio caratteristico sapendo che la matrice data ha un solo autovalore ... ?
Vogliamo discutere un esempio di sistema dinamico lineare con una matrice ad autovalori non reali e non semisemplice. Questo esempio è concettualmente importante, essendo il più semplice possibile esempio di risonanza , cioè di effetti di amplificazione dovuti all'eguaglianza di due frequenze, in un sistema dinamico.
Esempio:
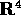 :
:
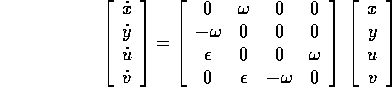
Si ottiene dall'accoppiamento di due oscillatori armonici .
La matrice A del sistema è decomponibile nella forma S+N, con
la parte semisemplice 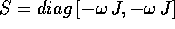 (si noti il
segno meno), mentre la parte nilpotente N ha due soli coefficienti
diversi da zero, ed uguali ad
(si noti il
segno meno), mentre la parte nilpotente N ha due soli coefficienti
diversi da zero, ed uguali ad  , nei posti
, nei posti 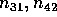 ;
;
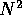 è la matrice zero. L'esponenziale di matrice si calcola
separatamente per S ed N:
è la matrice zero. L'esponenziale di matrice si calcola
separatamente per S ed N:
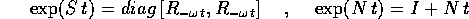
dove 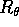 è la rotazione di un angolo
è la rotazione di un angolo 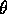 nel piano
nel piano
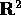 , in verso antiorario se
, in verso antiorario se 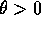 (quindi la rotazione è
in verso orario se
(quindi la rotazione è
in verso orario se 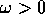 ).
).
Importante: per poter usare il teorema della somma degli esponenti bisogna verificare che SN=NS; non è detto che sia così per ogni modo di scomporre la matrice in semisemplice più nilpotente, ma in questo caso è vero, cioè la decomposizione descritta qui sopra è una di quelle del teorema della decomposizione S + N .
Allora l'orbita con condizione iniziale
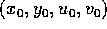 è:
è:
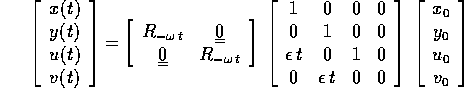
ossia la soluzione (x(t),y(t)) è quella dell'oscillatore armonico, mentre per (u(t),v(t)):
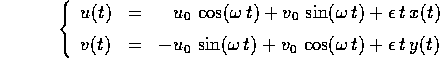
La proprietà notevole di questo flusso integrale è che le soluzioni sono illimitate, cioè l'accoppiamento di due oscillatori armonici risulta in un trasferimento illimitato di energia.