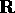 , ma non sempre
tendono ad un punto limite: i valori limite possono formare degli
insiemi limite non banali. Però non tutti gli insiemi possono essere
insiemi limite, perché devono soddisfare alcune proprietà
topologiche.
, ma non sempre
tendono ad un punto limite: i valori limite possono formare degli
insiemi limite non banali. Però non tutti gli insiemi possono essere
insiemi limite, perché devono soddisfare alcune proprietà
topologiche.
Sommario Le soluzioni che non `escono' dall'insieme di definizione
del campo vettoriale sono definite per ogni t in 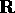 , ma non sempre
tendono ad un punto limite: i valori limite possono formare degli
insiemi limite non banali. Però non tutti gli insiemi possono essere
insiemi limite, perché devono soddisfare alcune proprietà
topologiche.
, ma non sempre
tendono ad un punto limite: i valori limite possono formare degli
insiemi limite non banali. Però non tutti gli insiemi possono essere
insiemi limite, perché devono soddisfare alcune proprietà
topologiche.
Il teorema della continuazione delle soluzioni assicura
che una soluzione di un sistema dinamico continuo, definito
(e di classe 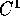 ) su di un aperto
) su di un aperto 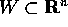 , o è definita
per ogni t abbastanza grande, oppure esce definitivamente per
, o è definita
per ogni t abbastanza grande, oppure esce definitivamente per
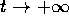 da ogni compatto
da ogni compatto 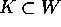 . Analogamente per
. Analogamente per
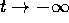 . Supponiamo che una certa soluzione X(t) resti sempre
dentro un compatto
. Supponiamo che una certa soluzione X(t) resti sempre
dentro un compatto 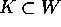 ; dunque possiamo assumere che essa sia
un'orbita , cioè sia definita per ogni t in
; dunque possiamo assumere che essa sia
un'orbita , cioè sia definita per ogni t in 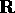 ; ma
allora tutte le successioni di punti
; ma
allora tutte le successioni di punti 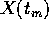 con
con 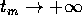 devono avere delle sottosuccessioni convergenti, cioè devono
esistere dei valori limite della funzione X(t) per
devono avere delle sottosuccessioni convergenti, cioè devono
esistere dei valori limite della funzione X(t) per 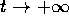 (lo
stesso per
(lo
stesso per 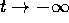 ).
).
L'insieme dei valori limite di un'orbita non cambia se si sceglie
una diversa condizione iniziale 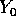 che si trova lungo la stessa
traiettoria :
che si trova lungo la stessa
traiettoria : 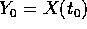 per qualche
per qualche 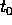 in
in 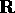 , poiché
se Y(t) è l'orbita con condizione iniziale
, poiché
se Y(t) è l'orbita con condizione iniziale 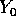 , allora
per l'unicità della soluzione con condizione iniziale data
, allora
per l'unicità della soluzione con condizione iniziale data 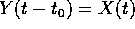 .
.
Definizione:
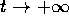 si chiama
insieme
si chiama
insieme 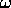 -limite dell'orbita. L'insieme dei
valori limite per
-limite dell'orbita. L'insieme dei
valori limite per 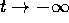 si chiama
insieme
si chiama
insieme 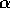 -limite .
Gli uni e gli altri si indicano anche
con il nome di insiemi limite quando non importa distinguere i
due casi.
-limite .
Gli uni e gli altri si indicano anche
con il nome di insiemi limite quando non importa distinguere i
due casi.
Se l'orbita `va all'infinito', cioè non è limitata, gli
insiemi 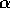 -limite ed
-limite ed 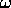 -limite possono essere vuoti. Lo
stesso può accadere se l'orbita tende al bordo dell'insieme su cui
il sistema dinamico è definito.
-limite possono essere vuoti. Lo
stesso può accadere se l'orbita tende al bordo dell'insieme su cui
il sistema dinamico è definito.
Teorema di invarianza degli insiemi limite :
Dato un sistema dinamico continuo su W aperto di 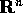 , se L
è l'insieme
, se L
è l'insieme 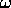 -limite di una soluzione
-limite di una soluzione 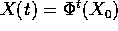 ,
allora:
,
allora:
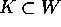 , allora L è un insieme connesso .
, allora L è un insieme connesso .
Gli insiemi 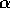 -limite hanno le stesse proprietà (a), (b) e (c).
-limite hanno le stesse proprietà (a), (b) e (c).
Dimostrazione:
(a) Tutti gli insiemi limite (di qualunque
successione o funzione) sono chiusi: in questo caso sia 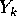 (per
ogni
(per
ogni 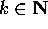 ) un punto limite in L, cioè esista una successione
) un punto limite in L, cioè esista una successione
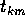 che tende a
che tende a 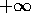 per
per 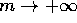 , tale che
, tale che
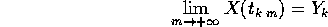
e a sua volta la successione di punti limite 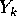 tenda a Y per
tenda a Y per
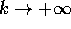 ; allora per ogni
; allora per ogni  esiste un m(k)
tale che
esiste un m(k)
tale che
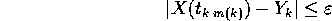
da cui per l'unicità del limite di una successione
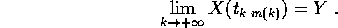
ossia Y appartiene ad L.
(b) Sia 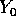 un punto dell'
un punto dell' 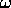 -limite L, cioè esista una
successione
-limite L, cioè esista una
successione 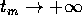 tale che:
tale che:
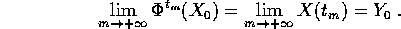
dove 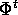 è il flusso integrale. Allora, se
è il flusso integrale. Allora, se
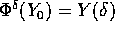 è un qualsiasi altro punto
dell'orbita per
è un qualsiasi altro punto
dell'orbita per 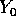 ,
,
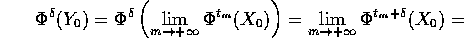
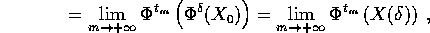
cioè anche 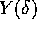 è un punto dell'insieme
è un punto dell'insieme 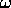 -limite L.
-limite L.
Abbiamo utilizzato due proprietà del flusso integrale: di essere una funzione continua delle condizioni iniziali e di essere un gruppo ad un parametro con parametro t.
(c) Supponiamo che L possa essere diviso in due parti 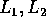 tali che esistono due aperti disgiunti
tali che esistono due aperti disgiunti 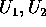 con
con 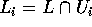 ; allora esistono due successioni
; allora esistono due successioni 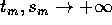 tali che
tali che
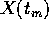 tende ad un punto di
tende ad un punto di 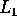 ed
ed 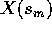 tende ad un punto di
tende ad un punto di
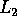 , per cui
, per cui 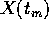 sta definitivamente in
sta definitivamente in 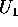 ed
ed 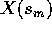 sta
definitivamente in
sta
definitivamente in 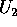 .
.
Allora esiste una terza successione 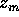 con
con 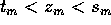 tale che
tale che 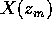 non sta né in
non sta né in 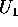 né in
né in
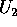 .
. 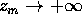 . La successione
. La successione 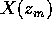 (che è
contenuta nel compatto K) ha almeno un punto limite che non sta
né in
(che è
contenuta nel compatto K) ha almeno un punto limite che non sta
né in 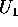 né in
né in 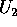 , ma è un punto dell'insieme
, ma è un punto dell'insieme
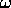 -limite L; da qui la contraddizione.
-limite L; da qui la contraddizione.
Per gli insiemi 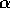 -limite si possono usare gli analoghi
argomenti per
-limite si possono usare gli analoghi
argomenti per 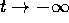 .
.
Benché il teorema che precede indichi delle proprietà
importanti, tuttavia queste non sono
sufficienti a caratterizzare gli insieme limite: si possono costruire
degli insiemi chiusi, invarianti ed anche connessi che non possono
essere insieme limite di alcun sistema dinamico. La ricerca di una
caratterizzazione degli insieme limite è molto difficile, e una
soluzione completa di questo problema si può dare solo in 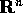 con
con
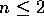 , come si vedrà nella Sezione 3.8.
, come si vedrà nella Sezione 3.8.
Possiamo ora svolgere la dimostrazione che avevamo lasciato in sospeso nella Sezione 3.4, cioè quella del teorema della funzione di Lyapounov decrescente , che era stata differita proprio per poter utilizzare la nozione di insieme limite:
Dimostrazione:
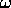 -limite di un'orbita contenuta
nell'insieme positivamente invariante P. Allora
-limite di un'orbita contenuta
nell'insieme positivamente invariante P. Allora 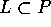 (perché quest'ultimo è chiuso ).
Sia
(perché quest'ultimo è chiuso ).
Sia 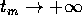 una successione
tale che
una successione
tale che
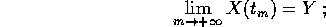
allora 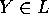 e per continuità della funzione di Lyapounov V:
e per continuità della funzione di Lyapounov V:
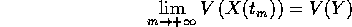
ma poiché V è non crescente tale limite deve anche essere il
minimo limite per 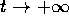 di V(X(t)), e quindi non
dipende dalla scelta di Y in L. Allora V è costante su L,
e dall'ipotesi su P segue che L coincide con il punto di
equilibrio S, che è asintoticamente stabile con bacino
contenente almeno P.
di V(X(t)), e quindi non
dipende dalla scelta di Y in L. Allora V è costante su L,
e dall'ipotesi su P segue che L coincide con il punto di
equilibrio S, che è asintoticamente stabile con bacino
contenente almeno P.
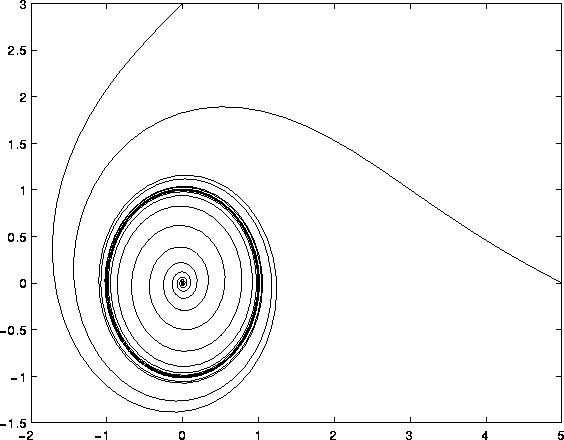
Figure 3.13: Orbita periodica che funge da ciclo limite
Definizione:
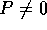 tale che
tale che

per ogni t in  . Il più piccolo di tali P si dice periodo
dell'orbita periodica.
. Il più piccolo di tali P si dice periodo
dell'orbita periodica.
Un punto di equilibrio ha ``periodo zero'' e non è considerato un'orbita periodica.
Per le orbite periodiche ogni punto della traiettoria è un valore limite:
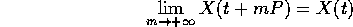
quindi l'insieme 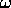 -limite
coincide con la traiettoria, e così
l'insieme
-limite
coincide con la traiettoria, e così
l'insieme 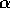 -limite .
-limite .
L'insieme dei punti percorsi da un'orbita periodica può anche
fungere da insieme 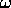 -limite (oppure
-limite (oppure 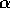 -limite) per
un'orbita diversa; in tal caso si parla di ciclo limite , come
nell'esempio nella Figura 3.13.
-limite) per
un'orbita diversa; in tal caso si parla di ciclo limite , come
nell'esempio nella Figura 3.13.