In un sistema dinamico continuo, se una soluzione ha un limite
finito per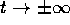 
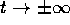, questo limite sarà un punto di
equilibrio. Un punto di equilibrio è considerato stabile se tutte le
soluzioni ad essa vicine restano vicine, asintoticamente stabile se
hanno anche lo stesso limite finito. La stabilità, ed il
comportamento qualitativo delle soluzioni nell'intorno di un punto di
equilibrio, possono essere determinate mediante lo studio
dell'approssimazione lineare nel punto stesso, oppure mediante la
costruzione di una funzione di Lyapounov. Quando non esiste un unico
punto limite, l'insieme dei valori limite ha comunque delle
proprietà forti, che consentono di caratterizzare completamente i
possibili insiemi limite nel piano.