8.6 EQUAZIONI ALLE VARIAZIONI

 

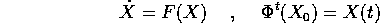
Sommario La matrice jacobiana del flusso integrale può essere ottenuta come soluzione di un'equazione lineare a coefficienti dipendenti dal tempo, l'equazione alle variazioni. Quest'ultima può essere sfruttata per studiare le proprietà del flusso integrale che dipendono dal suo differenziale; tra queste c'è anche la proprietà di essere una trasformazione canonica.

Dato un sistema dinamico ed il suo flusso integrale:

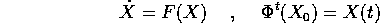
limitiamoci a considerare un ``piccolo'' intorno di una singola soluzione 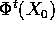. Piccolo vuol dire che la soluzione ``variata'' Y(t) avrà condizione iniziale 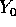che tende ad 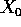, e considereremo trascurabili i termini del secondo ordine di infinitesimo rispetto a 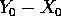. Poiché il flusso integrale è continuo rispetto alle condizioni iniziali, sarà ancora vero che 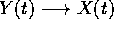almeno per t in un intervallo limitato. Allora l'equazione del moto relativo:

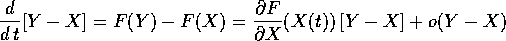
si può linearizzare trascurando gli infinitesimi di ordine superiore; il vettore ``variazione'' V=Y-X soddisferà ad un'equazione differenziale lineare a coefficienti variabili:

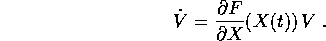
Questa argomentazione può essere resa rigorosa utilizzando il teorema di differenziabilità del flusso , per cui il flusso integrale è differenziabile (di classe almeno 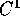) rispetto alle condizioni iniziali, e dotato di derivate miste continue:

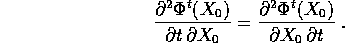
Allora chiamiamo 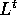la matrice jacobiana del flusso integrale rispetto alle condizioni iniziali, calcolata per le condizioni iniziali 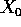date:

e deriviamo rispetto alle condizioni iniziali il primo membro dell'equazione di moto, in cui è stato sostituito :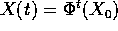

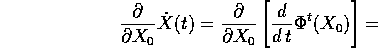
sfruttando l'eguaglianza delle derivate miste, si può scambiare la derivata rispetto a t con quella rispetto alle condizioni iniziali

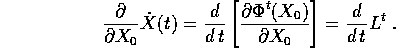
Eseguendo gli stessi calcoli sul secondo membro dell'equazione differenziale:

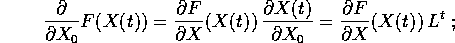
ed eguagliando

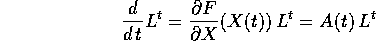
si ottiene un'equazione lineare, detta equazione alle variazioni  , la cui matrice dei coefficienti A(t) dipende dal tempo (in modo continuo, essendo la matrice jacobiana della F(x) calcolata lungo la soluzione data).

Poiché il flusso integrale al tempo zero è l'identità:

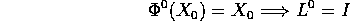
ne segue che la matrice 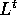è proprio la matrice ottenuta accostando un sistema fondamentale di soluzioni  dell'equazione alle variazioni.

Esempio:

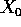Se è un punto di equilibrio: 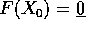, allora l'equazione alle variazioni è a coefficienti costanti, e coincide con il sistema linearizzato:



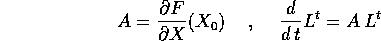
con sistema di soluzioni fondamentali .

Esempio:

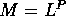Se X(t) è una soluzione periodica di periodo P, allora l'equazione alle variazioni è a coefficienti periodici di periodo P. La matrice di monodromia   descrive la stabilità della soluzione periodica.

Problema Nel caso di un'orbita periodica, dimostrare che la matrice di monodromia M è della forma 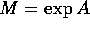, dove A è una matrice quadrata. Mostrare che la stabilità dell'orbita periodica dipende dal segno delle parti reali degli autovalori di A, che sono pure detti esponenti di Lyapounov .

Flussi canonici

Data una hamiltoniana H(P,Q), le equazioni di Hamilton  si possono mettere nella forma:

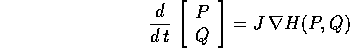
dove J è la matrice che definisce la struttura simplettica  dello spazio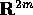

Se indichiamo con 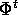il flusso integrale di questo sistema hamiltoniano, allora 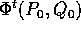è una soluzione delle equazioni di Hamilton, cioè come funzione di t soddisfa al problema alle condizioni iniziali

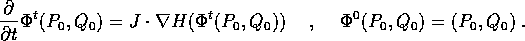
Consideriamo ora lo stesso flusso integrale 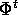come una trasformazione dello spazio (P,Q), cioè come un'applicazione

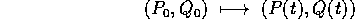
tra le condizioni iniziali e lo stato al tempo t. Per il teorema di differenziabilità possiamo derivare rispetto alle componenti delle condizioni iniziali, e costruire la matrice jacobiana (di tipo )

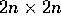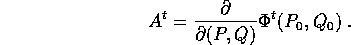
Possiamo allora costruire l'equazione alle variazioni  prendendo la matrice jacobiana dei due membri dell'equazione differenziale soddisfatta da 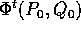: al primo membro, scambiando l'ordine di derivazione:

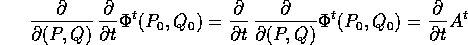
e al secondo membro

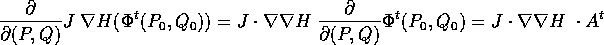
dove è stata usata la regola di differenziazione delle funzioni composte, e dove 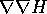è la matrice hessiana delle derivate seconde, che è simmetrica; si intende che essa va calcolata lungo l'orbita 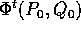. Dunque 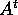, l'evoluzione della matrice jacobiana del flusso lungo l'orbita con una fissa condizione iniziale, se considerata come funzione del solo t è la soluzione del problema alle condizioni iniziali:

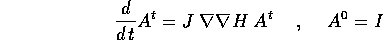
che è un sistema di equazioni differenziali lineari non autonome: i coefficienti sono una funzione di t che è nota, una volta che sia nota l'orbita .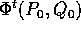

Le equazioni alle variazioni qua sopra sono a loro volta equazioni di Hamilton, nel senso che la matrice 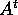rappresenta un sistema fondamentale di soluzioni delle equazioni con hamiltoniana quadratica dipendente dal tempo:

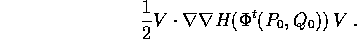
Teorema del flusso canonico :  Data una funzione hamiltoniana H(P,Q) di classe 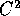, sia 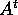la soluzione dell'equazione alle variazioni che fornisce la matrice jacobiana del

flusso integrale lungo una soluzione (P(t),Q(t)). La 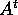è, per ogni t per cui è definita, una matrice simplettica , cioè di soddisfa a

Dimostrazione:

Sia



allora C è la soluzione del problema alle condizioni iniziali, che si ottengono sostituendo alla derivata di 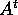il secondo membro dell'equazione alle variazioni:





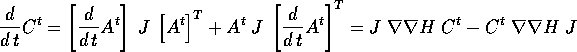
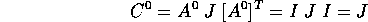
che ha la soluzione ovvia 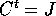; per unicità della soluzione, 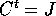e quindi 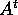è simplettica.

 C.D.D.

Come già osservato nel caso ad un grado di libertà, questo risultato corrisponde alla nozione intuitiva che il flusso integrale è canonico, in quanto conserva la forma hamiltoniana delle equazioni di moto, che sono indipendenti dal tempo e perciò invarianti rispetto allo scorrere del tempo stesso.

Peraltro la dimostrazione qui sopra della canonicità del flusso si applica anche al caso di una hamiltoniana dipendente dal tempo; la dipendenza dal tempo appare nell'equazione alle variazioni soltanto in 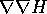, che comunque dipende dal tempo attraverso le soluzioni.

Definizione:

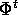Un sistema dinamico sullo spazio delle fasi di coordinate (P,Q) si dice conservativo   se il suo flusso integrale , inteso come trasformazione dello spazio delle fasi per t fisso, è una trasformazione canonica.

Per il teorema qui sopra, ogni sistema dinamico definito da equazioni di Hamilton è conservativo.

Questa definizione di sistema dinamico conservativo generalizza la definizione di sistema dinamico conservativo  data nel caso ad un grado di libertà; infatti le trasformazioni che conservano l'area , nel caso in cui lo spazio delle fasi ha dimensione 2, coincidono con le trasformazioni canoniche.

Questa definizione giustifica anche l'uso dell'espressione ``sistema conservativo'' anche se applicata ad un sistema newtoniano conservativo . Benché il sistema dinamico associato alle equazioni di Newton, e anche alle corrispondenti equazioni di Lagrange , non sia conservativo nel senso della definizione qua sopra, esiste pur sempre un corrispondente sistema hamiltoniano, ottenuto per trasformazione di Legendre , che ha questa proprietà.