1.4 NOTAZIONI E INDICI

Sommario Descriviamo i sistemi di indicizzazione e di legami ipertestuali che possono essere usati per orientarsi nella lettura di questo testo. Riassumiamo inoltre le principali notazioni usate in tutto il libro.

Indici e legami ipertestuali

Per ogni nozione introdotta in questo testo, che possa essere contraddistinta da una o più parole chiave, di regola esiste un unico punto in cui viene fornita una definizione. Si noti che non in tutti i casi la parola definizione appare esplicitamente; può anche essere data contestualmente ad una discussione, dimostrazione, esempio. I risultati più importanti, che secondo me meritano il titolo di teoremi (si badi che questa valutazione è sempre soggettiva), sono pure indicati dalle parole chiave che costituiscono il nome del teorema.

Ogni volta che una definizione, o un teorema, viene richiamato nel testo, il legame ipertestuale viene reso attivo e può essere acceduto toccando con il mouse le parole chiave. Inoltre ogni punto in cui viene richiamata una definizione o teorema è indicato nell'indice analitico.

Perciò questo testo può essere letto sequenzialmente, oppure usato come ipertesto seguendo i legami ipertestuali ogni volta che sia necessario richiamare o chiarire una nozione, oppure consultato attraverso l'indice analitico, e questo in ciascuna delle due versioni, cartacea e World Wide Web.

Scelta delle notazioni

Si noti che non è praticamente possibile, in un testo di queste dimensioni, usare in modo coerente sempre la stessa lettera per indicare uno ed un solo tipo di oggetto. Perciò molto difficilmente uno stesso simbolo segue una convenzione applicabile in più di un capitolo.

Fanno eccezione, cioè sono veramente simboli globali, i simboli usati per indicare campi numerici:

${\bf R}, {\bf Z}, {\bf C}, {\bf Q}, {\bf N}$ numeri reali, interi, complessi, razionali, naturali. ${\bf T}^n$ toro $n$-dimensionale.

Per i numeri complessi si alternano due notazioni: l'unità reale può essere indicata come $1$ o come $I$, l'unità immaginaria come $i$ o come $J$ (questo deriva dalla forma matriciale dei numeri complessi, vedi Sezione 2.4).

Notazioni vettoriali e matriciali

La scelta delle notazioni è dettata soprattutto dall'esigenza di rendere semplice il passaggio da una a più variabili; per esempio usando sistematicamente la moltiplicazione di scalari e la moltiplicazione di matrici (righe per colonne) senza distinzioni di notazione.

Vettori e matrici sono sempre indicati con lettere maiuscole; i loro coefficienti con le corrispondenti lettere minuscole ed i relativi indici:

$$X=(x_i)_{i=1,n}\in {\bf R}^n\mbox{\ oppure } \in {\bf C}^n$$

$$A=(a_{ik})_{i=1,n;k=1,r}\in \mbox{ matrici di tipo } n\times r$$

I vettori si intendono vettori colonna se non viene indicato altrimenti; tuttavia all'interno di un paragrafo di testo si scrive come un vettore riga anche quello che va interpretato come un vettore colonna: $(x,y)\in {\bf R}^2$.

Vettore e matrice zero:

$$\underline{0}\hspace{5mm},\hspace{5mm}{\underline{\underline{0}}}$$

$$A=B\, C \mbox{\ prodotto righe per colonne; } A^T \mbox{\ matrice trasposta}$$

Matrici diagonali e diagonali a blocchi:

$$D=diag\,[\lambda_1, \lambda_2,\ldots,\lambda_n]=(d_{ik})\ con\ d_{ik}=0 \ per\ i\neq k \mbox{\ matrice diagonale}$$

$$Q=diag\,\left[\lambda_1,\ldots,\lambda_n,\left[\begin{array}... ...nd{array}\right]\right] \ \ \mbox{matrice diagonale a blocchi}$$

Derivate

Derivate totali (cioè lungo le soluzioni del sistema dinamico continuo) rispetto al tempo:

$$\dot X = \frac{d{X}}{d{t}} \hspace{5mm},\hspace{5mm}\ddot X = \frac{d^2{X}}{d{t}^2}$$

Le derivate parziali di una funzione scalare $f(X)$ formano il vettore gradiente, che fa eccezione alla convenzione citata sopra perché è sempre un vettore riga:

$$grad\, f=\frac{\partial {f}}{\partial {X}}= \left[\frac{\par... ...rtial {x_2}},\ldots,\frac{\partial {f}}{\partial {x_n}}\right]$$

mentre il gradiente come vettore colonna viene indicato con un altro simbolo:

$$(grad\,f)^T=\nabla f\;.$$

La matrice jacobiana, formata con le derivate parziali di una funzione vettoriale $F\;:\; {\bf R}^n \; \longrightarrow \; {\bf R}^m$, viene sempre scritta con i gradienti come righe, e quindi è di tipo $m\times n$; si usa la notazione delle derivate parziali con argomento vettoriale:

$$\frac{\partial {F}}{\partial {X}} = \left(\frac{\partial {f_i}}{\partial {x_j}}\right)\ ,\ i=1,\ldots,m\,,\; j=1,\ldots,n \;;$$

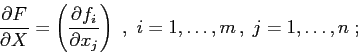
In questo modo la matrice jacobiana della funzione composta si indica nel modo più naturale come prodotto di matrici:

$$Z=F(Y)=F(G(X)) \Longrightarrow \frac{\partial {Z}}{\partial ... ...rtial {F}}{\partial {Y}}\,\frac{\partial {G}}{\partial {X}}\;.$$