3.8 TEOREMA DI POINCARÉ-BENDIXON

Sommario Nel piano ${\bf R}^2$ si possono caratterizzare tutti gli insiemi $\omega$-limite ed $\alpha$-limite, che o contengono punti di equilibrio o sono cicli limite. Questo teorema non vale né su altre varietà di dimensione 2 né in ${\bf R}^n$ per $n>2$, dove la situazione può essere molto più complicata.

Sezioni locali

Ci limitiamo in questa sezione a considerare sistemi dinamici in ${\bf R}^2$. Sia $F(X)$ il campo vettoriale su un aperto $W\subset {\bf R}^2$ che definisce il sistema dinamico, e prendiamo un qualunque punto $X_0$ di $W$ che non sia un equilibrio, cioè tale che $F(X_0)\neq \underline 0$. Allora per $X_0$ passa una soluzione $X(t)$ (con $X(0)=X_0$).

Definizione:

Una sezione locale del sistema dinamico è una curva $C^1$ $g:I\to W$ definita su un intervallo $I\subset {\bf R}$ tale che in ogni punto $g(s)$, la velocità $dg/ds$ della curva è linearmente indipendente dal campo vettoriale $F$.

In altre parole, la sezione locale attraversa trasversalmente tutte le soluzioni del sistema dinamico che incontra.

In particolare una sezione locale non può passare per un punto di equilibrio.

Proprietà:

Per ogni punto di $W$ che non è di equilibrio passa almeno una sezione locale (in effetti più d'una): per esempio una retta perpendicolare in $X_0$ al vettore $F(X_0)$ resta trasversale alle soluzioni almeno in un intorno di $X_0$.

Se $S$ è l'immagine di una sezione locale, esiste un intorno $U$ di $S$ tale che tutte le soluzioni passanti dentro $U$ devono necessariamente incontrare anche $S$. Infatti la distanza da $S$ (con segno, tenendo conto dell'orientazione) ha derivata diversa da zero su $S$ e (per continuità) su un suo intorno, e deve quindi passare dal valore zero.

Una descrizione più precisa del comportamento delle soluzioni in un intorno di una sezione locale può essere ottenuta per mezzo del teorema di continuità del flusso, grazie al quale si può dare a tale intorno una struttura prodotto.

Figura 3.13: I successivi incontri di una soluzione con una sezione locale. La curva $C$ che va da $X_0$ a $X_1$ lungo la soluzione $X(t)$, e poi da $X_1$ ad $X_0$ lungo una sezione locale, è una curva continua chiusa e quindi la stessa soluzione $X(t)$ resta intrappolata all'interno o all'esterno, a seconda della posizione relativa di $X_0$ ed $X_1$ sulla sezione locale, ma in entrambe una terza intersezione $X_2$ deve essere tale che $X_1$ sta tra $X_0$ ed $X_2$.

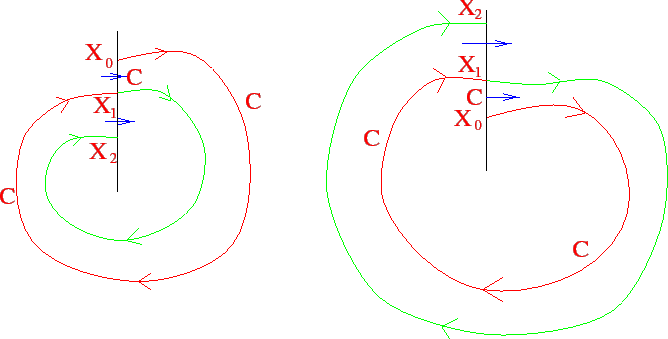
La teoria qualitativa dei sistemi dinamici continui nel piano è resa relativamente facile dal fatto che ci sono forti restrizioni, dovuti alle proprietà topologiche del piano, alla maniera in cui una stessa orbita può incontrare ripetutamente una sezione locale. Supponiamo che $g$ sia una sezione locale in $X_0$, con $g(s_0)=X_0$, e che $X(t)$ sia una soluzione tale che $X(0)=X_0$; per qualche $t_1>0$ sia inoltre $X(t_1)=X_1$ un punto che incontra la stessa sezione locale $g$, cioè esista un altro valore $s_1$ del parametro $s\in I$ tale che $g(s_1)=X_1$; supponiamo infine $s_1>s_0$. Consideriamo allora la figura formata dalla curva soluzione $X(t)$ per $0\leq t\leq t_1$ e dalla sezione locale per $s_0\leq s \leq s_1$: si tratta di una curva chiusa $C$, differenziabile a tratti (vedi Figura 3.13).

Si applica quindi il teorema della curva di Jordan, per cui ${\bf R}^2-C$ è diviso in due componenti connesse: l'interno $D$, e l'esterno $E$ (rispetto alla curva $C$). Una qualsiasi curva continua non può uscire da $D$ senza passare per $C$. In particolare una curva soluzione, come la curva $X(t)$ stessa, una volta che si trovi dentro $D$ non può uscirne che dal tratto $X_1X_0$ della sezione locale. Però, la sezione essendo trasversale, le soluzioni che passano da questo segmento o entrano tutte o escono tutte da $D$; se la soluzione $X(t)$ entra dentro $D$, non può più uscirne per valori maggiori di $t$; se esce, non può rientrare. Se ne deduce il lemma della sequenza monotona:

Lemma:

Sia $g:I\to W$ è una sezione locale, con $I\subset {\bf R}$ un intervallo, $X_0,X_1, \ldots, X_n$ una sequenza di punti appartenenti alla sezione locale e alla stessa traiettoria nell'ordine (cioè esistono $t_0< t_1 < t_2< \ldots <t_n$ tali che $X(t_j)=X_j$), allora lungo la sezione $g$ i punti $X_j$ formano una sequenza monotona, nel senso che se $g(s_j)=X_j, \;s_j\in I$, allora vale $s_0<s_1<s_2< \ldots <s_n$ oppure $s_0>s_1>s_2>\ldots >s_n$.

Dimostrazione del lemma:

L'arco di soluzione tra $X_0$ ed $X_1$, e l'arco di sezione locale tra $X_1$ ed $X_0$ formano una curva chiusa $C$, per cui (come illustrato dalla Figura 3.13) ci sono due soli casi: o la soluzione non può più uscire dall'interno $D$ di $C$ (Figura 3.13 a sinistra), e allora $X_2$ sta in $D$ e quindi `oltre' $X_1$ lungo $g$; oppure la soluzione non può entrare in $D$, e allora $X_2$ si trova fuori da $D$ e quindi `oltre' $X_1$ lungo $g$ (Figura 3.13 a destra).

C.D.D. lemma

Insiemi limite nel piano

Il lemma precedente, ed il teorema di invarianza degli insiemi limite, consentono di dimostrare il risultato principale della teoria qualitativa dei sistemi dinamici nel piano.

Nel piano ${\bf R}^2$ gli insiemi $\alpha$-limite ed $\omega$-limite non vuoti e compatti, che non contengono punti di equilibrio, sono orbite periodiche.
Dimostrazione (facoltativa):

Supponiamo che $L$ sia un insieme compatto e non vuoto, che sia $\omega$-limite di un'orbita $X(t)$, ma non contenga nessun punto di equilibrio. Sia $Y_0$ un punto di $L$, ed $Y(t)$ l'orbita con condizione iniziale $Y_0$: $L$ è compatto, quindi l'insieme $\omega$-limite di $Y(t)$ è non vuoto e contenuto in $L$. Sia $Z_0$ un punto nell'$\omega$-limite di $Y(t)$; poiché non è un punto di equilibrio, ha una sezione locale $g:I\to W$.

L'orbita $Y(t)$ deve avere una successione di punti $Y_k=Y(t_k)$ con $t_k\to +\infty$ e $Y_k\to Z_0$, per definizione di $\omega$-limite; ma allora a questa successione se ne può associare (almeno definitivamente, per $k$ abbastanza grande) un'altra $Y'_k=Y(t_k+\delta_k)$ che appartiene alla sezione locale e che tende a $Z_0$ lungo la sezione. Questo deriva dal fatto che la successione $Y_k$, avvicinandosi a $Z_0$, deve anche avvicinarsi alla sezione locale, e quindi entrare nell'intorno di quest'ultima a partire dal quale l'incontro con la sezione è inevitabile. La successione $Y'_k$ deve essere monotona sulla sezione locale $g$, per il lemma della sequenza monotona, e tendere a $Z_0$.

Prendiamo uno di questi punti $Y'_k$ sulla sezione locale per $Z_0$: poiché appartiene all'orbita per $Y_0$, è anche un punto dell'$\omega$-limite di $X(t)$ (gli insiemi $\omega$-limite sono invarianti). Applicando lo stesso ragionamento, anche sull'orbita $X(t)$ si trova una successione di punti $X'_{k,m}$ appartenenti alla sezione locale $g$, e che si avvicinano, al crescere di $m$, in modo monotono ad $Y'_k$.

Con da questa costruzione, si può completare la dimostrazione in quattro passi:

Passo 1: L'orbita per $Z_0$ incontra la sezione locale nel solo punto $Z_0$. Se così non fosse, una seconda intersezione $Z_1$ formerebbe con l'arco di orbita tra $Z_0$ e $Z_1$ e l'arco di sezione tra $Z_1$ e $Z_0$ una curva chiusa $C$; come nella Figura 3.13, si avrebbero due casi. Se $Z_1$ sta rispetto ad $Z_0$ sulla sezione dalla parte opposta rispetto agli $Y'_k$, l'orbita contenente $Z_0, Z_1$ entra nell'interno $D$ di $C$ e non può più uscirne, mentre l'orbita $Y(t)$ non può entrarvi. Ma allora vi sono dei punti sull'orbita per $Z_0$ che non possono essere punti limite dell'orbita $Y(t)$. Se invece $Z_1$ sta rispetto ad $Z_0$ sulla sezione dalla stessa parte degli $Y'_k$, i punti $Y'_k$ non possono avere $Z_0$ come limite.

Passo 2: L'orbita per $Y'_k$ incontra la stessa sezione locale nel solo punto $Y'_k$; il ragionamento è identico a quello del passo 1.

Passo 3: L'orbita per $Z_0$, contenuta nell'insieme $\omega$-limite dell'orbita $Y(t)$, incontra la sezione locale nel solo punto $Z_0$, mentre l'orbita stessa la incontra nel solo punto $Y'_k$. Questo è possibile solo se i due punti coincidono; altrimenti ci sarebbe una distanza minima $>0$ tra l'orbita $Y(t)$ e $Z_0$. Perciò $Y(t)$ è un'orbita periodica, perché non può ripassare arbitrariamente vicino a $Y'_k=Z_0$ senza passare dall'intorno della sezione locale a partire dal quale l'incontro con la sezione è inevitabile, e quindi deve ripassare esattamente dallo stesso punto.

Passo 4: L'insieme limite di $X(t)$ consiste solo della traiettoria $C$ dell'orbita periodica $Y(t)$. Per il teorema della curva di Jordan la traiettoria della soluzione $X(t)$ deve stare tutta o nell'interno $D$ o nell'esterno $E$ della curva $C$. Supponiamo che stia all'esterno: allora non può avere punti limite all'interno, perché $E\cup C$ è chiuso, ed i valori limite di qualsiasi successione di punti di un chiuso devono essere nel chiuso stesso. Perciò l'insieme limite $L$ non contiene punti di $D$. Se $P$ fosse un punto di $L\cap E$, esiste un intorno $U$ di $C$ che non contiene $P$. L'orbita $X(t)$ ha infiniti punti contenuti in $U$ che tendono ad un punto $V$ di $C$, in particolare ve ne sono che stanno su di una sezione locale passante per $V$. Per il lemma della sequenza monotona, si costruisce come in Figura 3.13 un insieme positivamente invariante che contiene $C$ ma sta in $U$, quindi non contiene $P$. Si ripete la stessa costruzione del passo 1, e si mostra che l'orbita $X(t)$ non può ripassare vicino a $P$. Se invece $X(t)$ sta all'interno, vale lo stesso ragionamento scambiando il ruolo di $D$ ed $E$.

 C.D.D.

Sia $C$ una curva chiusa che corrisponde ad una traiettoria di un sistema dinamico in ${\bf R}^2$, tale che l'insieme di definizione $W$ del sistema dinamico contiene l'intera regione che sta all'interno di $C$. Allora all'interno di $C$ esiste o almeno un punto di equilibrio o almeno un'altra orbita periodica (distinta da $C$).

Dimostrazione:

Si noti che il piano ${\bf R}^2$ è diviso dalla curva chiusa $C$ in tre parti disgiunte, cioè $C$ stessa, l'interno $D$ e l'esterno $E$, con $D$ ed $E$ due aperti (le componenti connesse di ${\bf R}^2-C$); questo è un caso (semplice, la curva essendo $C^1$) del teorema della curva di Jordan.

Poiché per ipotesi $D\subset W$, le soluzioni con condizioni iniziali in $D$ non possono uscire da $D$, altrimenti dovrebbero attraversare $C$ e questo contraddirebbe l'unicità della soluzione per il punto di incrocio. D'altro canto $D\cup C$ è chiuso e limitato, quindi compatto, e le soluzioni contenute in $D$ sono definite per ogni $t$ in ${\bf R}$, per il teorema di continuazione delle soluzioni. Perciò esse hanno insieme $\omega$-limite (anche $\alpha$-limite) non vuoto. L'insieme $\omega$-limite, oppure quello $\alpha$-limite, potrebbe essere $C$ (come in Figura 3.12); però $C$ non può essere contemporaneamente sia $\alpha$-limite che $\omega$-limite, senza contraddire il Lemma della sequenza monotona. Quindi, per il teorema di Poincaré-Bendixon, dentro $D$ deve esserci o un punto di equilibrio o un ciclo limite.

 C.D.D.

Se però dentro $D$ esistesse un ciclo limite $C_1$, questo racchiuderebbe un insieme invariante $D_1$, a cui si può applicare lo stesso ragionamento. A partire da questo argomento si potrebbe dimostrare che $D$ contiene in ogni caso un punto di equilibrio; per la dimostrazione si veda [Hirsch-Smale 74].

Problema Sia dato un sistema dinamico $\dot X = F(X)$ sulla corona circolare $W=\{1\leq x^2+y^2 \leq 2\}\subset {\bf R}^2$, con il campo vettoriale $F$ che non si annulla dentro e $W$ e sul bordo di $W$ punta ``dentro'' di $W$. Allora c'è almeno un'orbita periodica. (Soluzione)

Esercizio Sia $L$ l'insieme nel piano $(x,y)$ dei punti tali che

$$x^2+y^2=1 \ \ oppure \ \ \cases{x=0\cr \vert y\vert\leq 1} \ .$$

provare che $L$ non può essere l'insieme $\omega$-limite di un sistema dinamico. (Soluzione)

Insiemi limite più complessi

Il teorema di Poincaré-Bendixon non vale in dimensione $n>2$. Anche in dimensione 2, ma su superfici diverse dal piano, possono esistere insiemi limite che non contengono equilibri ma sono molto diversi da orbite periodiche.

Esempio:

Figura 3.14: Un sistema dinamico sul toro, definito dal passaggio al quoziente di un campo vettoriale costante sul piano.


Come esempio semplice di uno spazio diverso da ${\bf R}^n$, prendiamo un toro ${\bf T}^2$ definito come quoziente, ${\bf R}^2/(2\pi{\bf Z})^2$, ovvero come quadrato di lato $2\pi$ con i bordi identificati; le coordinate su ${\bf T}^2$ sono una coppia di variabili angolo $(\theta_1,\theta_2)$.

Come esempio di sistema dinamico continuo su ${\bf T}^2$ prendiamo un sistema dinamico costante su ${\bf R}^2$, cioè $\dot\theta_1=\nu_1\ ;\ \dot\theta_2=\nu_2$ e passiamolo al quoziente; si ottiene un sistema dinamico sul toro, il cui flusso integrale va sotto il nome di flusso di Kronecker. Se il rapporto $\nu_1/\nu_2$ è irrazionale, allora l'insieme $\omega$-limite di ogni orbita è tutto il toro; lo stesso per l'$\alpha$-limite. Se invece $\nu_1/\nu_2\in {\bf Q}$, tutte le orbite sono periodiche e quindi ciascuna coincide con i propri insieme limite.