Next: 5.5 TRASFORMAZIONI CANONICHE Up: 5. SISTEMI CONSERVATIVI Previous: 5.3 TRASFORMATA DI LEGENDRE Indice Indice analitico
Sommario Molti esempi di hamiltoniane che non sono del tipo semplice
![]() si ottengono per trasformata di Legendre a partire
dalle equazioni di Lagrange. I casi più notevoli sono quelli dei
moti vincolati, sia di corpi puntiformi, sia di corpi dotati di momento
d'inerzia non nullo (purché lo spazio delle configurazioni resti ad
una dimensione). La condizione che la funzione energia
potenziale sia di classe
si ottengono per trasformata di Legendre a partire
dalle equazioni di Lagrange. I casi più notevoli sono quelli dei
moti vincolati, sia di corpi puntiformi, sia di corpi dotati di momento
d'inerzia non nullo (purché lo spazio delle configurazioni resti ad
una dimensione). La condizione che la funzione energia
potenziale sia di classe ![]() può essere rilassata.
può essere rilassata.
Molti sistemi hamiltoniani non sono della forma che deriva da un
sistema newtoniano ad un grado di libertà. Per esempio, alcuni
sistemi hamiltoniani ad un grado di libertà possono essere ricavati
da sistemi newtoniani con più gradi di libertà in presenza di
vincoli. Il caso più importante è quello del moto vincolato
(a un grado di libertà) di un corpo puntiforme; con questo si
intende che un corpo puntiforme di massa ![]() si muova nello spazio
si muova nello spazio
![]() su di una curva
su di una curva ![]() con parametro
con parametro ![]() ; la curva si suppone
che sia regolare, di classe
; la curva si suppone
che sia regolare, di classe ![]() per
per
![]() . Allora l'energia cinetica del corpo
puntiforme sarà semplicemente
. Allora l'energia cinetica del corpo
puntiforme sarà semplicemente
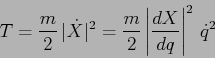
Non è facile dare una definizione fisica di corpo puntiforme, visto che si tratta di un'astrazione matematica. La definizione più chiara è questa: si tratta di un corpo per il quale l'energia cinetica è fornita solo dal movimento di un singolo punto rappresentativo (in pratica il suo centro di massa), ed è trascurabile qualsiasi contributo proveniente per esempio dall'energia cinetica dei moti di rotazione; quindi l'energia cinetica è data, per definizione, dalla formula precedente. La stessa formula dell'energia cinetica contiene anche la definizione matematica di massa, la cui definizione fisica è concettualmente più complicata, perché deve fare riferimento anche al principio di equivalenza.
Supponiamo che le forze esterne siano dotate di energia potenziale
![]() ; allora la funzione composta, in sostanza la restrizione
dell'energia potenziale alla curva,
; allora la funzione composta, in sostanza la restrizione
dell'energia potenziale alla curva, ![]() , avrà come
derivata rispetto a
, avrà come
derivata rispetto a ![]()
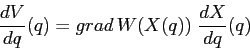
Se facciamo l'ipotesi che le componenti delle forze normali alla curva
siano annullate dalle reazioni vincolari, che appunto forzano il
moto a restare confinato alla curva, ma hanno componente nulla lungo
la tangente alla curva, allora l'equazione di moto lungo la curva
sarà esprimibile mediante la lagrangiana
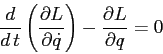
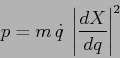
![\begin{eqnarray*}
\frac d{d\,t}\left(\frac{\partial {L}}{\partial {\dot q}}\righ...
...} =
\left[m\ddot X + \nabla W\right]\cdot \frac{d{X}}{d{q}}=0\;.
\end{eqnarray*}](img1705.png)
Quindi l'equazione di Lagrange esprime il fatto che l'accelerazione
![]() subita dal corpo puntiforme è compensata dalla forza
esterna di potenziale
subita dal corpo puntiforme è compensata dalla forza
esterna di potenziale ![]() soltanto per la componente nella direzione
tangente alla curva di vincolo. L'equazione di Lagrange non contiene
informazioni sulla componente normale alla curva delle equazioni di
Newton. Le equazioni di Newton contengono un altro termine che esprime
le reazioni vincolari
soltanto per la componente nella direzione
tangente alla curva di vincolo. L'equazione di Lagrange non contiene
informazioni sulla componente normale alla curva delle equazioni di
Newton. Le equazioni di Newton contengono un altro termine che esprime
le reazioni vincolari ![]() , cioè delle forze esercitate dal vincolo
sul corpo in movimento per mantenerlo sul vincolo stesso:
, cioè delle forze esercitate dal vincolo
sul corpo in movimento per mantenerlo sul vincolo stesso:
Il moto vincolato può essere generalizzato al caso di più punti
materiali, per esempio due punti ![]() in
in ![]() con masse
con masse
![]() . Supponiamo che ci siano dei vincoli tali che i moti di
tutti e due i punti siano parametrizzati da una sola coordinata
. Supponiamo che ci siano dei vincoli tali che i moti di
tutti e due i punti siano parametrizzati da una sola coordinata ![]() ,
cioè
,
cioè ![]() e
e ![]() , allora l'energia cinetica si esprime come
, allora l'energia cinetica si esprime come
Esercizio
Un corpo puntiforme di massa ![]() viene lanciato verso l'alto, in
direzione perfettamente verticale, sotto l'attrazione della
gravità terrestre con energia potenziale (in funzione della
coordinata verticale
viene lanciato verso l'alto, in
direzione perfettamente verticale, sotto l'attrazione della
gravità terrestre con energia potenziale (in funzione della
coordinata verticale ![]() ):
):
Esercizio
Dato un corpo puntiforme di massa ![]() vincolato
all'elica cilindrica
vincolato
all'elica cilindrica
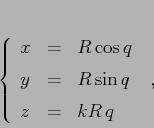
Prendiamo un corpo puntiforme di massa ![]() che si muove nel piano
che si muove nel piano
![]() vincolato alla curva
vincolato alla curva
![]() , sotto l'azione di un
campo di forze con energia potenziale
, sotto l'azione di un
campo di forze con energia potenziale ![]() , per esempio per
effetto di un campo di gravità costante rivolto in direzione
dell'asse
, per esempio per
effetto di un campo di gravità costante rivolto in direzione
dell'asse ![]() negativo, e di intensità costante
negativo, e di intensità costante ![]() . Si noti che
l'energia potenziale è proporzionale alla stessa costante
. Si noti che
l'energia potenziale è proporzionale alla stessa costante ![]() , il
che introduce un'altra delle proprietà fondamentali della
massa, il principio di equivalenza per cui massa
inerziale e massa gravitazionale sono esattamente proporzionali.
Comunque ai fini delle equazioni di moto non ha importanza quale è
la causa fisica della forza. Il corrispondente sistema dinamico -
sia esso espresso con l'equazione di Lagrange oppure con le
equazioni di Hamilton - è il pendolo (nonlineare
conservativo).
, il
che introduce un'altra delle proprietà fondamentali della
massa, il principio di equivalenza per cui massa
inerziale e massa gravitazionale sono esattamente proporzionali.
Comunque ai fini delle equazioni di moto non ha importanza quale è
la causa fisica della forza. Il corrispondente sistema dinamico -
sia esso espresso con l'equazione di Lagrange oppure con le
equazioni di Hamilton - è il pendolo (nonlineare
conservativo).
Se parametrizziamo la circonferenza del vincolo con l'angolo ![]() misurato a partire dal ``basso'' (cioè dall'asse
misurato a partire dal ``basso'' (cioè dall'asse ![]() negativo), allora
negativo), allora
![\begin{displaymath}
X(\theta)=\left[\begin{array}{c}{x(\theta)}\\
{y(\theta)}...
...}{\ell\,\sin\theta}\\
{-\ell\,\cos\theta}\end{array}\right]
\end{displaymath}](img1725.png)
![\begin{displaymath}
L(\theta,\dot \theta)=T(\theta,\dot \theta)-V(\theta)=\frac...
...}{d{\theta}}\right)^2\right] \, \dot \theta^2 - mg\,y(\theta)
\end{displaymath}](img1726.png)
La costante ![]() moltiplica la lagrangiana che si
potrebbe dividere per
moltiplica la lagrangiana che si
potrebbe dividere per ![]() senza che l'equazione di Lagrange,
che contiene solo derivate, cambi.
senza che l'equazione di Lagrange,
che contiene solo derivate, cambi.
Il momento è quindi
Il sistema può anche essere ridotto alla forma newtoniana
dividendo la lagrangiana per ![]() (e quindi ponendo
(e quindi ponendo
![]() , il momento uguale alla
velocità angolare),
e in questa forma è già stato
studiato nella Sezione 3.4.
, il momento uguale alla
velocità angolare),
e in questa forma è già stato
studiato nella Sezione 3.4.
Il fatto che lo spazio delle configurazioni, cioè l'insieme
in cui può muoversi il vettore di stato ![]() , sia una
circonferenza rende possibile spiegare in modo razionale la natura
della coordinata lagrangiana
, sia una
circonferenza rende possibile spiegare in modo razionale la natura
della coordinata lagrangiana
![]() . In effetti il punto materiale appartiene ad una
circonferenza
. In effetti il punto materiale appartiene ad una
circonferenza ![]() , che è una curva regolare;
, che è una curva regolare; ![]() è una
variabile reale che viene impiegata come parametrizzazione di
è una
variabile reale che viene impiegata come parametrizzazione di
![]() . Allora la definizione di una variabile angolo è
quella della parametrizzazione, cioè un'applicazione
. Allora la definizione di una variabile angolo è
quella della parametrizzazione, cioè un'applicazione
![]() ; con il simbolo
; con il simbolo ![]() si indicano
ambiguamente sia la variabile indipendente che il punto
parametrizzato sulla curva, e quindi si può considerare sia
si indicano
ambiguamente sia la variabile indipendente che il punto
parametrizzato sulla curva, e quindi si può considerare sia
![]() che
che ![]() , ma di volta in volta bisogna
specificare chiaramente cosa si intende.
, ma di volta in volta bisogna
specificare chiaramente cosa si intende.
Possiamo usare il pendolo ordinario anche come esempio di un calcolo
esplicito delle reazioni vincolari: basta calcolare la violazione
delle equazioni di Newton che si ottiene assumendo che non ci siano
reazioni vincolari.
![\begin{displaymath}
\frac{d{X}}{d{t}} = \ell\,\dot\theta\; \left[\begin{array}{...
...bla W= \left[\begin{array}{c}{0}\\
{m\,g}\end{array}\right]
\end{displaymath}](img1739.png)
![\begin{displaymath}
m\,\frac{d^2{X}}{d{t}^2}+\nabla W = m\; \left[\begin{array}...
... + \ell\,\cos\theta\,{\dot\theta}^2+ g}\end{array}\right] \ ,
\end{displaymath}](img1740.png)
![\begin{displaymath}
m\,\frac{d^2{X}}{d{t}^2}+\nabla W = m\; \left[\begin{array}...
...+ \ell\,\cos\theta\,{\dot\theta}^2+ g}\end{array}\right]=R\ .
\end{displaymath}](img1742.png)
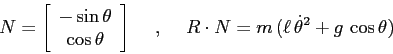
Esercizio
Fissando una delle estremità di un filo inestendibile di lunghezza
![]() ad un punto materiale di massa
ad un punto materiale di massa ![]() , e l'altra estremità al
punto più alto di una guida circolare di raggio
, e l'altra estremità al
punto più alto di una guida circolare di raggio ![]() (cfr. Figura 5.5), lo si lasci oscillare sotto l'azione
di una forza di gravità di intensità
(cfr. Figura 5.5), lo si lasci oscillare sotto l'azione
di una forza di gravità di intensità ![]() rivolta verso il basso.
rivolta verso il basso.
Studiare il moto del pendolo sul piano verticale della guida e determinare la frequenza delle piccole oscillazioni intorno al punto di equilibrio stabile.
Suggerimento: Come coordinata, servirsi di
![]() , dove
, dove ![]() è
l'angolo formato dalla direzione del filo con la verticale.
è
l'angolo formato dalla direzione del filo con la verticale.
Esempio:
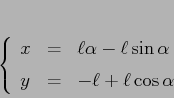
 |
Si noti che ![]() non è una variabile angolo, perché la
parametrizzazione della curva non è periodica. Il moto è quello
di un punto su di una ruota che, senza strisciare, rotola
lungo il soffitto.
non è una variabile angolo, perché la
parametrizzazione della curva non è periodica. Il moto è quello
di un punto su di una ruota che, senza strisciare, rotola
lungo il soffitto.
Le equazioni di Lagrange nella variabile ![]() sono complicate,
ma è possibile semplificarle usando il teorema di
covarianza dell'equazione di Lagrange. In particolare in
questo caso conviene usare un parametro arco
sono complicate,
ma è possibile semplificarle usando il teorema di
covarianza dell'equazione di Lagrange. In particolare in
questo caso conviene usare un parametro arco
![]() , il quale è definito dalla condizione che il vettore
velocità della curva rispetto ad
, il quale è definito dalla condizione che il vettore
velocità della curva rispetto ad ![]() sia di lunghezza 1; come è
noto il parametro arco ha la proprietà di misurare la
lunghezza della curva, cioè l'incremento di
sia di lunghezza 1; come è
noto il parametro arco ha la proprietà di misurare la
lunghezza della curva, cioè l'incremento di ![]() su di un
tratto di curva è la sua lunghezza. Per determinare
su di un
tratto di curva è la sua lunghezza. Per determinare ![]() si usa la
condizione
si usa la
condizione
![\begin{displaymath}
1=\left(\frac{d{x}}{d{s}} \right)^2+\left(\frac{d{y}}{d{s}}...
...pha}}\right)^2\right]\; \left(\frac{d{\alpha}}{d{s}}\right)^2
\end{displaymath}](img1752.png)
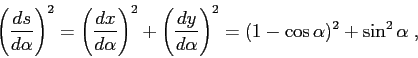
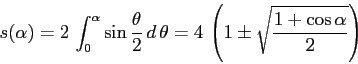
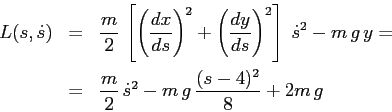
Ne segue che il pendolo cicloidale è perfettamente isocrono, non
solo approssimativamente per le piccole oscillazioni. Si badi però
che la parametrizzazione cessa di essere regolare per ![]() ed
ed ![]() , ossia per
, ossia per ![]() ; quindi anche le equazioni di
Lagrange non sono valide per oscillazioni più ampie. Il pendolo
cicloidale ha le stesse equazioni di moto del pendolo lineare, ma
solo per oscillazioni di ampiezza non superiore a
; quindi anche le equazioni di
Lagrange non sono valide per oscillazioni più ampie. Il pendolo
cicloidale ha le stesse equazioni di moto del pendolo lineare, ma
solo per oscillazioni di ampiezza non superiore a ![]() .
.
Se un corpo puntiforme è vincolato a muoversi nel piano ![]() lungo il grafico
lungo il grafico ![]() di una funzione
di una funzione ![]() , allora l'energia
cinetica si calcola usando la parametrizzazione
, allora l'energia
cinetica si calcola usando la parametrizzazione ![]() :
:
Se facciamo la solita assunzione del campo di forze di intensità
![]() rivolte verso le
rivolte verso le ![]() negative, si ottiene
negative, si ottiene
La corrispondente hamiltoniana si calcola con la
trasformata di Legendre inversa:
![\begin{displaymath}
H(p,x)=\frac{p^2}{2m\,\left[1+\left(f'(x)\right)^2\right]} + m\,g\,f(x)\;.
\end{displaymath}](img1777.png)
Se invece si usa come parametro sulla curva ![]() il parametro
arco
il parametro
arco ![]() , allora
, allora
![]() dove
dove ![]() è la parametrizzazione della
è la parametrizzazione della ![]() mediante
mediante ![]() . Però non è
detto che sia semplice calcolare esplicitamente l'integrale che
definisce
. Però non è
detto che sia semplice calcolare esplicitamente l'integrale che
definisce ![]() e poi invertire trovando un'espressione esplicita
di
e poi invertire trovando un'espressione esplicita
di ![]() , salvo che per funzioni
, salvo che per funzioni ![]() molto particolari.
molto particolari.
Esercizio
Studiare il moto di corpi puntiformi, su cui agisce una forza verso
le ![]() negative e di intensità costante
negative e di intensità costante ![]() , vincolati al
grafico
, vincolati al
grafico ![]() .
.
Se un corpo non è puntiforme, per
definizione la sua energia cinetica non si riduce alla sola energia
cinetica di traslazione. Supponiamo che il corpo sia libero di ruotare
soltanto attorno ad un asse con direzione fissa, e sia ![]() l'angolo di rotazione: allora l'energia cinetica di rotazione sarà
della forma
l'angolo di rotazione: allora l'energia cinetica di rotazione sarà
della forma
![]() , dove il coefficiente
, dove il coefficiente ![]() è il
momento d'inerzia rispetto all'unico asse di rotazione.
è il
momento d'inerzia rispetto all'unico asse di rotazione.
Per esempio, per un cilindro di raggio ![]() e massa
e massa ![]() che ruota
attorno all'asse di simmetria, se la densità è uniforme il momento
d'inerzia è
che ruota
attorno all'asse di simmetria, se la densità è uniforme il momento
d'inerzia è ![]() . Per una sfera di densità uniforme
. Per una sfera di densità uniforme
![]() . In generale il momento d'inerzia sarà sempre della
forma
. In generale il momento d'inerzia sarà sempre della
forma ![]() se
se ![]() è la massa del corpo ed
è la massa del corpo ed ![]() una
lunghezza caratteristica della sua forma, dove il coefficiente
una
lunghezza caratteristica della sua forma, dove il coefficiente
![]() dipende sia dalla forma che dalla distribuzione interna di
massa.
dipende sia dalla forma che dalla distribuzione interna di
massa.
Esempio:
Allora l'energia cinetica, somma di quella di traslazione di un
corpo puntiforme con la stessa massa della pallina e di quella di
rotazione, è:
L'esperimento di Galileo è quindi un esperimento sui moti
uniformemente accelerati, ma graduando l'angolo di pendenza ![]() si possono ottenere accelerazioni molto minori di
si possono ottenere accelerazioni molto minori di ![]() ; questo era lo
scopo di Galileo nell'usare il piano inclinato, vista la
difficoltà di misurare accuratamente i tempi. Si noti che il
limite per
; questo era lo
scopo di Galileo nell'usare il piano inclinato, vista la
difficoltà di misurare accuratamente i tempi. Si noti che il
limite per ![]() non è possibile, perché la velocità alla
periferia del corpo rotante tenderebbe all'infinito; in effetti
l'approssimazione del corpo puntiforme conduce ad un risultato
diverso.
non è possibile, perché la velocità alla
periferia del corpo rotante tenderebbe all'infinito; in effetti
l'approssimazione del corpo puntiforme conduce ad un risultato
diverso.
Esercizio
Supponiamo che la distribuzione interna di massa del corpo che rotola
lungo un piano inclinato, come nell'esperimento di Galileo,
sia non uniforme. Come esempio estremo supponiamo che tutta la massa
di un cilindro rotolante su di un piano inclinato di un angolo
![]() sia concentrata in un corpo puntiforme di massa
sia concentrata in un corpo puntiforme di massa ![]() fissato
ad una distanza
fissato
ad una distanza ![]() dall'asse del cilindro. Supponiamo che il
corpo puntiforme sia soggetto alla forza di gravità di intensità
dall'asse del cilindro. Supponiamo che il
corpo puntiforme sia soggetto alla forza di gravità di intensità
![]() lungo la verticale. Trovare le equazioni di Lagrange e di
Hamilton, determinare per quali valori dei parametri
lungo la verticale. Trovare le equazioni di Lagrange e di
Hamilton, determinare per quali valori dei parametri
![]() ci sono dei punti di equlibrio, e discuterne la stabilità.
ci sono dei punti di equlibrio, e discuterne la stabilità.
Suggerimento: Parametrizzare la traiettoria del corpo puntiforme con
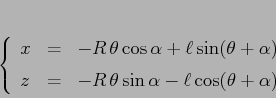
Il formalismo lagrangiano si può utilizzare anche per sistemi nei quali non vale la conservazione dell'energia. Questo si verifica nei sistemi rotanti, in cui si suppone che la rotazione di una o più masse venga mantenuta da un ``motore'' esterno al sistema. Il sistema non essendo isolato, non c'è conservazione dell'energia, ma la funzione energia ha una derivata totale non nulla che rappresenta la potenza consumata dal motore che mantiene la rotazione.
Supponiamo che la rotazione avvenga attorno all'asse ![]() , cioè su di
una superficie di rotazione di equazioni
, cioè su di
una superficie di rotazione di equazioni
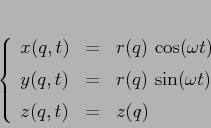
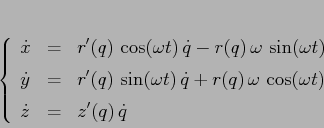
Il sistema così ottenuto è comunque integrabile: infatti la
trasformazione di Legendre e la sua inversa
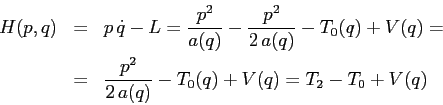
Si può verificare che la potenza richiesta al motore esterno
che mantiene la rotazione altro non è che
![]() dove
dove
![]() è il momento di inerzia del corpo puntiforme rispetto
all'asse fisso di rotazione.
è il momento di inerzia del corpo puntiforme rispetto
all'asse fisso di rotazione.
Un punto di vista alternativo è quello di considerare un vincolo
piano nel sistema rotante, usando le coordinate ![]() . La
lagrangiana come funzione di
. La
lagrangiana come funzione di ![]() resta la stessa, ma
l'energia cinetica è solo
resta la stessa, ma
l'energia cinetica è solo ![]() e il termine
e il termine ![]() della hamiltoniana
della hamiltoniana ![]() si interpreta come energia potenziale
si interpreta come energia potenziale
![]() associata alla forza centrifuga di intensità
associata alla forza centrifuga di intensità ![]() .
.
Esercizio
Consideriamo il toro ottenuto come figura di rotazione, cioè
facciamo ruotare la circonferenza
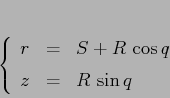
Esempio:
![\begin{displaymath}
H(p,r)= \frac {p^2}{2\,m\; \left\{ 1 + \left[f'(r)\right]^2 \right\}}
- \frac m2 \, \omega^2\, r^2 + m\,g\, f(r)
\end{displaymath}](img1839.png)
![\begin{displaymath}
\dot q= \frac{\partial {H}}{\partial {p}} = \frac p{m\; \left\{ 1 + \left[f'(r)\right]^2 \right\}}=0
\end{displaymath}](img1840.png)
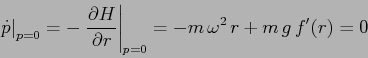
Esercizio
Supponiamo che la curva ruotante con velocità angolare costante
![]() nel piano verticale sia
nel piano verticale sia ![]() , la massa
, la massa ![]() e l'energia
potenziale
e l'energia
potenziale ![]() . Per quali valori dei parametri
. Per quali valori dei parametri ![]() il punto di equilibrio
il punto di equilibrio ![]() è stabile?
(Soluzione)
è stabile?
(Soluzione)
Esercizio
Supponiamo che la curva ruotante con velocità angolare costante
![]() nel piano verticale sia
nel piano verticale sia ![]() (come le rigature di un
vecchio disco). Al disco sia appoggiato un corpo puntiforme di massa
(come le rigature di un
vecchio disco). Al disco sia appoggiato un corpo puntiforme di massa
![]() con l'energia potenziale
con l'energia potenziale ![]() . Scrivere l'equazione di
Lagrange e le equazioni di Hamilton.
Descrivere i punti di equilibrio stabili e instabili del sistema. Si
provi in particolare che per
. Scrivere l'equazione di
Lagrange e le equazioni di Hamilton.
Descrivere i punti di equilibrio stabili e instabili del sistema. Si
provi in particolare che per ![]() abbastanza grande, per
esempio per
abbastanza grande, per
esempio per
![]() , non ci sono punti di equilibrio.
(Soluzione)
, non ci sono punti di equilibrio.
(Soluzione)
Si consideri un sistema hamiltoniano ad un grado di libertà con
coordinata ![]() . Sia
. Sia ![]() un parametro reale al variare del quale può
cambiare il numero dei punti di equilibrio. Il diagramma di
biforcazione è un grafico nel piano
un parametro reale al variare del quale può
cambiare il numero dei punti di equilibrio. Il diagramma di
biforcazione è un grafico nel piano ![]() che rappresenta il
valore delle configurazioni di equilibrio in corrispondenza a
che rappresenta il
valore delle configurazioni di equilibrio in corrispondenza a ![]() .
Possiamo indicare anche la stabilità di tali configurazioni
adottando per esempio la convenzione di usare una curva continua per
l'
.
Possiamo indicare anche la stabilità di tali configurazioni
adottando per esempio la convenzione di usare una curva continua per
l'![]() -mo equilibrio
-mo equilibrio ![]() negli intervalli in cui questo è
stabile ed una curva tratteggiata quando è instabile.
negli intervalli in cui questo è
stabile ed una curva tratteggiata quando è instabile.
Esempio:
Nel sistema di riferimento ruotante l'energia cinetica e potenziale,
in funzione di ![]() , sono rispettivamente
, sono rispettivamente
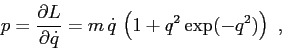
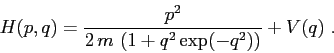

La condizione che la funzione di Hamilton, e quella di Lagrange, siano
di classe ![]() , è conveniente ma non è indispensabile. Il teorema
di esistenza e unicità richiede
che il secondo membro di un sistema dinamico sia una funzione
lipschitziana, quindi continua ma non necessariamente
differenziabile. Per esempio, in un sistema hamiltoniano (proveniente
da uno newtoniano)
, è conveniente ma non è indispensabile. Il teorema
di esistenza e unicità richiede
che il secondo membro di un sistema dinamico sia una funzione
lipschitziana, quindi continua ma non necessariamente
differenziabile. Per esempio, in un sistema hamiltoniano (proveniente
da uno newtoniano)
![]() , supponiamo che
, supponiamo che ![]() sia
sia
![]() ovunque salvo che in un numero finito di punti, nei quali
ammette derivata destra e sinistra. La funzione
ovunque salvo che in un numero finito di punti, nei quali
ammette derivata destra e sinistra. La funzione ![]() risulta
comunque localmente lipschitziana, e l'esistenza e unicità della
soluzione sono assicurate anche quando essa passa da questi punti
singolari.
risulta
comunque localmente lipschitziana, e l'esistenza e unicità della
soluzione sono assicurate anche quando essa passa da questi punti
singolari.
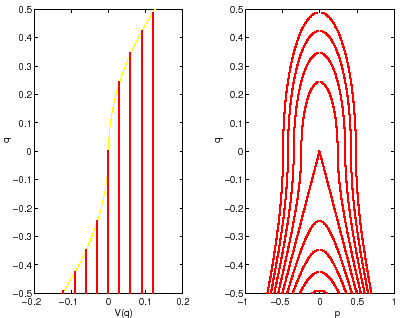 |
Esempio: