Next: 4.2 METODO DI EULERO Up: 4. DISCRETIZZAZIONE Previous: 4. DISCRETIZZAZIONE Indice Indice analitico
Sommario Un sistema alle differenze finite lineari si risolve
calcolando le potenze di una matrice; questo calcolo diventa molto
più semplice se la matrice è ridotta alla forma canonica di
Jordan. Modelli alle differenze finite lineari sono impiegati in molti
campi; qui diamo degli esempi tratti dalla modellizzazione di fenomeni
economici.
Un sistema dinamico discreto lineare in ![]() è
della forma:
è
della forma:
Si può
allora cercare di semplificare questo calcolo mediante un
cambiamento di coordinate lineare: se
![]() è la stessa orbita vista in un nuovo sistema di coordinate,
associate alla base
è la stessa orbita vista in un nuovo sistema di coordinate,
associate alla base
![]() mediante la matrice
mediante la matrice ![]() con
colonne
con
colonne ![]() (si ricorda che in tal caso
(si ricorda che in tal caso ![]() è invertibile, e
è invertibile, e
![]() ), allora
), allora
Quindi nel nuovo sistema di coordinate ![]() il sistema dinamico
discreto ha per matrice
il sistema dinamico
discreto ha per matrice
![]() e per soluzione
e per soluzione
![]() ; se la nuova base è scelta in modo che il calcolo
delle potenze di
; se la nuova base è scelta in modo che il calcolo
delle potenze di ![]() sia più semplice, allora converrà esprimere
la soluzione passando attraverso
sia più semplice, allora converrà esprimere
la soluzione passando attraverso ![]() , cioè:
, cioè:
L'analogia con il caso continuo è così stretta che non vale la pena di ripetere la discussione dei vari casi di autovalori coniugati, di una matrice semisemplice e con parte nilpotente; si può passare direttamente al risultato generale, utilizzando la forma canonica di Jordan.
Per il teorema della decomposizione S + N la matrice ![]() può comunque essere descritta come somma di una matrice semisemplice
può comunque essere descritta come somma di una matrice semisemplice ![]() ed una matrice nilpotente
ed una matrice nilpotente ![]() , che commutano tra loro:
, che commutano tra loro: ![]() .
Allora vale la formula del binomio di Newton:
.
Allora vale la formula del binomio di Newton:
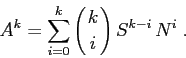
Per ogni matrice ![]() di tipo
di tipo ![]() , le soluzioni di
, le soluzioni di
![]() hanno componenti che si possono esprimere come
combinazioni lineari delle seguenti successioni:
hanno componenti che si possono esprimere come
combinazioni lineari delle seguenti successioni:
Si noti che i
coefficienti del polinomio ![]() dipendono da
dipendono da ![]() . Se si
vuole esprimere la dipendenza da
. Se si
vuole esprimere la dipendenza da ![]() , e non da
, e non da
![]() , si può usare l'espressione
, si può usare l'espressione
![]() dove
dove ![]() è
un polinomio di grado
è
un polinomio di grado ![]() che contiene monomi di grado
che contiene monomi di grado
![]() .
.
Dimostrazione:
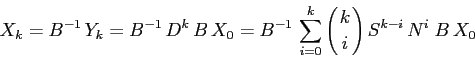
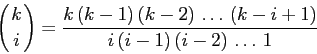
Definizione:
Si dice che
![]() è una
mappa asintoticamente stabile
nel punto
è una
mappa asintoticamente stabile
nel punto ![]() se è stabile, ed inoltre
esiste un intorno
se è stabile, ed inoltre
esiste un intorno ![]() di
di ![]() tale che
tale che
Supponiamo che
![]() sia un'applicazione lineare,
cioè
sia un'applicazione lineare,
cioè ![]() con
con ![]() una matrice
una matrice ![]() .
Poiché le successioni
.
Poiché le successioni ![]() contengono le potenze
contengono le potenze ![]() -esime degli
autovalori, la stabilità della soluzione nulla
-esime degli
autovalori, la stabilità della soluzione nulla
![]() è controllata dai moltiplicatori di Lyapounov, che sono i
moduli degli autovalori: l'applicazione lineare è asintoticamente
stabile nel punto
è controllata dai moltiplicatori di Lyapounov, che sono i
moduli degli autovalori: l'applicazione lineare è asintoticamente
stabile nel punto
![]() se e solo se tutti i
moltiplicatori di Lyapounov sono minori di
se e solo se tutti i
moltiplicatori di Lyapounov sono minori di ![]() .
.
Avere tutti i moltiplicatori di Lyapounov ![]() è
necessario, ma non sufficiente per la stabilità della soluzione
nulla; infatti in presenza di autovalori multipli di modulo
è
necessario, ma non sufficiente per la stabilità della soluzione
nulla; infatti in presenza di autovalori multipli di modulo ![]() possono essere presenti termini a crescenza polinomiale nell'indice
possono essere presenti termini a crescenza polinomiale nell'indice ![]() .
.
L'analogia con il teorema del pozzo lineare può essere
resa esplicita definendo, in questo caso, gli
esponenti di Lyapounov
come i logaritmi naturali dei moltiplicatori di Lyapounov,
cioè come i numeri reali ![]() per ogni autovalore
per ogni autovalore ![]() della matrice
della matrice ![]() del sistema dinamico discreto lineare.
del sistema dinamico discreto lineare.
Questa seconda definizione di esponenti di Lyapounov è
coerente con la precedente, nel senso che segue. Se ![]() è un
sistema dinamico continuo lineare, ed i suoi esponenti di Lyapounov
sono
è un
sistema dinamico continuo lineare, ed i suoi esponenti di Lyapounov
sono ![]() , con
, con
![]() , consideriamo il
sistema dinamico discreto lineare ottenuto per
discretizzazione con passo
, consideriamo il
sistema dinamico discreto lineare ottenuto per
discretizzazione con passo ![]() :
:
Vale anche il risultato analogo dei teoremi del pozzo nonlineare e della sorgente nonlineare:
Sia
![]() un sistema dinamico discreto,
un sistema dinamico discreto, ![]() un
punto fisso, tale che
un
punto fisso, tale che ![]() , e
, e ![]() la matrice jacobiana
di
la matrice jacobiana
di ![]() in
in ![]() . Se tutti i moltiplicatori di Lyapounov di
. Se tutti i moltiplicatori di Lyapounov di ![]() sono
minori di 1, allora
sono
minori di 1, allora ![]() è asintoticamente stabile in
è asintoticamente stabile in ![]() ; se tutti
i moltiplicatori di Lyapounov sono maggiori di 1,
; se tutti
i moltiplicatori di Lyapounov sono maggiori di 1, ![]() è
asintoticamente stabile in
è
asintoticamente stabile in ![]() .
.
Dimostrazione omessa.
In generale, una successione può essere definita per ricorrenza da
una funzione di un certo numero di valori precedenti; per esempio si
parla di equazione alle differenze finite di
ordine 2 quando
![\begin{displaymath}
V_k=\left[\begin{array}{c}{X_{k+1}}\\
{X_k}\end{array}\right]
\end{displaymath}](img1204.png)
![\begin{displaymath}
\left[\begin{array}{c}{X_{k+2}}\\
{X_{k+1}}\end{array}\rig...
...{array}{c}{F(X_{k+1},X_k)}\\
{X_{k+1}}\end{array}\right] \ .
\end{displaymath}](img1205.png)
Esempio:
![\begin{displaymath}
\left[\begin{array}{c}{x_{k+2}}\\
{x_{k+1}}\end{array}\rig...
...,\left[\begin{array}{c}{x_{k+1}}\\
{x_{k}}\end{array}\right]
\end{displaymath}](img1207.png)
![\begin{displaymath}
\left[\begin{array}{c}{x_{k+1}}\\
{x_k}\end{array}\right]=A^k\, \left[\begin{array}{c}{x_1}\\
{x_0}\end{array}\right]
\end{displaymath}](img1210.png)
Esercizio Studiare i seguenti problemi alle differenze finite lineari del secondo ordine:
![\begin{displaymath}\left\{\begin{array}{l}
{\displaystyle x_{k+2}=x_{k+1}+x_k}\\ [2mm]
{\displaystyle x_0=1\;,\;x_1=1}
\end{array}\right.\;;
\end{displaymath}](img1211.png)
![\begin{displaymath}\left\{\begin{array}{l}
{\displaystyle x_{k+2}=2x_{k+1}-4x_k}\\ [2mm]
{\displaystyle x_0=0\;,\;x_1=1}
\end{array}\right.\;?
\end{displaymath}](img1213.png)
Diamo di seguito alcuni esempi di modelli di fenomeni economici mediante equazioni alle differenze finite lineari. Gli esempi citati sono microeconomici, cioè descrivono la legge della domanda e dell'offerta per un singolo bene su di un dato mercato; esistono però anche modelli alle differenze finite di fenomeni macroeconomici, cioè dell'andamento di un intera economia.
Esempio:
Il modello della ragnatela dell'equilibrio di un mercato è un
sistema dinamico discreto lineare in ![]() , con tre variabili
, con tre variabili
![]() la cui interpretazione è la seguente:
la cui interpretazione è la seguente:
Il tempo è discreto, ![]() (come è logico perché i fenomeni
economici non possono essere istantanei).
(come è logico perché i fenomeni
economici non possono essere istantanei).
Le equazioni del modello sono le seguenti:
 |
Si può comprendere dall'equazione (2) che l'unità di tempo corrisponde al tempo necessario per la produzione; per esempio può essere un anno per i prodotti agricoli che possono essere seminati e raccolti solo una volta all'anno.
Allora si può ricavare una singola equazione alle differenze finite per
la variabile ![]() che rappresenta il prezzo:
che rappresenta il prezzo:
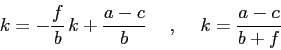
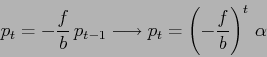
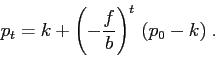
Qualitativamente la soluzione è un'oscillazione (![]() ) che è
smorzata se
) che è
smorzata se ![]() , amplificata se
, amplificata se ![]() ; nel primo caso la
soluzione tende a
; nel primo caso la
soluzione tende a
![]() per
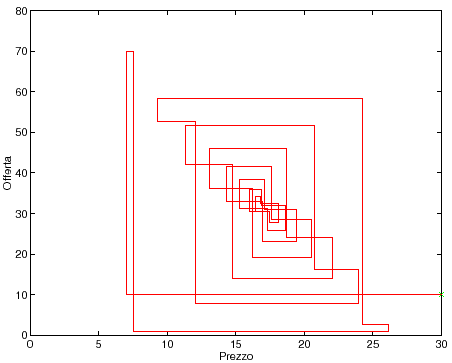
per ![]() , seguendo un
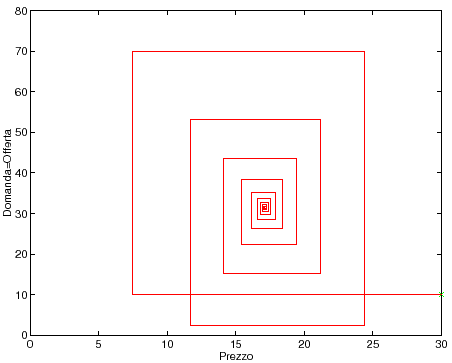
percorso che ha l'aspetto di una ragnatela (se si congiunge ogni punto
dell'orbita con il successivo mediante due segmenti paralleli agli
assi, vedi Figura 4.1).
, seguendo un
percorso che ha l'aspetto di una ragnatela (se si congiunge ogni punto
dell'orbita con il successivo mediante due segmenti paralleli agli
assi, vedi Figura 4.1).
Esempio:
Il modello delle scorte si ottiene modificando, nel modello
della ragnatela, l'equazione di equilibrio di mercato,
assumendo che domanda ed offerta possano non essere in equilibrio e
generare delle scorte ![]() ; allora l'equazione (3) è rimpiazzata
da:
; allora l'equazione (3) è rimpiazzata
da:
 |
Possiamo sintetizzare le equazioni (1), (2), (4) e (5) in un'unica equazione
alle differenze finite di ordine 2 per la variabile prezzo:
![\begin{displaymath}
\left[\begin{array}{c}{p_{t+1}}\\
{p_t}\end{array}\right]=...
...\; \left[\begin{array}{c}{p_t}\\
{p_{t-1}}\end{array}\right]
\end{displaymath}](img1248.png)
Andrea Milani 2009-06-01