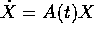 , in
cui la matrice
, in
cui la matrice 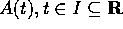 dei coefficienti dipende dal
tempo, le soluzioni esistono ancora per ogni condizione iniziale, e
sono tutte definite sull'intervallo I, per il teorema di
esistenza (caso lineare) .
dei coefficienti dipende dal
tempo, le soluzioni esistono ancora per ogni condizione iniziale, e
sono tutte definite sull'intervallo I, per il teorema di
esistenza (caso lineare) .
Sommario Per un sistema lineare non autonomo le soluzioni esistono per ogni valore della variabile indipendente per cui sono definiti e e continui i secondi membri. Si possono trarre conclusioni sulla stabilità dell'origine studiando l'evoluzione di un parallelepipedo intorno all'origine: se il volume tende a zero nel tempo, l'origine sarà un pozzo. Il volume evolve secondo un'equazione differenziale lineare in dimensione 1, in cui compare la traccia della matrice dei coefficienti del secondo membro.
Il comportamento qualitativo delle soluzioni può essere studiato per mezzo del legame fra gli invarianti del flusso integrale e gli invarianti della matrice A(t).
Nel caso di un sistema lineare non autonomo 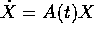 , in
cui la matrice
, in
cui la matrice 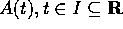 dei coefficienti dipende dal
tempo, le soluzioni esistono ancora per ogni condizione iniziale, e
sono tutte definite sull'intervallo I, per il teorema di
esistenza (caso lineare) .
dei coefficienti dipende dal
tempo, le soluzioni esistono ancora per ogni condizione iniziale, e
sono tutte definite sull'intervallo I, per il teorema di
esistenza (caso lineare) .
Definizione:
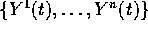 il determinante della loro matrice:
il determinante della loro matrice:
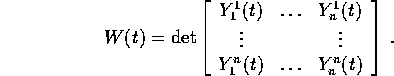
Il wronskiano di 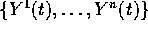 è il volume orientato del
parallepipedo formato dai vettori
è il volume orientato del
parallepipedo formato dai vettori 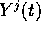 , nel senso della misura di
volume e dell'orientamento fissati dalla base di
, nel senso della misura di
volume e dell'orientamento fissati dalla base di 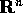 rispetto alla
quale sono calcolate le componenti
rispetto alla
quale sono calcolate le componenti 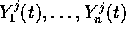 .
.
Teorema del determinante wronskiano :
Siano 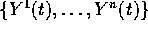 soluzioni di
soluzioni di 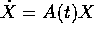 : allora
: allora
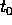 ;
;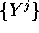 formano un
sistema fondamentale di soluzioni se e solo se
formano un
sistema fondamentale di soluzioni se e solo se
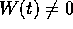 per un
per un 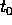 .
.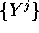 formano un sistema fondamentale di soluzioni, allora
il loro wronskiano W(t) soddisfa l'equazione
formano un sistema fondamentale di soluzioni, allora
il loro wronskiano W(t) soddisfa l'equazione
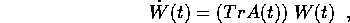
ovvero 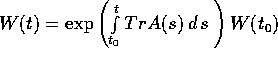 .
.
Dimostrazione:
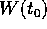 influenza quello di W(t) tramite il flusso
influenza quello di W(t) tramite il flusso
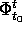 del sistema, che è un isomorfismo
del sistema, che è un isomorfismo 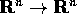 per
ogni t: poiché
per
ogni t: poiché 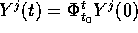 ,
,
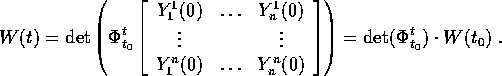
Sviluppando in serie la soluzione di 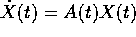 si ottiene
si ottiene
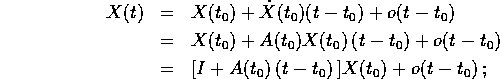
ottenendo così anche lo sviluppo della matrice di 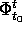
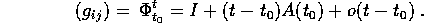
I coefficienti 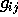 sono di ordine 0 rispetto a
sono di ordine 0 rispetto a 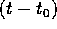 solamente per i=j: perciò nel determinante di
solamente per i=j: perciò nel determinante di 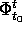 ciascuno
dei prodotti di n termini dei
ciascuno
dei prodotti di n termini dei 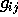 contribuisce al coefficiente
di
contribuisce al coefficiente
di 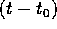 con gli elementi della diagonale
con gli elementi della diagonale  , e lo sviluppo
in serie del determinante risulta
, e lo sviluppo
in serie del determinante risulta
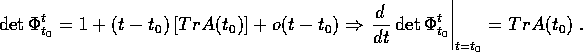
Dunque per un generico t
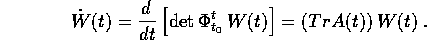
Nel caso a coefficienti costanti si ottiene la formula della traccia .
Esempio:

La posizione di equilibrio 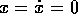 non è mai
asintoticamente stabile .
non è mai
asintoticamente stabile .
Infatti il sistema associato all'equazione è

se l'origine fosse asintoticamente stabile, il wronskiano del sistema
sarebbe infinitesimo per 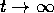 , mentre per qualunque
, mentre per qualunque
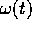 assegnata si ha Tr A(t)=0 e quindi
assegnata si ha Tr A(t)=0 e quindi
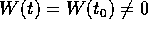 .
.
Problema Nel caso con dissipazione, l'altalena con piccole oscillazioni è modellata dall'equazione
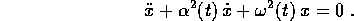
In quali casi la posizione di equilibrio 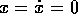 è
asintoticamente stabile ?
(Soluzione)
è
asintoticamente stabile ?
(Soluzione)