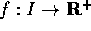 una funzione reale non negativa, definita su un aperto
una funzione reale non negativa, definita su un aperto
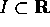 . Se la f è dominata dal suo integrale,
nel senso che per due costanti
. Se la f è dominata dal suo integrale,
nel senso che per due costanti 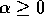 ,
, 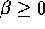 ,
,
Sommario La dipendenza delle soluzioni dalle condizioni iniziali è non solo continua, ma ha una costante di Lipschitz che può essere calcolata a partire dalla costante di Lipschitz del secondo membro, e che cresce esponenzialmente al crescere dell'intervallo di tempo. Questo consente in molti casi, tra cui quello lineare, di dimostrare che le soluzioni non vanno all'infinito in un tempo finito.
Teorema della diseguaglianza di Gronwall :
Sia 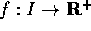 una funzione reale non negativa, definita su un aperto
una funzione reale non negativa, definita su un aperto
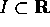 . Se la f è dominata dal suo integrale,
nel senso che per due costanti
. Se la f è dominata dal suo integrale,
nel senso che per due costanti 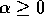 ,
, 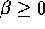 ,
,
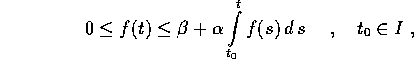
allora è dominata, per ogni  , da una funzione esponenziale:
, da una funzione esponenziale:

Dimostrazione:
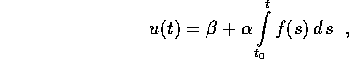
poiché 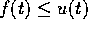 il risultato segue da una maggiorazione per
u(t).
il risultato segue da una maggiorazione per
u(t).
Evidentemente u è derivabile e 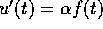 . Se
. Se 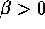 ,
anche u(t)>0 e da
,
anche u(t)>0 e da
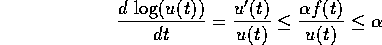
si ottiene, integrando entrambi i membri,
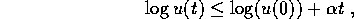
ossia 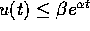 .
.
Il risultato può inoltre essere applicato ad una successione infinitesima
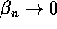 : associando a ciascun
: associando a ciascun 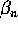 una funzione
una funzione 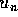 come
sopra e passando al limite per
come
sopra e passando al limite per 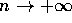 si ottiene la tesi per il
caso
si ottiene la tesi per il
caso 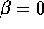
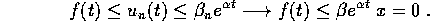
Il teorema che segue applica la diseguaglianza di Gronwall per fornire
dettagli precisi sulla dipendenza dai dati iniziali del flusso 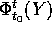 di un sistema dinamico.
di un sistema dinamico.
Teorema di continuità del flusso :
Siano 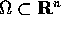 un aperto,
un aperto, 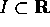 un intervallo e
un intervallo e
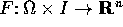 un
campo vettoriale uniformemente lipschitziano nella prima
variabile, con costante di Lipschitz L. Se Y(t) e Z(t) sono
soluzioni dell'equazione
un
campo vettoriale uniformemente lipschitziano nella prima
variabile, con costante di Lipschitz L. Se Y(t) e Z(t) sono
soluzioni dell'equazione
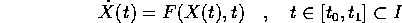
passanti, rispettivamente, per 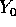 e
e 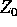 al tempo
al tempo  ,
allora
,
allora
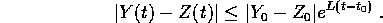
Dimostrazione:
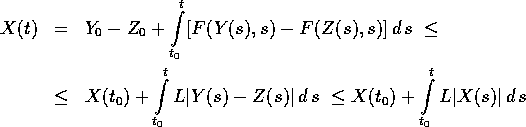
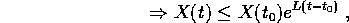
ovvero la tesi.
La diseguaglianza di Gronwall consente di mostrare che, nel caso particolare di un sistema lineare, la soluzione - indipendentemente dalla condizione iniziale - è definita in tutto l'intervallo in cui sono definiti i coefficienti:
Teorema di esistenza (caso lineare) :
Se 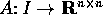 è una matrice a coefficienti continui
sull'intervallo aperto
è una matrice a coefficienti continui
sull'intervallo aperto 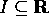 , il sistema
, il sistema
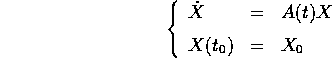
per ogni 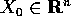 ha soluzione unica
ha soluzione unica 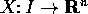 definita su
tutto I.
definita su
tutto I.
Dimostrazione:
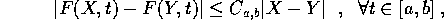
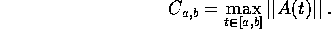
Inoltre per 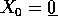 passa solo la soluzione costante
passa solo la soluzione costante
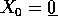 , definita su tutto I. Supponiamo dunque che
, definita su tutto I. Supponiamo dunque che
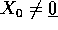 , in modo che
, in modo che 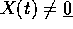 per ogni t
nell'intervallo
per ogni t
nell'intervallo 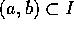 sul quale è definita, e mostriamo
che (a,b)=I.
sul quale è definita, e mostriamo
che (a,b)=I.
La linearità di A permette di ragionare per assurdo: se fosse
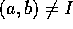 si potrebbe prolungare X(t) dapprima fino alla
chiusura [a,b], quindi anche oltre gli estremi dell'intervallo
(utilizzandoli per definire nuove condizioni iniziali). Per prolungare
X(t) fino a b, infatti, si osserva che
si potrebbe prolungare X(t) dapprima fino alla
chiusura [a,b], quindi anche oltre gli estremi dell'intervallo
(utilizzandoli per definire nuove condizioni iniziali). Per prolungare
X(t) fino a b, infatti, si osserva che
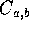 ;
; 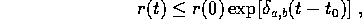
in quanto si può applicare la diseguaglianza di Gronwall alla diseguaglianza
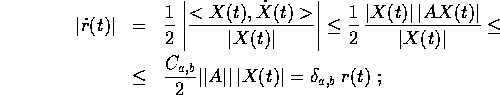
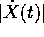 ;
;
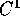 fino a b; infine, la funzione Y(t) che per
fino a b; infine, la funzione Y(t) che per  coincide con X(t) e per t>b coincide con la soluzione del problema
coincide con X(t) e per t>b coincide con la soluzione del problema
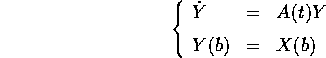
risolve anche il problema iniziale ed è definita su un aperto
strettamente più grande di (a,b), che quindi non può essere
l'intervallo massimale di definizione della soluzione passante per
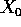 .
.