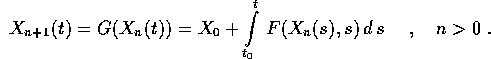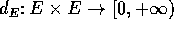 , e sia
, e sia 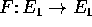 un'applicazione dello spazio in se stesso.
un'applicazione dello spazio in se stesso.
Si dice che F è una contrazione se esiste una costante L, con 0<L<1, tale che
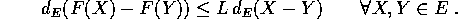
Sommario Purché siano soddisfatte opportune ipotesi di regolarità del secondo membro, che sono certamente soddisfatte dai sistemi dinamici continui, i sistemi di equazioni differenziali ordinarie hanno soluzione per ogni data condizione iniziale.
Definizione:
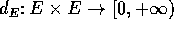 , e sia
, e sia 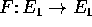 un'applicazione dello spazio in se stesso.
un'applicazione dello spazio in se stesso.
Si dice che F è una contrazione se esiste una costante L, con 0<L<1, tale che
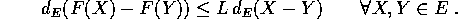
Definizione:
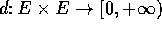 . Una successione
. Una successione 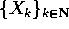 in E si dice
successione di Cauchy se
in E si dice
successione di Cauchy se
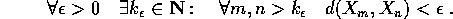
Si dice che E è uno spazio metrico completo se ogni successione di Cauchy è convergente.
Queste definizioni valgono sia per gli spazi a dimensione
finita, come 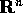 , sia per gli spazi di funzioni che hanno
dimensione infinita , nel senso che sono spazi vettoriali ma non
hanno un numero finito di generatori.
, sia per gli spazi di funzioni che hanno
dimensione infinita , nel senso che sono spazi vettoriali ma non
hanno un numero finito di generatori.
Esempio:
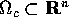 , lo spazio delle funzioni
continue su
, lo spazio delle funzioni
continue su 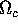
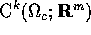 è completo rispetto
alla metrica della convergenza uniforme
è completo rispetto
alla metrica della convergenza uniforme
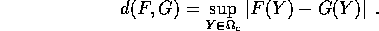
Teorema del punto unito :
Se G una contrazione di uno spazio metrico completo E, G ha un
punto unito unico, cioè esiste uno ed un solo 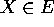 tale
che G(X)=X.
tale
che G(X)=X.
Dimostrazione:
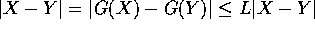 con L<1 segue
|X-Y|=0.
con L<1 segue
|X-Y|=0.
Il punto fisso è costruito per approssimazioni successive , come limite della successione

che, comunque sia scelto il punto iniziale 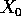 , converge nello
spazio metrico completo E in quanto successione di Cauchy:
, converge nello
spazio metrico completo E in quanto successione di Cauchy:
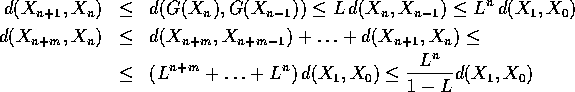
dove l'ultimo passaggio è legittimo perché L<1.
Definizione:
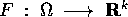 si dice
lipschitziana su
si dice
lipschitziana su 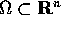 se esiste una costante
L>0 tale che, per ogni coppia X,Y di punti di
se esiste una costante
L>0 tale che, per ogni coppia X,Y di punti di 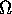 :
:
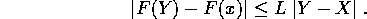
Ogni numero L che soddisfa a questa condizione si chiama costante di Lipschitz per la funzione F.
Una contrazione è una funzione lipschitziana di uno spazio in se stesso, con L<1.
Una funzione lipschitziana è anche continua, anzi
uniformemente continua , in quanto per ogni 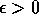 esiste
un
esiste
un 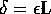 tale che
tale che 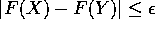 per ogni
coppia (X,Y) con
per ogni
coppia (X,Y) con 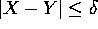 . Se
. Se 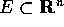 , la
lipschizianità nel punto Y equivale alla limitatezza del rapporto
incrementale nel punto Y in direzione X-Y; si può mostrare che
implica la differenziabilità in quasi tutti i punti di E (cioè
a meno di insiemi di misura nulla). Viceversa, ogni funzione F
differenziabile di classe
, la
lipschizianità nel punto Y equivale alla limitatezza del rapporto
incrementale nel punto Y in direzione X-Y; si può mostrare che
implica la differenziabilità in quasi tutti i punti di E (cioè
a meno di insiemi di misura nulla). Viceversa, ogni funzione F
differenziabile di classe 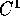 su di un aperto
su di un aperto 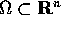 è localmente lipschitziana , nel senso che la diseguaglianza
di Lipschitz è soddisfatta in ogni aperto limitato
è localmente lipschitziana , nel senso che la diseguaglianza
di Lipschitz è soddisfatta in ogni aperto limitato 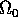 con
chiusura contenuta in
con
chiusura contenuta in 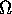 : come costante di Lipschitz si può
prendere la somma dei massimi moduli di tutte le derivate parziali di F
sulla chiusura di
: come costante di Lipschitz si può
prendere la somma dei massimi moduli di tutte le derivate parziali di F
sulla chiusura di 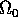 .
.
Teorema di esistenza e unicità :
Siano 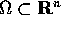 un aperto,
un aperto, 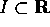 un
intervallo e
un
intervallo e 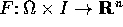 un campo vettoriale
uniformemente lipschitziano nella prima variabile, ovvero tale
che, per una costante
un campo vettoriale
uniformemente lipschitziano nella prima variabile, ovvero tale
che, per una costante 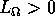 ,
,
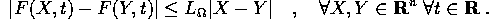
Allora se 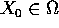 e
e 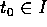 , esistono un intorno
, esistono un intorno
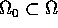 di
di 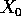 ed un intorno
ed un intorno 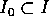 di
di 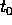 tali che il problema alle condizioni iniziali
tali che il problema alle condizioni iniziali
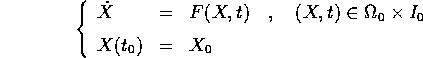
ha soluzione unica, ovvero esiste localmente il
flusso integrale 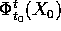 dell'equazione. Inoltre la soluzione dipende
con continuità dalla condizione iniziale
dell'equazione. Inoltre la soluzione dipende
con continuità dalla condizione iniziale 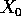 .
.
Dimostrazione:
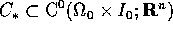 di funzioni continue come
di funzioni continue come
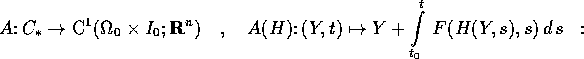
infatti, se esiste una funzione H continua su 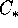 tale che
A(H)=H, allora la curva
tale che
A(H)=H, allora la curva 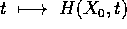 è di classe
è di classe
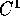 per ogni
per ogni 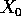 , e la funzione X(t) definita da
, e la funzione X(t) definita da

risolve il problema dato poiché 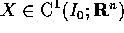 e
e
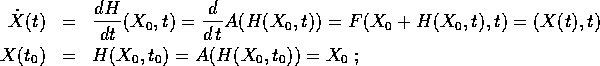
perciò 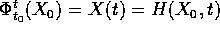 , ed in particolare la
continuità di H rispetto alla prima variabile implica quella del
flusso rispetto alla condizione iniziale. Applicando la
diseguaglianza di Gronwall si può mostrare che il flusso
è addirittura lipschitziano in
, ed in particolare la
continuità di H rispetto alla prima variabile implica quella del
flusso rispetto alla condizione iniziale. Applicando la
diseguaglianza di Gronwall si può mostrare che il flusso
è addirittura lipschitziano in 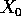 (ma la costante di Lipschitz
diverge con il tempo).
(ma la costante di Lipschitz
diverge con il tempo).
Per dimostrare che H ha un punto fisso, cioè che esistono
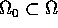 e
e 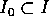 per i quali
per i quali
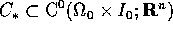 completo
rispetto alla metrica della convergenza uniforme
completo
rispetto alla metrica della convergenza uniforme
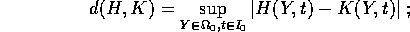
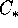 in se stesso;
in se stesso;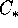 .
.
Poniamo 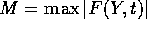 per
per 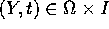
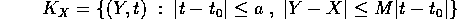
sono contenuti in 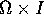 per
per 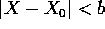 . Posto
. Posto
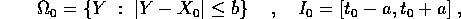
sia 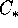 l'insieme delle funzioni a crescita sublineare in t
intorno a
l'insieme delle funzioni a crescita sublineare in t
intorno a 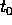
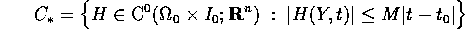
(se 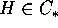 , risulta
, risulta 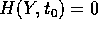 ).
).
L'insieme 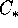 è chiuso rispetto alla metrica della convergenza
uniforme, poiché la convergenza rispetto ad essa implica la
convergenza puntuale, e se
è chiuso rispetto alla metrica della convergenza
uniforme, poiché la convergenza rispetto ad essa implica la
convergenza puntuale, e se 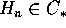 anche
anche 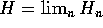 verifica
la diseguaglianza
verifica
la diseguaglianza 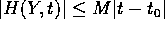 , quindi
, quindi 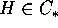 . Perciò
. Perciò
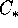 , in quanto sottoinsieme chiuso dello spazio metrico completo
, in quanto sottoinsieme chiuso dello spazio metrico completo
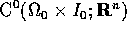 , è completo.
, è completo.
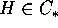 , allora
, allora
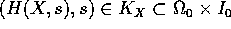 per
per 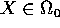 e
e
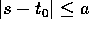 ; in tal caso ha senso F(H(x,s),s) e l'operatore A
è ben definito. Inoltre
; in tal caso ha senso F(H(x,s),s) e l'operatore A
è ben definito. Inoltre
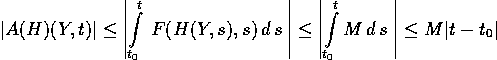
implica che 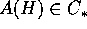 .
.
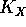 (quindi
l'altezza del cilindro
(quindi
l'altezza del cilindro 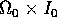 ) sufficientemente piccola
da rendere A una contrazione su
) sufficientemente piccola
da rendere A una contrazione su 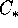 : poiché infatti
: poiché infatti
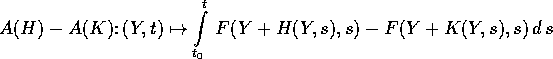
per la lipschizianità di F si ha
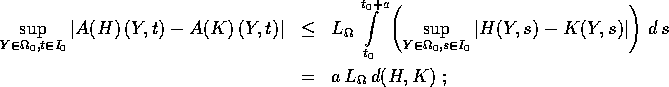
basta che sia 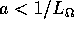 .
.
La dimostrazione del teorema precedente è costruttiva
(un'applicazione pratica è il ragionamento che conduce alla
definizione dell'esponenziale di matrice ). Il teorema delle
contrazioni, infatti, mostra l'esistenza di un punto fisso
dell'operatore 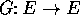 sullo spazio metrico completo E per
mezzo della successione definita per ricorrenza da
sullo spazio metrico completo E per
mezzo della successione definita per ricorrenza da

nel caso precedente, alla soluzione del problema alle condizioni iniziali converge la successione di funzioni