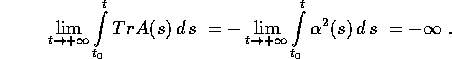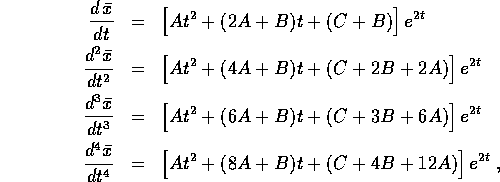
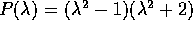. Nel primo caso, essendo 
e 
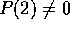, si applica il teorema dell'isomorfismo tra quasipolinomi , cercando una soluzione particolare del tipo 
: 
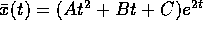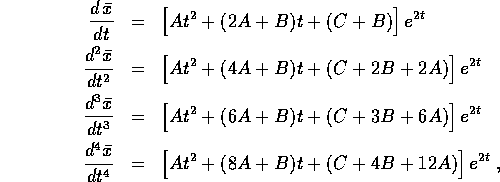
da cui, per sostituzione nell'equazione,
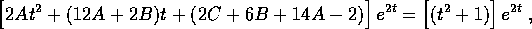
ovvero
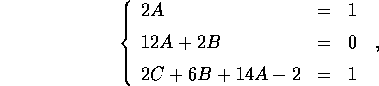
quindi la soluzione generale x(t) si ottiene da
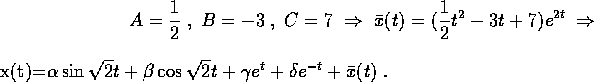
Nel secondo caso, essendo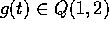 
e P(2)=0, si applica il teorema dell'abbassamento di grado dei quasipolinomi .
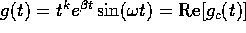, con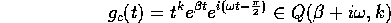 
e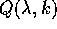 
indicante i quasipolinomi a coefficienti complessi.
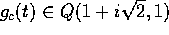e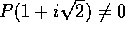 
; quindi la soluzione particolare complessa è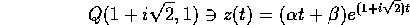 
con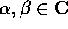 
da determinare per sostituzione; infine la soluzione particolare 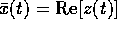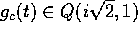è 
.
e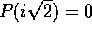 
, e si può applicare il metodo delle ampiezze compless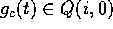e.
e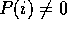 
; la soluzione particolare è ancora del tipo 
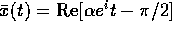con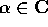 
, ovvero 
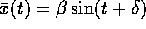per 
.
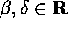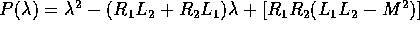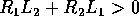, e 
e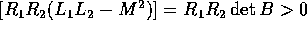 
.
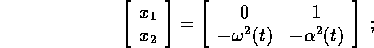
l'origine è asintoticamente stabile se e solo se il wronskiano del sistema è infinitesimo per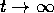 
, ovvero se
