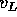Soluzioni del capitolo 7

PROBLEMA 7.1   Al lancio, se la velocità ha modulo :

mentre sull'orbita di trasferimento dopo il lancio

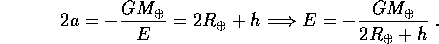
Eguagliando le due espressioni per E si ricava :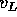

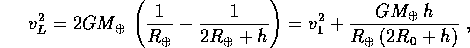
in cui il secondo termine esprime il fatto che il lancio avviene ad una velocità maggiore della prima velocità cosmica. All'apogeo 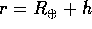la stessa orbita ha velocità 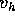, tale che il momento angolare è uguale a quello al lancio:

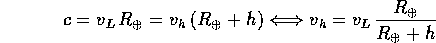
mentre l'orbita circolare ha velocità 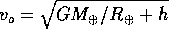, perciò bisogna eseguire all'apogeo una manovra per incrementare la velocità di 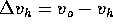. In conclusione l'incremento di velocità totale è

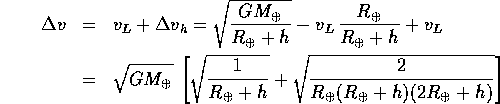
ed il rapporto con la prima velocità cosmica è

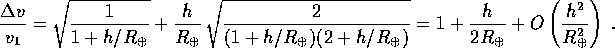
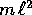PROBLEMA 7.24   Raccogliendo il fattore costante (che non influisce sulle equazioni di Lagrange) si trova una funzione di Lagrange riscalata L che dipende da due parametri positivi 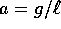e b=k/m: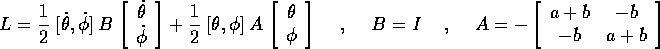

per cui le equazioni di Lagrange sono:

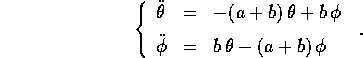
La soluzione si trova dagli autovalori di 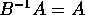, che sono 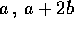, e dagli autospazi che sono le diagonali: passiamo quindi in coordinate :

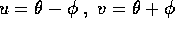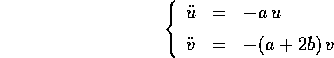
mettendo in evidenza le oscillazioni proprie con frequenz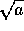e e 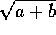; si nodi che l'oscillazione propria in cui i due pendoli sono in fase ha la stessa frequenza che i pendoli avrebbero se fossero disaccoppiati, mentre l'oscillazione propria in antifase ha una frequenza maggiore, tanto più alta quanto forte è l'accoppiamento b=k/m.