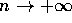7.3 CORPO RIGIDO LIBERO

 

Sommario Le equazioni di moto di un corpo rigido sono integrabili. Gli integrali primi dell'energia e del momento angolare possono essere espressi in funzione della velocità angolare, in un sistema di riferimento fisso col corpo; da questo si deducono le equazioni di movimento nella forma di Eulero, e la traiettoria descritta dal vettore velocità angolare. La teoria può essere sviluppata nel caso di un sistema rigido composto da un numero finito n di corpi puntiformi, e poi estesa ai corpi continui con un passaggio al limite per 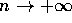. Per un corpo con simmetria assiale le soluzioni sono esprimibili in modo semplice.

Isometrie

Consideriamo un sistema rigido   di n corpi puntiformi  con masse 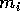e posizioni 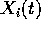; il concetto di rigidità è espresso con il vincolo che tutte le distanze fra i punti restino costanti:

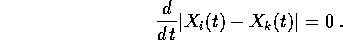
Un sistema rigido di corpi puntiformi fornisce un modello semplice per un corpo rigido ; in seguito presenteremo un modello continuo: come vedremo, le equazioni che descrivono la dinamica del corpo rigido non risentiranno della scelta del modello.

Consideriamo la trasformazione che manda le condizioni iniziali 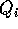(ad un tempo arbitrario, supponiamo 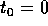) nelle posizioni al tempo t:

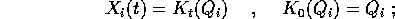
supponiamo che la trasformazione 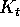sia una isometria  , cioè che sia una trasformazione definita su tutto 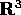che ne conserva la distanza di ogni coppia di punti; supponiamo inoltre che vi sia dipendenza differenziabile (almeno 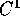) sia da 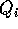che da t. Per le isometrie esiste una caratterizzazione geometrica molto precisa, che consente di descrivere lo spazio delle configurazioni del sistema rigido.

Teorema delle rotazioni di Eulero :  Ogni isometria è lineare, e precisamente è composizione di una traslazione e di una rotazione. Ogni isometria con un punto fisso ha un asse  , cioè una retta di punti fissi.

Dimostrazione:

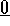Consideriamo il punto origine del sistema di coordinate in cui vengono assegnate le condizioni iniziali 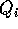: allora la curva differenziabile



descrive il moto dell'origine, e la differenza 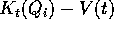è, per ogni t, un'isometria con l'origine come punto fisso.

Un'isometria con punto fisso è necessariamente una trasformazione lineare, poiché conserva la somma di vettori (la regola del parallelogramma è interamente descrivibile in termini di lunghezze) e la moltiplicazione per scalare (descrivibile in termini del processo di misura). Perciò per ogni t esiste una matrice 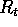tale che



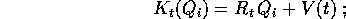
la condizione di conservazione delle distanze



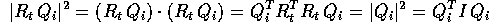
impone che la forma quadratica definita da 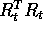coincida con quella definita da I, cioè 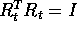. La matrice 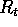è quindi ortogonale, e 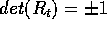: utilizzando l'ipotesi di continuità rispetto a t, da 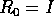si ottiene che 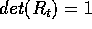. Quindi l'isometria è composizione di una rotazione  



con una traslazione  



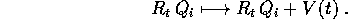
L'esistenza di un asse è conseguenza di una proprietà di tutte le rotazioni R: poiché 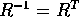ha gli stessi autovalori di R, se 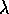è un autovalore di R, anche 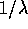lo è. In uno spazio di dimensione dispari, questo implica che ci sia sempre un autovalore 1, e quindi un asse di punti fissi.

 C.D.D.

Come per ogni trasformazione di coordinate, l'applicazione 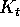ha due interpretazioni: come movimento rigido  , cioè come spostamento di un sistema di corpi in un sistema di coordinate fisso (inerziale ) dalle condizioni iniziali 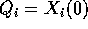allo stato corrente 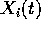, oppure come cambiamento di coordinate dipendente dal tempo, per cui i punti 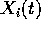sono costantemente contrassegnati dalle coordinate fisse con il corpo 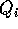  . Noi usiamo il secondo punto di vista, per cui le velocità generalizzate 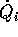sono nulle, mentre nel sistema di riferimento inerziale le velocità 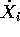non si annullano e devono essere calcolate tenendo conto delle derivate della matrice di rotazione e del vettore traslazione. Si utilizza allora la regola della velocità angolare  :

Lemma:

Per un movimento rigido



dove R=R(t) e V=V(t) dipendono in modo 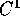dal tempo, esiste un vettore velocità angolare 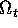  , in coordinate fisse con il corpo, tale che



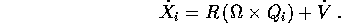
Inoltre l'accelerazione si esprime come



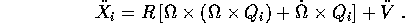
Dimostrazione del lemma:

Derivando si ottiene



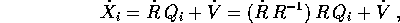
dove la matrice 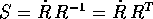è antisimmetrica, come si deduce derivando :



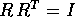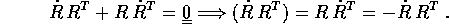
La matrice antisimmetrica S è associata ad un vettore assiale   W, nel senso che la moltiplicazione a sinistra per S è interpretabile come un prodotto vettore



come è facile verificare per confronto fra i coefficienti del vettore e della matrice:



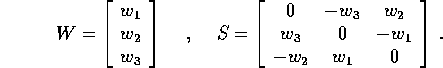
Il prodotto vettore e la matrice antisimmetrica sono due rappresentazioni dello stesso operatore lineare.

Sostituendo nella formula della velocità nel sistema inerziale



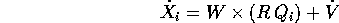
si ricava la velocità angolare 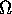nel sistema di coordinate fisso con il corpo:



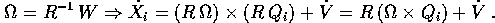
Derivando infine rispetto al tempo si ottiene la formula per l'accelerazione

C.D.D. lemma

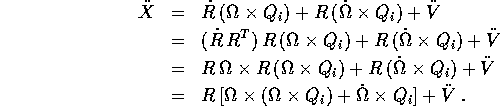
La relazione tra la rotazione dipendente dal tempo R=R(t)t ed il vettore assiale  W=W(t) (oppure 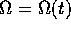), che ne esprime la velocità angolare, può essere utilizzata per parametrizzare globalmente il gruppo SO(3) di tutte le rotazioni:

Teorema delle rotazioni infinitesimali :  Tutte e sole le matrici ortogonali di dimensione dispari sono esprimibili come esponenziale di matrici antisimmetriche.

Dimostrazione:

Per ogni matrice quadrata S valgono le proprietà dell'esponenziale di matrice 



la prima segue dalla definizione dell'esponenziale come serie, la seconda dal teorema della somma degli esponenti 



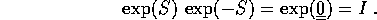
Se S è una matrice antisimmetrica ( 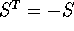) ed 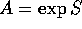, allora A è ortogonale:



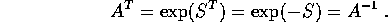
Viceversa, sia A una matrice ortogonale di dimensione dispari; come dimostrato dal teorema delle rotazioni di Eulero , A rappresenta una rotazione intorno ad un asse z. In un riferimento cartesiano ortogonale avente l'ultimo asse coordinato lungo z, la rotazione `e espressa dalla matrice 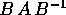(con 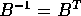) della forma



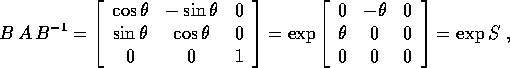
quindi 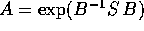, dove 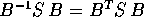è antisimmetrica.

 C.D.D.

Il gruppo delle rotazioni SO(3) è una varietà differenziabile di dimensione 3, e l'esponenziale di matrice ne fornisce una carta coordinata, almeno nell'intorno dell'identità I.

Una matrice antisimmetrica ha traccia zero, ed una matrice di rotazione ha determinante 1. Questo è un caso particolare della formula della traccia  :

che deriva semplicemente dal fatto che gli autovalor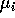i di 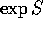sono legati a quelli 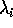di S da 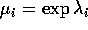, e con la stessa molteplicità; ora 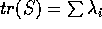, mentre .

Energia cinetica e momento angolare

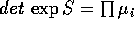Sia per scrivere le equazioni di moto di un corpo rigido, sia per trovarne gli integrali primi, dobbiamo trovarne l'espressione dell'energia cinetica  e del momento angolare . Nel caso del sistema rigido  di n corpi puntiformi, possiamo partire dalle espressioni in coordinate cartesiane, che sono semplicemente le stesse del caso di n corpi in moto libero:

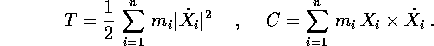
L'ipotesi del sistema rigido si traduce nell'espressione della posizione e della velocità in funzione delle coordinate fisse con il corpo e della velocità angolare:

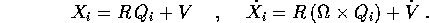
A questo punto basta sostituire: per l'energia cinetica

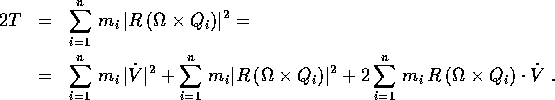
Se supponiamo che l'origine del sistema di coordinate 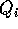sia nel centro di massa , cioè

allora il terzo termine nella formula dell'energia cinetica si annulla, e sfruttando il fatto che R, essendo una rotazione, è anche un'isometria, si ha

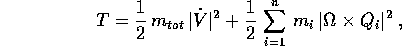
dove 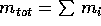è la massa totale. In conclusione l'energia cinetica si può esprimere come somma di un termine che dipende solo dalla velocità di traslazione del centro di massa, più un termine, dipendente dalla rotazione attorno al centro di massa, che, essendo una forma quadratica omogenea nella 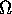, può essere espresso mediante una matrice simmetrica :

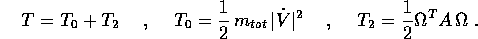
Questa decomposizione era già stata ottenuta per il moto di n corpi puntiformi indipendenti; ciò che è nuovo è l'espressione di 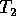in funzione della velocità angolare nel riferimento fisso col corpo .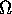

Per il momento angolare nel riferimento del centro di massa, con la stessa sostituzione si ha

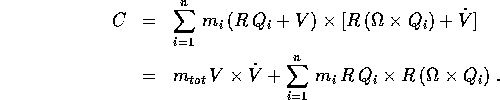
Quindi il momento angolare si decompone in due parti, una delle quali è il momento angolare di un corpo puntiforme di massa 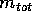che si muove con il centro di massa del sistema:

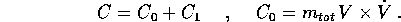
Il secondo termine si esprime in modo più semplice nel sistema di riferimento fisso con il corpo: infatti le rotazioni preservano anche i prodotti vettore, nel senso che

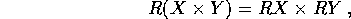
quindi

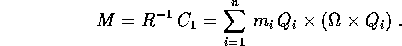
La formula del momento angolare M (nel sistema fisso con il corpo) è lineare nella velocità angolare 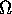, quindi si può esprimere nella forma 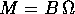, dove B è una matrice 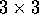che dipende solo dalle masse 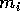e dalla loro posizione nel sistema di riferimento fisso nel corpo .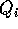

Teorema del tensore d'inerzia :  Se l'energia cinetica di un sistema rigido di n corpi (rispetto al centro di massa, oppure con centro di massa fisso) si esprime come

(con 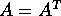), e se il vettore M, che è il momento angolare 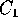(rispetto al centro di massa, oppure con centro di massa fisso) nel riferimento fisso con il corpo, si esprime come

allora le due matrici A e B sono uguali.

Dimostrazione:

Calcoliamo il prodotto scalare :



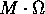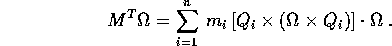
Permutando ciclicamente nel prodotto triplo   (che è il determinante dei tre vettori) si ottiene



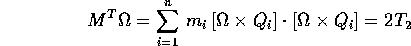
da cui



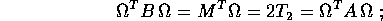
le due matrici A e B esprimono perciò la stessa forma quadratica. Inoltre, applicando ancora la permutazione del prodotto triplo



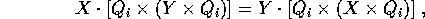
si ricava che B è simmetrica: perciò le due matrici simmetriche A e B, che definiscono la stessa forma quadratica, sono uguali.

 C.D.D.

Definizione:

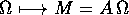La matrice A=B del teorema precedente si chiama tensore d'inerzia   del sistema rigido di n corpi; l'applicazione lineare si chiama operatore d'inerzia  .

Il momento d'inerzia   di un sistema rispetto all'asse di versore N è



perciò l'energia cinetica del sistema in funzione della velocità angolare 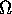(in coordinate fisse con il corpo) è



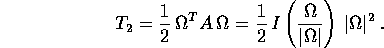
Il nome ``tensore'' è riferito alla legge di trasformazione della matrice A al cambiare del sistema di riferimento: infatti A viene usata come matrice simmetrica di una forma quadratica nella definizione di una quantità come 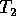che non dipende dal sistema di riferimento. Se, sempre restando fisso con il corpo, il sistema di coordinate è sottoposto ad una trasformazione lineare con matrice S, allora il tensore di inerzia si trasforma come .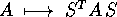

Per calcolare i momenti d'inerzia conviene usare l'espressione in cui compaiono le coordinate dei singoli punti. Se i vettori 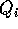delle posizioni (fisse con il corpo) dei punti di massa 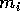hanno, rispetto alla base ortonormale 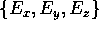, le coordinate 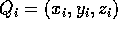, allora

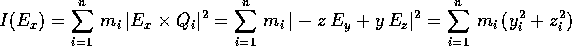
e analogamente

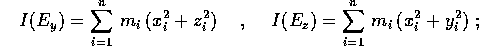
queste formule si esprimono geometricamente dicendo che nel momento d'inerzia rispetto ad un asse ogni corpo puntiforme contribuisce con la sua massa moltiplicata per il quadrato della distanza dall'asse.

Per calcolare i termini del tensore d'inerzia fuori dalla diagonale occorre utilizzare le relazioni tra prodotto scalare 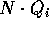, prodotto vettore 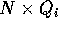ed angolo 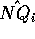tra versore dell'asse e vettori posizione:

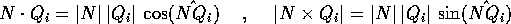
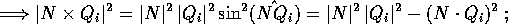
per un versore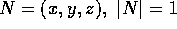

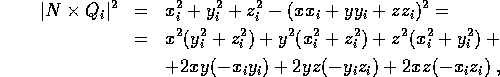
ed esprimendo questa forma quadratica in N mediante una matrice simmetrica e sommando rispetto ad i si ricava la matrice dell'operatore d'inerzia:

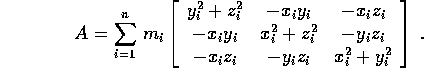
In generale, i termini fuori diagonale della matrice A non sono nulli. Poiché però la matrice A dell'operatore d'inerzia è simmetrica, per il teorema di diagonalizzazione delle forme quadratiche  ha autovalori reali ed è diagonalizzabile; essendo inoltre l'energia cinetica una forma quadratica definita positiva, i tre autovalori 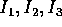 sono positivi e si indicano con il nome di momenti principali d'inerzia  , mentre gli autospazi, detti assi d'inerzia  , sono ortogonali. Dunque esiste un sistema di coordinate cartesiano ortogonale nel quale

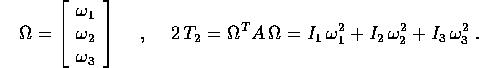
Esercizio Trovare il tensore d'inerzia dei seguenti sistemi rigidi di corpi:

(I)

Due corpi di masse .

(II)

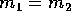Tre corpi di massa uguale che formano un triangolo equilatero di lato .

(III)

Quattro corpi di massa uguale m che formano un tetraedro di spigolo .

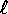Suggerimento: Individuare le simmetrie dei sistemi per usare riferimenti in cui i tensori d'inerzia risultino subito diagonali. Si noti che il caso (I) ha un operatore d'inerzia la cui matrice non è definita positiva: un ``vero'' corpo rigido deve contenere almeno tre punti.

Caso continuo

Vogliamo generalizzare la nozione di sistema rigido al caso ``continuo'', in cui la massa, anziché essere concentrata in un numero finito di punti, è distribuita in modo continuo in un volume. Un corpo rigido   è definito da un insieme 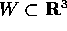e da una funzione densità  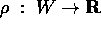 , tale che 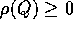per ogni .

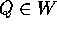Le condizioni a cui devono soddisfare sia W che 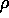possono variare a seconda dell'applicazione; l'unico requisito veramente importante è che l'integrale triplo che definisce la massa totale  

sia ben definito. Le condizioni perché questo sia vero dipendono dalla teoria dell'integrazione adottata. Noi ci limiteremo ad usare la teoria dell'integrazione di Riemann , per cui l'insieme W dovrà essere limitato e misurabile secondo Peano-Jordan , e la funzione 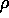dovrà essere continua e limitata.

Gli unici movimenti ammessi per un corpo rigido, per definizione, saranno isometrie, che per il teorema delle rotazioni di Eulero  avranno la forma

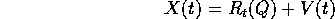
con la densità nel punto X ed al tempo t pari al valore 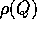nella condizione iniziale corrispondente.

Si tratta, in questo contesto, di definire l'energia cinetica, il momento angolare, il centro di massa, i momenti d'inerzia del corpo rigido. Come esempio più semplice consideriamo innanzitutto la definizione di massa totale: l'integrale di Riemann di 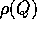su W è definito considerando l'insieme di tutte le possibili partizioni  di W in un numero finito di insiemi 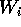di forma semplice, per esempio parallelepipedi con facce parallele agli assi coordinati di un fissato riferimento ortogonale; scelto arbitrariamente un punto 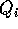in ciascun 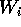, si calcola la somma

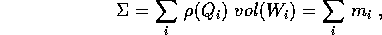
dove 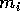è la massa attribuita al parallelepipedo, nell'ipotesi che abbia densità costante 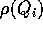. In altre parole, la somma relativa alla partizione corrisponde all'approssimazione per cui il corpo rigido continuo è descritto come sistema rigido di corpi puntiformi. 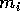Per il teorema di integrabilità delle funzioni continue  esiste il limite per il diametro dei parallelepipedi che tende a zero, e coincide con l'integrale che definisce la massa: può anche essere interpretato come il limite (indipendente dalle approssimazioni) della massa totale per il numero dei corpi puntiformi che tende all'infinito, con la massa di ciascuno che tende a zero (grazie all'ipotesi che la densità 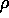sia limitata).

Allora, per esempio, l'ascissa del centro di massa  , per il corpo continuo, è

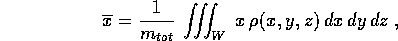
ovvero il limite di

analogamente si procede per 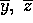. Similmente, le definizioni date per il corpo continuo si ottengono passando al limite (per il numero dei corpi che tende all'infinito, con la massa di ciascuno che tende a zero) delle corrispondenti definizioni applicate ad un sistema di corpi puntiformi.

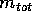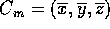Il passaggio al limite dai sistemi di corpi puntiformi ad un corpo continuo è una buona giustificazione intuitiva del procedimento: ciò non toglie che le definizioni di massa totale , centro di massa , energia cinetica, momento angolare, momento d'inerzia, eccetera, siano espresse in forma integrale.

Definizione:

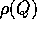Se X=X(Q,t) è la posizione occupata al tempo t dal punto del corpo rigido che a t=0 sta in Q (quindi la densità nel punto X ad ogni istante t è ), allora l'energia cinetica   ed il momento angolare   sono, rispettivamente

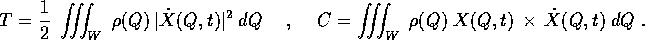
La generalizzazione al corpo rigido continuo dei risultati ottenuti per i sistemi rigidi di corpi puntiformi si ottiene, in sostanza, eseguendo sotto il segno di integrale triplo gli stessi calcoli che vengono eseguiti sotto il simbolo di sommatoria nel caso di un sistema rigido formato da un numero finito di corpi puntiformi. Finché si tratta di definizioni, come quelle di energia cinetica e di momento angolare, basta disporre di una definizione di integrale triplo. Alquanto più difficile sarebbe dimostrare che un corpo rigido continuo, con energia cinetica T ed energia potenziale delle forze esterne V, si muove secondo le soluzioni delle equazioni di Lagrange con lagrangiana  L=T-V. Questo richiede un sistema di ulteriori assiomi per la dinamica dei corpi continui che estende le leggi di Newton per il corpo puntiforme; vedi per esempio [Truesdell 91], capitolo I. Per semplificare l'esposizione, assumeremo le equazioni di Lagrange, e non quelle di Newton, come assioma o principio dinamico fondamentale nel caso del corpo rigido continuo. Al contrario, nel caso discreto abbiamo dimostrato che le equazioni di Lagrange sono equivalenti a quelle di Newton, come risulta dal teorema dei moti vincolati .

Sostituendo nelle definizioni di T,C le formule

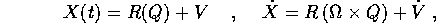
dove 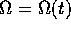è la velocità angolare  nel sistema di coordinate fisso con il corpo (quello delle coordinate Q), si ottiene per l'energia cinetica

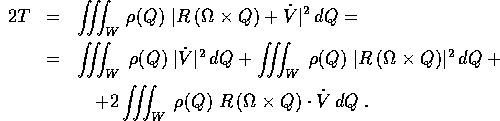
Se supponiamo che l'origine del sistema di coordinate delle 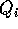sia nel centro di massa , cioè

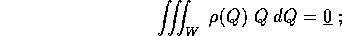
allora il terzo termine nella formula dell'energia cinetica si annulla, perché si possono portare fuori dal segno di integrale tutte le operazioni fatte con vettori costanti:

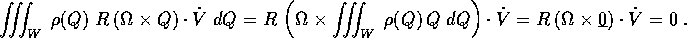
Sfruttando il fatto che R, essendo una rotazione, è anche un'isometria. si ha

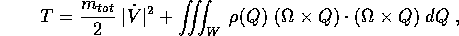
e, permutando ciclicamente il prodotto triplo, si può scrivere T anche nella forma

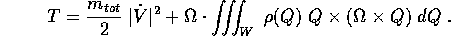
Per il momento angolare nel riferimento del centro di massa, con la stessa sostituzione si ricava

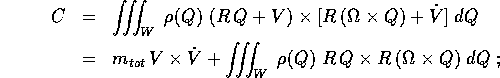
poiché infine 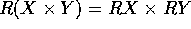, si trova

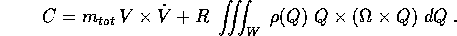
Definizione:

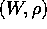L'operatore d'inerzia   del corpo rigido definito da è l'applicazione lineare definita dall'integrale



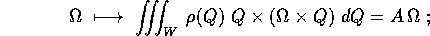
A è il tensore d'inerzia  . Il momento d'inerzia   relativo all'asse definito dal versore N è .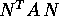

Segue immediatamente, dalle definizioni di centro di massa, energia cinetica, momento angolare e tensore d'inerzia per un corpo rigido, che valgono per un corpo continuo le formule già viste per un sistema rigido di corpi puntiformi:

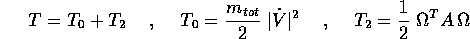
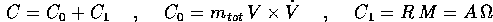
dove A è il tensore d'inerzia, cioè lo stesso integrale che compare sia nell'energia cinetica che nel momento angolare. Questo consente di svolgere esattamente con lo stesso procedimento le due teorie del sistema rigido di corpi puntiformi e del corpo rigido continuo.

Per esempio, svolgendo i calcoli in modo perfettamente analogo al caso del sistema di corpi puntiformi, si trova che il momento di inerzia rispetto all'asse z di un sistema di coordinate cartesiano ortogonale Q=(x,y,z) è l'integrale

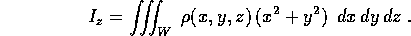
Gli esercizi sul centro di massa e sui momenti d'inerzia di un corpo rigido si riducono al calcolo di integrali tripli; ne elenchiamo soltanto alcuni, i cui risultati ci serviranno in seguito.

Esercizio Calcolare il tensore di inerzia dei seguenti solidi, supponendo costante la densità :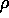

(I)

Una palla di raggio R.

(II)

Un cilindro pieno, circolare retto, di raggio R e altezza h.

(III)

Un cubo di lato R.

(IV)

Un ellissoide oblato di rotazione, con raggio equatoriale R e raggio polare R(1-f)<R.

La nozione di corpo continuo definita dalla sola funzione densità non è affatto la sola possibile. Per esempio, diversamente dai corpi ``uniformi'' definiti in questo modo, si possono immaginare continui con struttura, il cui stato non è specificato dalla sola funzione densità. Nella teoria dinamica del corpo rigido si considera solo il comportamento macroscopico del corpo, come se lo vedessimo soltanto dall'esterno; perciò per considerare perfettamente rigido il corpo si ritiene sufficiente prescrivere che la densità sia invariante nel tempo, trascurando ogni altra proprietà.

Integrabilità

Consideriamo un corpo rigido , il cui moto sia descritto dall'isometria

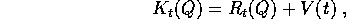
e che ha, nel riferimento fisso con il corpo stesso, velocità angolare 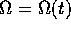 e momento angolare  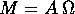; A è la matrice dell'operatore d'inerzia. Studiamo il moto di un corpo rigido libero  , cioè senza forze esterne. Allora la lagrangiana  si riduce all'energia cinetica:

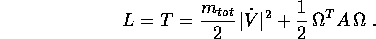
Si noti che questa formula della lagrangiana si applica sia al caso discreto che al caso continuo, naturalmente con una diversa definizione del tensore d'inerzia A.

Per scrivere le equazioni di moto del corpo rigido libero occorrerebbe parametrizzare lo spazio delle configurazioni con un sistema di coordinate lagrangiane , per esempio le coordinate del centro di massa e gli angoli di Eulero , ed esprimere la lagrangiana in funzione di queste. Tuttavia, il teorema di Noether  si può applicare indipendentemente dal sistema di coordinate impiegato. Poiché la lagrangiana è invariante per traslazione, allora il vettore quantità di moto è un integrale primo; poiché è invariante per rotazione, il vettore momento angolare è un integrale primo; inoltre, poiché la hamiltoniana non dipende dal tempo, ha un integrale dell'energia che coincide con l'energia cinetica. Questa argomentazione sarà resa più precisa dai teoremi seguenti.

Teorema della quantità di moto :  Il moto di traslazione del centro di massa del corpo rigido libero è rettilineo uniforme. Se l'origine del sistema di coordinate fisse nel corpo è il centro di massa, allora tale moto del centro di massa ha vettore traslazione V(t) costante:

Dimostrazione:

Usiamo un qualunque sistema di 6 coordinate lagrangiane che descrivano il moto del corpo rigido, con le prime tre che coincidono con le coordinate cartesiane V del centro di massa. La lagrangiana è



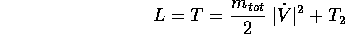
dove è necessario solamente sapere che 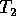non dipende né da V né da 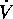. Allora le prime tre equazioni di Lagrange sono

 C.D.D.

Teorema del momento angolare :  Il vettore momento angolare è un integrale primo per il moto del corpo rigido libero.

Dimostrazione:

Possiamo supporre che il centro di massa sia fisso nell'origine dei sistemi di coordinate (sia quello fisso con il corpo, che quello inerziale). Infatti il cambiamento di coordinate tra un qualunque sistema inerziale e quello con origine nel centro di massa, per il teorema precedente, è un moto rettilineo uniforme, che non cambia le derivate seconde, e quindi mantiene la proprietà di inerzialità.

Nel caso di un sistema rigido di corpi puntiformi, si pò applicare direttamente il teorema di Noether  ad un gruppo ad un parametro di rotazioni attorno ad un asse passante per il centro di massa fisso. Poichè l'energia cinetica contiene soltanto le lunghezze delle velocità 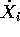, la lagrangiana del corpo rigido libero è invariante. Il corrispondente integrale primo è la componente del vettore momento angolare  lungo l'asse di rotazione, come nel caso del problema degli n corpi . Infatti, se il gruppo ad un parametro di rotazioni è:



con W un versore che indica l'asse di rotazione, allora



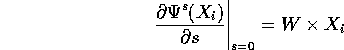
e l'integrale primo del teorema di Noether è:



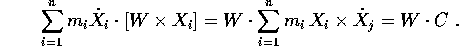
Il caso del corpo continuo si può trattare molto più facilmente disponendo di una parametrizzazione esplicita dello spazio delle configurazioni del corpo rigido; perciò la dimostrazione sarà completata nella sezione successiva.

Dimostrazione da completare.

La conseguenza più immediata dei due teoremi precedenti è che il problema del corpo rigido libero è integrabile . Questo potrebbe essere dimostrato verificando le ipotesi del teorema di Arnold-Jost ; infatti, per il corpo rigido libero nel sistema di riferimento con origine nel centro di massa, l'energia E=T, la lunghezza c del vettore momento angolare, ed una qualsiasi componente dello stesso, sono tre integrali primi in commutazione .

Tuttavia in questo caso è possibile descrivere le soluzioni in modo ancora più esplicito. Poniamoci nel sistema di riferimento in cui il centro di massa è fisso nell'origine, per cui 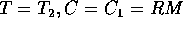; allora 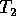è costante, e la lunghezza di M è costante (anche se non lo è la sua direzione) perché coincide con la lunghezza c di C:

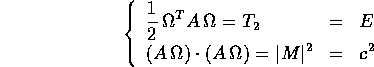
dove A è il tensore d'inerzia; o anche, in funzione di :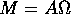

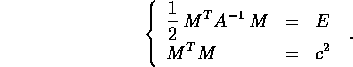
Per ogni fisso valore di E,c, questo sistema di due equazioni, nelle tre variabili che sono le componenti di M, descrive una curva che è l'intersezione di una sfera con un ellissoide (queste intersezioni sono rappresentate in Figura 7.8 per un valore fisso di E ed al variare di c). Perciò la traiettoria percorsa dal vettore momento angolare M(t) è nota, nel riferimento fisso con il corpo, e così quella della velocità angolare .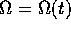

 
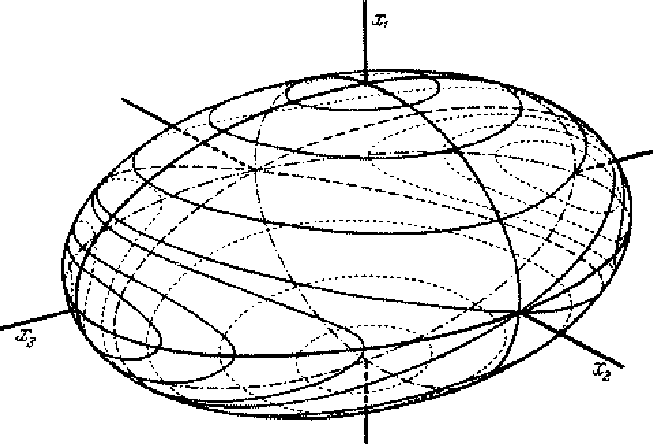
Figure 7.8:  Intersezioni di un ellissoide triassiale con sfere concentriche. Si noti che la soluzione in cui la velocità angolare è costante, e rivolta verso l'asse con momento principale intermedio, è instabile, mentre quelle rivolte verso gli assi con momenti principali massimi sono stabili.

Equazioni di Eulero

Si possono anche dedurre le equazioni di moto del vettore velocità angolare 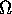, sfruttando il fatto che il momento angolare è un vettore di integrali primi. Supponendo il centro di massa fisso 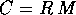, ed usando la regola della velocità angolare , si ha

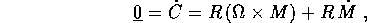
e moltiplicando per 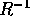si trova un sistema dinamico per M (o per ):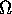

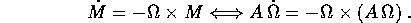
Le equazioni differenziali per l'evoluzione temporale di 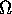sono le equazioni di Eulero  , che hanno una forma più semplice se la velocità angolare 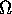è espressa in un sistema di coordinate che non solo è fisso con il corpo, ma ha assi coordinati lungo gli assi d'inerzia , per cui le componenti di 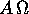sono :

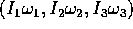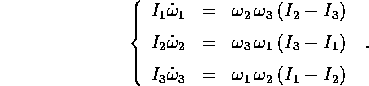
Le soluzioni delle equazioni di Eulero possono essere studiate in modo espressivo per mezzo dell'ellissoide d'inerzia   , una superficie utile per descrivere la distribuzione della massa nel corpo rigido. Il vettore appartiene all'ellissoide d'inerzia: dal fatto che un vettore normale a questo ellissoide nel punto Z è dato da

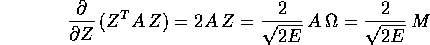
e che C=RM è un vettore fisso nel riferimento inerziale, segue che C individua un piano (ad esso perpendicolare) che è sempre tangente all'ellissoide nel suo punto d'intersezione con il vettore velocità angolare. In effetti il piano tangente all'ellissoide d'inerzia, visto nel riferimento inerziale, è sempre lo stesso, poiché

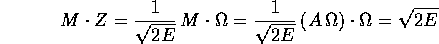
è un integrale primo, cioè è costante sulla soluzione. Si ottiene così il moto alla Poinsot   dell'ellissoide d'inerzia che si muove solidalmente con il corpo rigido libero, ma in modo da toccare un piano fisso nel punto d'intersezione con la velocità angolare.

Poiché il vettore 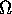definisce l'asse di rotazione istantaneo, sul quale la velocità di rotazione è nulla, si può descrivere il moto alla Poinsot dicendo che l'ellissoide d'inerzia ``rotola senza strisciare'' su un piano fisso nel sistema inerziale. Non bisogna però confondere il moto alla Poinsot con il moto di un solido che ``rotola senza strisciare'' su un piano; in effetti la forma della superficie esterna di un corpo può essere molto diversa dalla forma del suo ellissoide d'inerzia. Per esempio un tetraedro omogeneo ha per ellissoide d'inerzia una sfera, ma non può rotolare senza strisciare in nessun modo.

Nel caso in cui l'ellissoide d'inerzia di un corpo rigido sia una superficie di rotazione, con due momenti principali d'inerzia  uguali (diciamo ), le equazioni di Eulero si semplificano notevolmente:

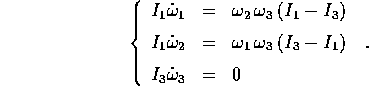
Se ne deduce che la componente 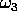della velocità angolare (lungo l'asse di simmetria dell'ellissoide d'inerzia) è costante. Quindi le prime due sono le equazioni di un oscillatore armonico 

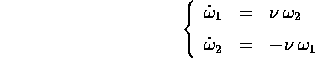
con frequenza

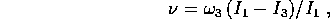
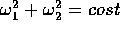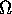le cui traiettorie sono circonferenze ; il vettore descrive un cono di precessione   nel sistema di coordinate fisso con il corpo. La frequenza con cui il vettore 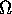gira attorno all'asse del cono è inferiore di un fattore 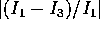alla frequenza di rotazione del corpo attorno allo stesso asse; il verso è lo stesso per un corpo oblato ( 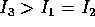), retrogrado per un corpo prolato ( 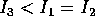). Ci sono anche soluzioni in cui 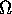è costante, se la direzione è quella dell'asse di simmetria dell'ellissoide d'inerzia.

Il vettore 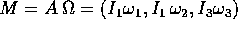percorre un altro cono; poiché M è la descrizione, nel sistema fisso con il corpo, di un vettore costante nel sistema inerziale, se ne deduce che l'asse di simmetria dell'ellissoide d'inerzia descrive ancora un cono nel sistema inerziale.

Problema Supponiamo che la Terra sia un ellissoide di rotazione di densità uniforme, con raggio polare più corto di un fattore 1-f del raggio equatoriale (una misura recente è 1/f= 298.257). Supponendo che il moto sia quello di un corpo libero rigido, descriverne il moto di rotazione, sapendo che la velocità angolare è .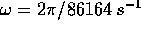

Se un corpo ha simmetria assiale  , cioè ha una forma ed una densità che non cambiano per effetto di rotazioni attorno ad un dato asse, allora l'ellissoide d'inerzia è di rotazione, e i due momenti principali d'inerzia in direzioni perpendicolari all'asse sono uguali tra loro. Però non è vero il contrario, cioè un corpo può avere 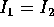senza avere simmetria assiale, come nel caso di un parallelepipedo rettangolo con due spigoli uguali.