


Next: 3.3 Stability
Up: 3. Results
Previous: 3.1 Hyperbolic cases
3.2 Resonant and ``pathological'' cases
Another group of troublesome cases is more heterogeneous. It again
consists mostly of resonant asteroids, but there are also a few
asteroids for which the determination of some proper value(s) was
seriously deteriorated due to other reasons. The approach we adopted
for these bodies is based upon the idea that all the data which could
have been computed, even with a low accuracy, might be useful at least
for statistical purposes; therefore, we decided to keep all these
bodies in the files, correcting very few of them in a special way,
whenever this was necessary. The users are warned that the
consultation of the files containing the RMS and the excursion in the
runnig box test is mandatory, at least before drawing any conclusion
from the values of the proper elements.
It is to be understood that we could not analyze in detail every
troublesome case found by our automated procedure. Thus, for most of
the bodies we only report the deteriorated quantities. We
defined as ``pathological'' all the cases for which one or more of the
following conditions were met:
Here 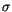 and
and 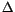 are standard deviation and maximum
excursion; the statistics for frequencies of perihelion g and
node s are given in arcsec/yr, these for the proper semimajor axis
ap in AU. In Table 2 we give a list of objects for which one or more
of the proper values, as derived from the basic 2 Myr integration,
exceeded the above thresholds.
are standard deviation and maximum
excursion; the statistics for frequencies of perihelion g and
node s are given in arcsec/yr, these for the proper semimajor axis
ap in AU. In Table 2 we give a list of objects for which one or more
of the proper values, as derived from the basic 2 Myr integration,
exceeded the above thresholds.
Table 2:
``Pathological'' cases for which some proper value(s) had
very large errors in 2 Myr run. The columns contain asteroid
identification, statistical parameters found to be excessively large,
and a remark on the specific dynamical features of the bodies. See
the text for notation and units.
| Asteroid |
Erroneous values |
Remark |
| 531 |
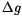 |
|
| 759 |
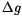 |
|
| 1263 |
 ; ;
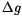 |
|
| 3480 |
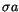 |
|
| 3579 |
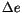 ; ;
 ; ;
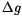 |
|
| 4112 |
 |
|
| 4915 |
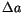 |
|
| 5222 |
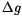 |
|
| 5330 |
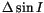 ; ;
 ; ;
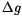 |
|
| 5765 |
 |
|
| 6626 |
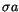 |
|
| 7306 |
 ; ;
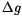 |
|
| 7598 |
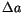 |
|
| 8009 |
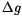 |
|
| 1977RD |
 |
|
| 1979OA |
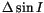 |
|
| 1981EJ40 |
 |
|
| 1981QN3 |
 |
2/1 |
| 1984LK |
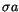 ; ;
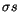 ; ;
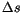 |
|
| 1987UW |
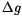 |
|
| 1991QG |
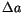 |
|
| 1991UC |
 |
e=0.0031 |
| 1993FB35 |
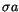 ; ;
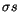 ; ;
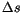 |
|
| 1993QN |
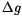 |
|
| 1993UT |
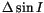 ; ;
 ; ;
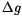 |
|
| 1993VV7 |
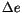 ; ;
 ; ;
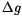 |
|
| 1994TA1 |
 ; ;
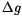 |
|
| 1995SU32 |
 ; ;
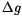 |
|
| 1998QX |
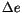 ; ;
 |
|
| 2705P-L |
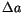 |
|
| 3230T-2 |
 |
2/1 |
For a comparison we show a similar table (Table 3) with the
``pathological'' data detected in 10 Myr runs. Here we have chosen to
include only asteroids for which one or more of the proper elements
had standard deviation in excess of the adopted threshold. In the
final output there are additional 20 objects with ``pathological''
standard deviations in frequencies, 9 objects with maximum excursion
in frequency above the critical value, and 73 objects for which the
maximum excursions of elements were found to be above the adopted
threshold.
Table 3:
The same as Table 2, but for the 10 Myr integration. Included
are only objects with excessive standard deviations of proper
elements.
| Asteroid |
Erroneous values |
Remark |
| 1301 |
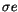 ; ;
 |
Pallas |
| 4177 |
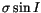 |
2:1 |
| 4997 |
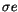 ; ;
 |
g=s; Pallas ? |
| 1979OA |
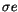 ; ;
 ; ;
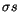 |
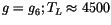 |
| 1981EJ40 |
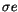 ; ;
 |
Pallas |
| 1991QG |
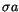 ; ;
 ; ;
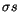 |
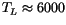 |
| 1993SQ3 |
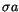 ; ;
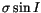 ; ;
 |
2:1 |
| 1993TC23 |
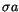 ; ;
 |
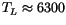 |
| 1993UT |
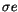 ; ;
 |
Pallas |
| 1995CT1 |
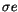 ; ;
 |
Pallas |
| 1996KL1 |
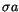 |
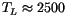 |
| 2705P-L |
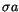 |
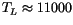 |
Not all of the asteroids with large standard deviations of proper
elements listed in Table 2 appear again in Table 3. For some cases,
namely 3480, 6626, and 1984 LK, this is because they went hyperbolic,
as discussed in Section 3.1. Many other bodies from Table
2 do not qualify for the ``pathological'' category in the
extended run because of the tighter definition (based on the RMS
only): e.g., the numbered asteroids 531, 3579, 4915, 5330, 7598.
However, there are indeed cases in which the standard deviation of the
proepr elements was improved in the longer integration: e.g. for
1993 FB35
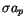 was improved. The running boxes of the 10 Myr
integration being 2 Myr, twice as long as the ones of the shorter
integration, the decrease of the instability of some proper element
indicates that averaging over an extended time span better removes
some long periodic perturbation.
Overall, however, we found more ``pathological'' cases in the long run
than in the short run. This could be expected since the deterioration
occurred for some chaotic asteroids and for a number of asteroids near
secular resonances. Thus in the long run the perturbation builds up
more effectively; this happens more often for large eccentricities
and/or inclination. As an example, a number of members of the high
inclination Pallas family originally discovered by Lemaitre and
Morbidelli ([1994]) appear in our Table 3. As a by-product
of our analysis, we have identified 12 new potential members of this
family: 5222, 5234, 8009, 1977 RD, 1981 EJ40, 1993 UT, 1993 VV7,
1994 PP, 1994 TA1, 1995 CT1, 1998 QX, 1998 QZ85. However, this is
possibly not a complete list, also because a number of high
eccentricity objects have been a-priori eliminated from our
integrations due to the osculating perihelion distance criterion
(Section 1).
It is obvious that some dynamical features (e.g. mean motion and
secular resonances) limiting the accuracy of the analytical theories
correspond to real effects in the exact dynamics, and therefore have
to appear also in the numerical integration output. Thus the derived
elements are as good as they can be, given that the definition of
proper elements must be uniform to satisfy the basic requirements of
the family identification procedures. Our synthetic theory makes use
of the averaging principle, which is well known not to work for
resonant asteroids. As a typical example of the outcome of an
inappropriate application of averaging, and of the ``erroneous''
definition of a proper element, let us mention the Griqua group of
asteroids, located in the 2:1 mean motion resonance with Jupiter. As
can be seen in Figures 7 and 8
(Section 3.4), all these bodies appear at the libration
center, that is, as if they all had the same proper semimajor axis of
was improved. The running boxes of the 10 Myr
integration being 2 Myr, twice as long as the ones of the shorter
integration, the decrease of the instability of some proper element
indicates that averaging over an extended time span better removes
some long periodic perturbation.
Overall, however, we found more ``pathological'' cases in the long run
than in the short run. This could be expected since the deterioration
occurred for some chaotic asteroids and for a number of asteroids near
secular resonances. Thus in the long run the perturbation builds up
more effectively; this happens more often for large eccentricities
and/or inclination. As an example, a number of members of the high
inclination Pallas family originally discovered by Lemaitre and
Morbidelli ([1994]) appear in our Table 3. As a by-product
of our analysis, we have identified 12 new potential members of this
family: 5222, 5234, 8009, 1977 RD, 1981 EJ40, 1993 UT, 1993 VV7,
1994 PP, 1994 TA1, 1995 CT1, 1998 QX, 1998 QZ85. However, this is
possibly not a complete list, also because a number of high
eccentricity objects have been a-priori eliminated from our
integrations due to the osculating perihelion distance criterion
(Section 1).
It is obvious that some dynamical features (e.g. mean motion and
secular resonances) limiting the accuracy of the analytical theories
correspond to real effects in the exact dynamics, and therefore have
to appear also in the numerical integration output. Thus the derived
elements are as good as they can be, given that the definition of
proper elements must be uniform to satisfy the basic requirements of
the family identification procedures. Our synthetic theory makes use
of the averaging principle, which is well known not to work for
resonant asteroids. As a typical example of the outcome of an
inappropriate application of averaging, and of the ``erroneous''
definition of a proper element, let us mention the Griqua group of
asteroids, located in the 2:1 mean motion resonance with Jupiter. As
can be seen in Figures 7 and 8
(Section 3.4), all these bodies appear at the libration
center, that is, as if they all had the same proper semimajor axis of
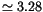 AU. Thus, even if these bodies are kept in the files,
one should not use these averaged semimajor axes for family
identification purposes.
A well-known solution to the problem of resonant asteroids is to adopt
some other proper value, taking into account the resonance in its very
definition, instead of the usual one. For example, the libration
amplitude of the semimajor axis could replace the averaged semimajor
axis (see, e.g., Milani [1993]), but then the question is how to
use different proper elements (of presumably different accuracy) in
the family identification procedure. Even if the bodies are only close
to strong resonances the accuracy of the determination of proper
elements is degraded and the same problem applies (see Milani and
Knezevic [1999], for an attempt to improve upon this
situation). Another approach is to compute special ``resonant proper
elements'' (Morbidelli et al. [1995]), but these do not belong
to the same 3D-space; such proper elements can be very useful locally
(to study dynamics), but cannot be used for large scale structures
(e.g., to identify families) because of the discontinuities and/or
topological changes. Let us just mention here that we shall later
(Section 3.5) revisit the problem of resonant asteroids,
to discuss the leakage of asteroid families members due to chaotic
diffusion along the resonances.
There are other reasons why synthetic proper elements and frequencies
have been poorly determined in some special cases. For asteroids with
very low eccentricities and high inclinations (
AU. Thus, even if these bodies are kept in the files,
one should not use these averaged semimajor axes for family
identification purposes.
A well-known solution to the problem of resonant asteroids is to adopt
some other proper value, taking into account the resonance in its very
definition, instead of the usual one. For example, the libration
amplitude of the semimajor axis could replace the averaged semimajor
axis (see, e.g., Milani [1993]), but then the question is how to
use different proper elements (of presumably different accuracy) in
the family identification procedure. Even if the bodies are only close
to strong resonances the accuracy of the determination of proper
elements is degraded and the same problem applies (see Milani and
Knezevic [1999], for an attempt to improve upon this
situation). Another approach is to compute special ``resonant proper
elements'' (Morbidelli et al. [1995]), but these do not belong
to the same 3D-space; such proper elements can be very useful locally
(to study dynamics), but cannot be used for large scale structures
(e.g., to identify families) because of the discontinuities and/or
topological changes. Let us just mention here that we shall later
(Section 3.5) revisit the problem of resonant asteroids,
to discuss the leakage of asteroid families members due to chaotic
diffusion along the resonances.
There are other reasons why synthetic proper elements and frequencies
have been poorly determined in some special cases. For asteroids with
very low eccentricities and high inclinations (
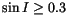 )
two
problems simultaneously affect the computation of proper elements. In
the real dynamics, strong secular resonances (with frequencies either
g-g5, g-g6, g-g7 or 2g-2s near zero) affect the
determination of the proper values. At the same time the argument of
the proper mode may be difficult to compute from the time series
(k(t),h(t)) because the point (k,h) may sometimes be too close to
zero. Both effects combine in an inaccurate computation of the proper
frequency g; the proper value ep is nevertheless accurate. For
example, this appears to be the case with the asteroid 1991 UC, which
has so low proper eccentricity (
ep=0.0031) that an automatic
computation of the proper longitude of perihelion was not
possible. However, we have not performed any ``manual intervention''
in such cases, both because it would necessarily introduce subjective
choices in the very definition of proper elements, and because it
would make our procedure impossible to use in the context of an
automated information services such as AstDyS (and the companion
information system NEODyS http://newton.dm.unipi.it/neodys/).
Some other cases of inaccurate computations of proper elements and/or
Lyapunov exponents are the result of very chaotic motion and
macroscopic instabilities. In few such cases this forced us to
manually correct some wild results. As an example, for the asteroid
1991 QG an output format overflow occurred in the 10 Myr integration
for the maximum excursions of the nodal frequency and of the mean
longitude residuals with respect to the linear fit (we simply set
these two values to zero keeping the rest of the data). Note that the
semimajor axis of this asteroid was very poorly determined even in the
short run (Table 2), and that it became even worse in the extended
one: we are dealing with a strongly chaotic object (Lyapunov time on
the order of few thousand years), and such wild oscillations are not
surprising.
)
two
problems simultaneously affect the computation of proper elements. In
the real dynamics, strong secular resonances (with frequencies either
g-g5, g-g6, g-g7 or 2g-2s near zero) affect the
determination of the proper values. At the same time the argument of
the proper mode may be difficult to compute from the time series
(k(t),h(t)) because the point (k,h) may sometimes be too close to
zero. Both effects combine in an inaccurate computation of the proper
frequency g; the proper value ep is nevertheless accurate. For
example, this appears to be the case with the asteroid 1991 UC, which
has so low proper eccentricity (
ep=0.0031) that an automatic
computation of the proper longitude of perihelion was not
possible. However, we have not performed any ``manual intervention''
in such cases, both because it would necessarily introduce subjective
choices in the very definition of proper elements, and because it
would make our procedure impossible to use in the context of an
automated information services such as AstDyS (and the companion
information system NEODyS http://newton.dm.unipi.it/neodys/).
Some other cases of inaccurate computations of proper elements and/or
Lyapunov exponents are the result of very chaotic motion and
macroscopic instabilities. In few such cases this forced us to
manually correct some wild results. As an example, for the asteroid
1991 QG an output format overflow occurred in the 10 Myr integration
for the maximum excursions of the nodal frequency and of the mean
longitude residuals with respect to the linear fit (we simply set
these two values to zero keeping the rest of the data). Note that the
semimajor axis of this asteroid was very poorly determined even in the
short run (Table 2), and that it became even worse in the extended
one: we are dealing with a strongly chaotic object (Lyapunov time on
the order of few thousand years), and such wild oscillations are not
surprising.



Next: 3.3 Stability
Up: 3. Results
Previous: 3.1 Hyperbolic cases
Andrea Milani
2000-10-03