


Next: 3.5 Families
Up: 3. Results
Previous: 3.3 Stability
3.4 Global view of the outer main belt
A global view of the outer main asteroid belt is given on
Figures 7 and 8 in the (a,e) and
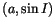 planes, respectively. Only asteroids with good proper
elements are shown on these plots (the actual criteria were exactly
opposite from those for the inclusion in the 10 Myr run, that is
planes, respectively. Only asteroids with good proper
elements are shown on these plots (the actual criteria were exactly
opposite from those for the inclusion in the 10 Myr run, that is
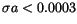 ,
,
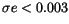 ,
,
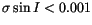 and
and
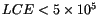 ). The plots are made with the data from the joint
catalog.
). The plots are made with the data from the joint
catalog.
Figure:
An overview of the asteroid outer main belt in proper
semimajor axis vs. proper eccentricity plane. Only asteroids with
accurately determined proper elements are shown.
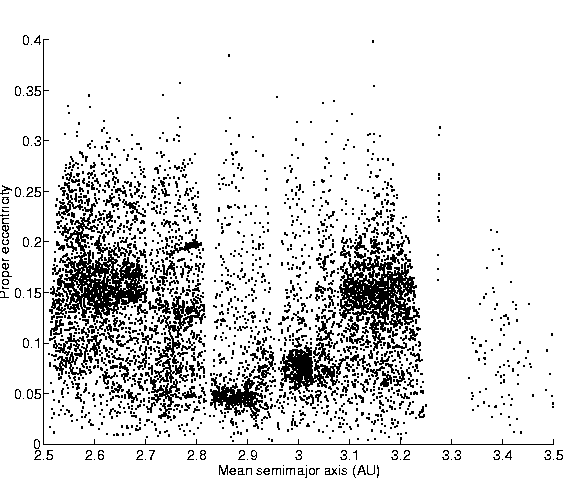 |
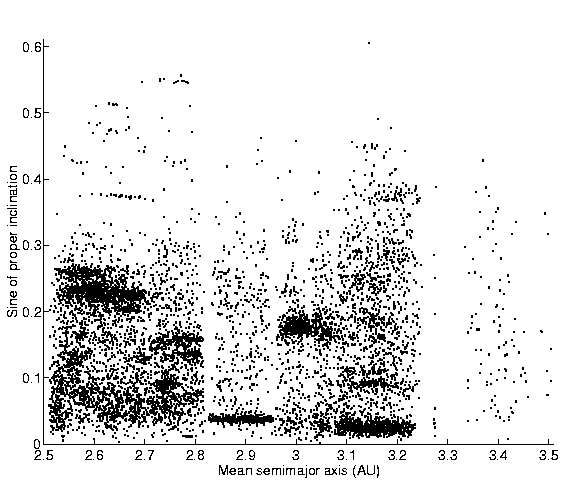
A prominent feature in Figure 8 is a ``line'' of
objects at proper inclination
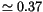 and with
2.6<ap<2.7
AU. These objects all have a low proper eccentricity, but only for a
subset the values of ep are in a narrow range, indicating a
possible Hansa family (from 480 Hansa, the lowest numbered asteroid in
this group); such a Hansa family had already been proposed by
Hergenrother et al. ([1996]) and studied by A. Lemaitre
by means of semianalytic proper elements (A. Lemaitre, personal
communication). It is likely that such a family exists, that is, that
these asteroids are collisionally related; however, without a detailed
study we cannot exclude that such grouping is only apparent, due to an
island of stability surrounded by secular resonances.
and with
2.6<ap<2.7
AU. These objects all have a low proper eccentricity, but only for a
subset the values of ep are in a narrow range, indicating a
possible Hansa family (from 480 Hansa, the lowest numbered asteroid in
this group); such a Hansa family had already been proposed by
Hergenrother et al. ([1996]) and studied by A. Lemaitre
by means of semianalytic proper elements (A. Lemaitre, personal
communication). It is likely that such a family exists, that is, that
these asteroids are collisionally related; however, without a detailed
study we cannot exclude that such grouping is only apparent, due to an
island of stability surrounded by secular resonances.
Figure:
An overview of the asteroid outer main belt in proper
semimajor axis vs. sine of proper inclination plane. Only asteroids
with accurately determined proper elements are shown.
 |
In Figure 9 the troublesome cases are shown in
the same planes (ap,ep) and
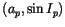 .
The chaotic
asteroids (either
.
The chaotic
asteroids (either
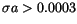 or
or
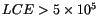 )
are
shown on the left: these two plots illustrate again the fact that the
mean motion resonances are the main source of chaotic behavior for
main belt asteroids. The chaotic objects are distributed along
numerous easily recognizable resonant strips; chaotic diffusion takes
place along the resonance lines (see Section 3.5). The
most affected region is between 3.0 and 3.2 AU, even if in that region
there are also many fairly stable asteroids (see
Figures 7 and 8) and the region does not
appear to be a continuous chaotic sea.
On the right of Figure 9 we show the orbits affected by
the secular resonances (either
)
are
shown on the left: these two plots illustrate again the fact that the
mean motion resonances are the main source of chaotic behavior for
main belt asteroids. The chaotic objects are distributed along
numerous easily recognizable resonant strips; chaotic diffusion takes
place along the resonance lines (see Section 3.5). The
most affected region is between 3.0 and 3.2 AU, even if in that region
there are also many fairly stable asteroids (see
Figures 7 and 8) and the region does not
appear to be a continuous chaotic sea.
On the right of Figure 9 we show the orbits affected by
the secular resonances (either
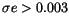 or
or
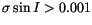 ). These two plots illustrate the effects of secular resonances,
the most prominent feature being the outline of a group of overlapping
nonlinear secular resonances between 2.5 and 2.8 AU, at low to
moderate inclination and eccentricity. The location of these
resonances as revealed by the numerical integration coincides with the
analytical prediction (see Figures 7-11 in Milani and Knezevic
[1994]). The numerical output not only indicates the exact
location of these resonances, but can be used to estimate their width,
providing in the same time a clear indication of the level of
degradation of the proper elements due to the resonances themselves.
). These two plots illustrate the effects of secular resonances,
the most prominent feature being the outline of a group of overlapping
nonlinear secular resonances between 2.5 and 2.8 AU, at low to
moderate inclination and eccentricity. The location of these
resonances as revealed by the numerical integration coincides with the
analytical prediction (see Figures 7-11 in Milani and Knezevic
[1994]). The numerical output not only indicates the exact
location of these resonances, but can be used to estimate their width,
providing in the same time a clear indication of the level of
degradation of the proper elements due to the resonances themselves.
Figure:
A composite figure showing chaotic asteroids
(left) and asteroids with large standard deviations of
eccentricity/inclination, affected by the secular resonances in the
zone between 2.5 and 2.8 AU (right) in the proper semimajor axis
vs. eccentricity (up), and semimajor axis vs. sine of inclination
(bottom) plane.
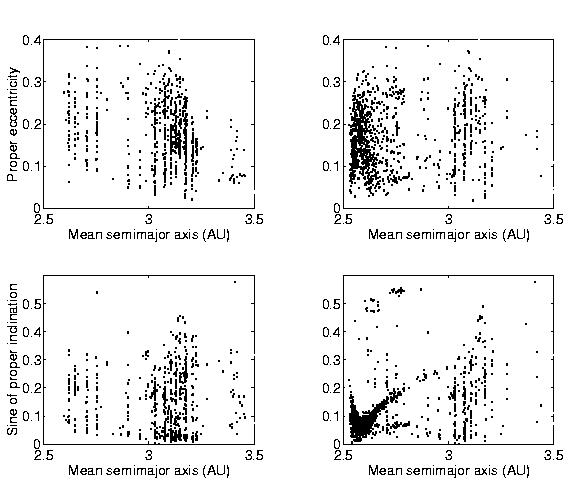 |
The comparison of the plots presented on Figure 9, which
has been prepared with the composite catalog, with the analoguous
plots produced with the data from the 2 yr run, shows an additional
feature. Quite a number of objects found to be chaotic in the short
run and thus appearing on the plots on the left, appear also on the
other pair of plots on the right in the long run, even if the objects
are not close to any significant secular resonance. As discussed
above, chaotic perturbations affect immediately the semimajor axis,
but on the long run chaotic diffusion also affects the other proper
variables.



Next: 3.5 Families
Up: 3. Results
Previous: 3.3 Stability
Andrea Milani
2000-10-03



