


Next: 2. Synthetic theory
Up: Synthetic proper elementsfor outer
Previous: Synthetic proper elementsfor outer
1. Introduction
The main motivation to produce ``yet another set of asteroid proper
elements'' is that for many asteroids the currently available proper
elements, derived by means of an analytical theory by Milani and Knezevic ([1990,1992,1994]), are not (any more)
accurate enough, at least when these elements are used to identify
and study asteroid dynamical families, and to try to understand the
dynamical structure of the asteroid belt.
In the densely populated low to moderate eccentricity and inclination
region of the asteroid main belt, the proper elements computed
analytically are accurate to a level very close to the best result
achievable by any analytical theory (Milani and Knezevic
[1994]). This because there is an infinite web of resonances
(Arnold [1963]), and because of the occurrence of chaotic
motions. It is not yet clear whether the asteroid belt is a big
chaotic sea (although with diffusion times on the order of billions of
years), or it is structured in the sense described by Nekoroshev
theorem for quasi-integrable Hamiltonian systems (Morbidelli and Guzzo
[1997]). However, it is now established that the motions of
asteroids are basically chaotic, and that only the dynamical
mechanisms responsible for this chaos, the time scales involved, and
the size and form of the resulting macroscopic instabilities are
different (Milani et al. [1997]). Moreover, asteroids are not
allowed to be less chaotic than the perturbing major planets (Laskar
[1989], Nobili et al. [1989]), and this ``induced
chaos'' introduces a chaotic noise in the asteroid proper elements of
the order of 10-4 (Milani and Knezevic [1994]).
The typical instability of the current analytical proper elements in
proper e and sin I is
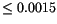 over 5 Myr (Milani and Knezevic [1994]). This accuracy was enough for Zappalà et
al. ([1995]) to reliably identify asteroid families in a
sample of 12,487 asteroids and throughout almost the entire belt.
However, they also found that there are still some regions of the belt
where a reliable identification of families was not possible. This
could result from two main problems: either the proper elements in
these regions were of degraded accuracy (e.g. near the resonances; see
Milani and Knezevic [1999] for an attempt to improve
upon the accuracy of mean/proper elements of asteroids in the vicinity
of the mean motion resonances), or the background density of asteroids
was too high, thus smearing the family borders and forcing the
clumping of families which should have been kept separate (this
applies especially in the Flora region).
In addition, it has been recently recognized that chaotic diffusion,
acting over very long time spans, can drive members of the families
out of the regions in the phase space occupied by the families. Such a
diffusive transport of the bodies seems to be common if a family is
cut through by some mean motion resonances, giving rise to chaotic
behavior localized to a narrow range of semiamjor axis (Milani and
Farinella [1994], Milani et al. [1997], Morbidelli
and Nesvorný [1999]). Another efficient mechanism of
``family erosion'' is provided by the Yarkovsky effect, which also
appears to transport some family members out of the families by
pushing them into the nearby resonances (Vokrouhlichký et
al. [1999]).
In an attempt to solve the problem, and to produce proper elements
more accurate, more stable in time and more reliable, we have tried a
different method to compute asteroid proper elements. We adopted an
approach similar to the one used for the major outer planets by
Carpino et al. ([1987]): by purely numerical techniques, we
produced so-called ``synthetic'' proper elements for a large sample of
asteroids. The procedure consists of simultaneous integration of the
asteroid orbits for a ``long-enough'' time span, online filtering of
the short-periodic perturbations and computation of Lyapunov
Characteristic Exponents to monitor the chaotic behaviors. The output
of the integration is then spectrally resolved under constraints set
by d'Alembert rules, and the principal harmonics (proper values)
extracted from the time series, together with the associated
fundamental frequencies.
It is quite obvious that with such an approach we have to handle in
different ways the inner and the outer part of the main belt. In the
outer part of the belt we are allowed to use a somewhat simplified
dynamical model: the direct perturbation are included only for the
four outer major planets, while a barycentric correction applied to
the initial conditions removes most indirect effects of the inner
planets (Milani and Knezevic [1992]). In this way we
could speed up the numerical integrations by choosing a longer step
size. In the inner part of the main belt, on the other hand, we have
to include the effects of the terrestrial planets (at least Mars and
Earth), and this makes the model more complex and significantly slows
down the integration.
In this paper we present the results of the first phase of this work,
that is the results of computation of the synthetic proper elements
for a total of 10,265 asteroids located in the outer main belt,
between 2.5 AU and 4.0 AU. We propagated all the orbits for 2 Myr, but
in a number of troublesome cases we extended the integrations to
10 Myr. We have included in this catalog only numbered and
multi-opposition objects, to be sure that their osculating orbital
elements are accurate enough; there would be no point in producing
proper elements with a computational accuracy better than the one of
the available osculating elements. We have also excluded the high
eccentricity Mars approachers, that is those with initial perihelion
q<1.75 AU, because for these the perturbations by Mars should be
taken into account.
The rest of the paper is organized as follows. In
Section 2 we explain what is a synthetic theory,
describe the procedures involved, the input data, and other important
details and technicalities; in Section 3. we present and discuss
the results, with special emphasis on the hyperbolic, resonant and
chaotic cases, and we asses the accuracy and stability of the
synthetic proper elements we have computed. We also give some examples
of the new features, of the dynamical structure of the entire belt and
of some families, which are made visible by more accurate and reliable
proper elements. Finally, in Section 4 we summarize the results,
draw some conclusions, and discuss future work.
over 5 Myr (Milani and Knezevic [1994]). This accuracy was enough for Zappalà et
al. ([1995]) to reliably identify asteroid families in a
sample of 12,487 asteroids and throughout almost the entire belt.
However, they also found that there are still some regions of the belt
where a reliable identification of families was not possible. This
could result from two main problems: either the proper elements in
these regions were of degraded accuracy (e.g. near the resonances; see
Milani and Knezevic [1999] for an attempt to improve
upon the accuracy of mean/proper elements of asteroids in the vicinity
of the mean motion resonances), or the background density of asteroids
was too high, thus smearing the family borders and forcing the
clumping of families which should have been kept separate (this
applies especially in the Flora region).
In addition, it has been recently recognized that chaotic diffusion,
acting over very long time spans, can drive members of the families
out of the regions in the phase space occupied by the families. Such a
diffusive transport of the bodies seems to be common if a family is
cut through by some mean motion resonances, giving rise to chaotic
behavior localized to a narrow range of semiamjor axis (Milani and
Farinella [1994], Milani et al. [1997], Morbidelli
and Nesvorný [1999]). Another efficient mechanism of
``family erosion'' is provided by the Yarkovsky effect, which also
appears to transport some family members out of the families by
pushing them into the nearby resonances (Vokrouhlichký et
al. [1999]).
In an attempt to solve the problem, and to produce proper elements
more accurate, more stable in time and more reliable, we have tried a
different method to compute asteroid proper elements. We adopted an
approach similar to the one used for the major outer planets by
Carpino et al. ([1987]): by purely numerical techniques, we
produced so-called ``synthetic'' proper elements for a large sample of
asteroids. The procedure consists of simultaneous integration of the
asteroid orbits for a ``long-enough'' time span, online filtering of
the short-periodic perturbations and computation of Lyapunov
Characteristic Exponents to monitor the chaotic behaviors. The output
of the integration is then spectrally resolved under constraints set
by d'Alembert rules, and the principal harmonics (proper values)
extracted from the time series, together with the associated
fundamental frequencies.
It is quite obvious that with such an approach we have to handle in
different ways the inner and the outer part of the main belt. In the
outer part of the belt we are allowed to use a somewhat simplified
dynamical model: the direct perturbation are included only for the
four outer major planets, while a barycentric correction applied to
the initial conditions removes most indirect effects of the inner
planets (Milani and Knezevic [1992]). In this way we
could speed up the numerical integrations by choosing a longer step
size. In the inner part of the main belt, on the other hand, we have
to include the effects of the terrestrial planets (at least Mars and
Earth), and this makes the model more complex and significantly slows
down the integration.
In this paper we present the results of the first phase of this work,
that is the results of computation of the synthetic proper elements
for a total of 10,265 asteroids located in the outer main belt,
between 2.5 AU and 4.0 AU. We propagated all the orbits for 2 Myr, but
in a number of troublesome cases we extended the integrations to
10 Myr. We have included in this catalog only numbered and
multi-opposition objects, to be sure that their osculating orbital
elements are accurate enough; there would be no point in producing
proper elements with a computational accuracy better than the one of
the available osculating elements. We have also excluded the high
eccentricity Mars approachers, that is those with initial perihelion
q<1.75 AU, because for these the perturbations by Mars should be
taken into account.
The rest of the paper is organized as follows. In
Section 2 we explain what is a synthetic theory,
describe the procedures involved, the input data, and other important
details and technicalities; in Section 3. we present and discuss
the results, with special emphasis on the hyperbolic, resonant and
chaotic cases, and we asses the accuracy and stability of the
synthetic proper elements we have computed. We also give some examples
of the new features, of the dynamical structure of the entire belt and
of some families, which are made visible by more accurate and reliable
proper elements. Finally, in Section 4 we summarize the results,
draw some conclusions, and discuss future work.



Next: 2. Synthetic theory
Up: Synthetic proper elementsfor outer
Previous: Synthetic proper elementsfor outer
Andrea Milani
2000-10-03