


Next: 3.2 Resonant and ``pathological''
Up: 3. Results
Previous: 3. Results
3.1 Hyperbolic cases
Let us begin with the most unstable orbits, that is with those that
already during the 2 Myr integration became hyperbolic (see Table 1,
upper part). For these 9 escaping asteroids it was not possible to
determine synthetic proper elements, and they are removed from the
output files. 14 additional bodies became hyperbolic in the extended
10 Myr integration (Table 1, lower part). For the sake of
completeness, for these bodies udergoing hyperbolic escape within
10 Myr we have included in the output files the synthetic proper
elements derived from the 2 Myr integrations, even if these values are
highly unreliable and should be considered with extreme caution. In
few cases (3480, 1998 OP12) the computation of the LCE failed because
of overflow, due to too long interval between renormalizations; the
LCE value has been set to zero manually. Note that we thus provide
proper elements for a total of 10,256 asteroids.
Table 1:
Upper part: asteroids that became hyperbolic in the 2 Myr
integration. Lower part: additional bodies that escaped during the
extended 10 Myr integration. Columns contain asteroid identifier,
semimajor axis, eccentricity and inclination at the beginning of the
integration, and comment on the relevant dynamical features that might
give rise to chaotic diffusion. TL denotes the Lyapunov time in
years.
| Asteroid |
a0 (AU) |
e0 |
I0 (deg) |
Remark |
| 1921 |
3.263 |
0.402 |
19.45 |
2/1 |
| 5164 |
3.643 |
0.504 |
19.84 |
outer belt |
| 7458 |
3.830 |
0.137 |
1.81 |
outer belt |
| 8119 |
2.963 |
0.166 |
0.61 |
7/3 |
| 1988DX1 |
2.828 |
0.175 |
8.13 |
5/2 |
| 1989TT3 |
2.820 |
0.157 |
3.00 |
5/2 |
| 1993SG13 |
2.958 |
0.228 |
6.85 |
7/3 |
| 1993TC14 |
3.304 |
0.273 |
0.35 |
2/1 |
| 2202T-1 |
3.122 |
0.329 |
4.14 |
2/1 ? |
| |
|
|
|
|
| |
|
|
|
|
| 677 |
2.962 |
0.044 |
8.47 |
7/3
TL = 6060 yr |
| 2658 |
3.076 |
0.290 |
9.32 |
|
| 3480 |
3.045 |
0.283 |
3.76 |
|
| 6626 |
3.025 |
0.388 |
2.12 |
9/4 |
| 7410 |
3.022 |
0.376 |
5.85 |
9/4 |
| 8560 |
2.959 |
0.068 |
13.38 |
7/3
TL = 6200 yr |
| 1984LK |
3.115 |
0.386 |
6.55 |
2/1 ? |
| 1990OB2 |
3.035 |
0.335 |
11.68 |
|
| 1991WB |
2.747 |
0.330 |
35.99 |
secular res. |
| 1996EJ14 |
3.029 |
0.096 |
15.80 |
9/4 |
| 1998DD2 |
3.058 |
0.318 |
8.35 |
|
| 1998KY30 |
3.203 |
0.190 |
14.29 |
2:1
TL = 6200 yr |
| 1998OP12 |
3.038 |
0.307 |
1.31 |
|
| 1998QO47 |
3.085 |
0.340 |
6.17 |
|
We have not performed a detailed analysis of the reasons for such
extreme instability. However, as it can be seen from the Remark column
in Table 1, most of these orbits are from the start either inside or
very close to some low order mean motion resonances, such as 2/1,
5/2, 7/3 and 9/4. Most of the others have a large initial
eccentricity, the only exception being one case in the most unstable
portion of the outer belt, with
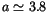 AU.
This leakage we found from the main belt to hyperbolic orbits, due to
gravitational perturbations only, can be extrapolated to get an
estimate of the total loss over the age of the Solar System. If we
extrapolate linearly from 9 bodies lost in 2 Myr, we could have as
much as 20,000 bodies lost over 4.5 Gyr. If we extrapolate from the
10 Myr integration, with 23 orbits going hyperbolic, that is
AU.
This leakage we found from the main belt to hyperbolic orbits, due to
gravitational perturbations only, can be extrapolated to get an
estimate of the total loss over the age of the Solar System. If we
extrapolate linearly from 9 bodies lost in 2 Myr, we could have as
much as 20,000 bodies lost over 4.5 Gyr. If we extrapolate from the
10 Myr integration, with 23 orbits going hyperbolic, that is 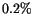 of the considered sample, we could have
of the considered sample, we could have
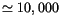 lost over the
age of the solar system. Even if this oversimplified computation does
not take into account the size of the original population, its
collisional evolution, non gravitational perturbations, nor any other
refinement, it clearly demonstrates that this is by no means a
negligible phenomenon, and that the original number of asteroids must
have been significantly larger than the present one.
lost over the
age of the solar system. Even if this oversimplified computation does
not take into account the size of the original population, its
collisional evolution, non gravitational perturbations, nor any other
refinement, it clearly demonstrates that this is by no means a
negligible phenomenon, and that the original number of asteroids must
have been significantly larger than the present one.



Next: 3.2 Resonant and ``pathological''
Up: 3. Results
Previous: 3. Results
Andrea Milani
2000-10-03