B.2 COMPITO PARZIALE 20 Dicembre 2001

Esercizio Sia dato il sistema dinamico newtoniano ad un grado di libertà:

$$\frac{d^2{x}}{d{t}^2}=-4x^3+2x-\gamma\, \frac{d{x}}{d{t}}$$

con dissipazione $1>\gamma>0$, le cui soluzioni nel piano $(x,\dot x)$ sono come nella Figura 3.11.

a) Discretizzare il sistema dinamico continuo con passo $h>0$, ottenendo un'equazione alle differenze finite del secondo ordine, con le approssimazioni:

$$\ddot x\simeq \frac{\Delta_0^2x}{h^2} \ \ \ ; \ \ \ \dot x \simeq \frac{\Delta_-x}h \ .$$

Trasformare l'equazione alle differenze finite del secondo ordine in un sistema dinamico discreto:

$$\left[\begin{array}{c}{x_{k+1}}\\ {y_{k+1}}\end{array}\rig... ... \rm con} \ \ y_k=\frac {x_k-x_{k-1}}h=\frac{\Delta_-x_k}h \ .$$

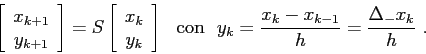
b) Trovare i punti fissi $S(x,y)=(x,y)$.

c) Calcolare la matrice jacobiana

$$D S (x_k,y_k)= \frac{\partial (x_{k+1}, y_{k+1})}{\partial (x_k, y_k)}$$

e provare che il punto fisso corrispondente alla sella del sistema dinamico continuo è sempre iperbolico. (Suggerimento: calcolare il polinomio caratteristico in $0$ e in $1$.)

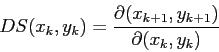
d) Provare che i punti fissi corrispondenti ai fuochi del sistema dinamico continuo sono asintoticamente stabili. (Suggerimento: come sopra.) (Soluzione)

Esercizio Si consideri il problema del moto di un pendolo di massa $m$ e lunghezza $\ell$ in un piano verticale che viene fatto ruotare con velocità angolare costante $\Omega$ attorno ad un asse verticale passante per il punto di sospensione del pendolo (vedi figura), e soggetto ad un'accelerazione di gravità costante verso il basso e di intensità $g$. .

Figura B.1: L'angolo $\theta$ formato dal pendolo con la verticale si può usare come coordinata.

a) Scrivere la Lagrangiana del sistema e le equazioni di Lagrange.

b) Calcolare la trasformazione di Legendre, scrivere la funzione Hamiltoniana (in funzione del momento $p$ e della coordinata $\theta$) e le equazioni di Hamilton.

c) Trovare i punti di equilibrio e studiarne la stabilità, in funzione del parametro $g/\Omega^2\,\ell$.

d) Tracciare un grafico qualitativo delle soluzioni (o nel piano $(\theta, \dot\theta)$ o in quello $(p, \theta)$), a seconda del valore del parametro.

e) La funzione Hamiltoniana è l'energia del sistema? Se no, calcolare la potenza del motore che fa girare il pendolo.

(Soluzione)