B.3 COMPITO D'ESAME 14 Gennaio 2002

Esercizio Dato il sistema dinamico continuo lineare in ${\cal R}^2$:

$$\frac{d{X}}{d{t}}= \left[\begin{array}{cc}{2}&{-1}\\ {1}&{\phantom{-}0}\end{array}\right] \; X$$

a) scrivere esplicitamente tutte le orbite in funzione delle condizioni iniziali;

b) trovare quali condizioni iniziali danno luogo ad orbite con l'origine come limite per $t\to -\infty$.

(Soluzione)

Esercizio Sia dato il sistema dinamico newtoniano ad un grado di libertà:

$$\ddot x=-3x^2+1$$

le cui soluzioni nel hanno l'andamento descritto dalla Figura B.2.

Figura B.2: Sopra: La funzione energia potenziale $V(x)$. Sotto: curve di livello dell'energia, corrispondenti ai livelli segnati nella figura sopra.

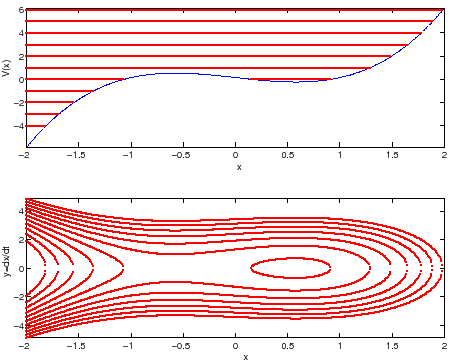a) Discretizzare il sistema dinamico continuo con passo $h>0$, ottenendo un'equazione alle differenze finite del secondo ordine, con l' approssimazione: $\ddot x\simeq {\Delta_0^2x}/{h^2}$. Trasformare l'equazione alle differenze finite del secondo ordine in un sistema dinamico discreto:

$$\left[\begin{array}{c}{x_{k+1}}\\ {y_{k+1}}\end{array}\rig... ... \rm con} \ \ y_k=\frac {x_k-x_{k-1}}h=\frac{\Delta_-x_k}h \ .$$

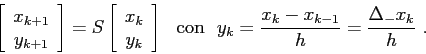
b) Trovare i punti fissi $S(x,y)=(x,y)$.

c) Calcolare la matrice jacobiana $D S (x_k,y_k)= \partial (x_{k+1}, y_{k+1})/{\partial (x_k, y_k)}$ e provare che il punto fisso corrispondente alla sella del sistema dinamico continuo è sempre iperbolico.

d) Per quali valori di $h$ il punto corrispondente al punto di equlibrio con linearizzato di tipo centro è un punto fisso ellittico?

(Soluzione)

Esercizio Un asta di massa trascurabile e lunghezza $\ell$ si muove (senza attrito) tenendo sempre un estremo sull'asse orizzontale $x$ ed un estremo sull'asse verticale $z$. All'asta è attaccato un punto materiale di massa $M$, in modo che la sua distanza dall'estremo sull'asse $z$ è $k\,\ell$, con $0<k<1$. Il punto materiale è anche soggetto ad una accelerazione di gravità, rivolta nel verso negativo dell'asse $z$ e di intensità fissa $g$.

a) Parametrizzare con il moto del punto materiale, usando come parametro l'angolo $\theta$ nel piano $(x,z)$ tra l'asse $z$ (nel senso delle $z$ negative) e l'asta (si veda la Figura B.3).

Figura B.3: Asta con estremi che possono scorrere sugli assi.

b) Scrivere l'energia cinetica e l'energia potenziale del punto materiale.

c) Scrivere la lagrangiana, la hamiltoniana e le equazioni di Hamilton del sistema.

d) Trovare i punti di equilibrio e discuterne la stabilità.

e) Si descriva qualitativamente il moto nel piano $(p, \theta)$ oppure $(\theta, \dot\theta)$.

f) Si trovi per quali valori della velocità angolare $\dot \theta$ una condizione iniziale $(\theta=\pi,\dot\theta)$ porta ad una circolazione, cioè con $\theta(t)$ una funzione monotona (crescente o decrescente). (Soluzione)