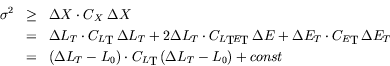Next: 2.5 Preimage of the
Up: 2. Computational methods
Previous: 2.3 Target plane analysis
2.4 Finding virtual impactors
Around some times ti many of the virtual asteroids Xi experience
a close approach to the Earth; this we call a virtual shower. A
shower can be decomposed into separate returns, which are
continuous strings of solutions having the same close approach; they
are represented by sequences of n consecutive solutions
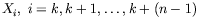 .
It is often the case that the shower at a
given time contains several different returns [Milani et al. 1999, Table 1].
For each return we want to identify the closest possible approach in
order to decide if an impact is possible. Starting from the solution
Xj that has the closest approach among the ones of the return, we
apply corrections to it to push the approach towards a closer one; the
method is a variant of Newton's method, also called differential
corrections in the context of orbit determination. It is similar, but
not identical, to one method used in [Muinonen 1999].
.
It is often the case that the shower at a
given time contains several different returns [Milani et al. 1999, Table 1].
For each return we want to identify the closest possible approach in
order to decide if an impact is possible. Starting from the solution
Xj that has the closest approach among the ones of the return, we
apply corrections to it to push the approach towards a closer one; the
method is a variant of Newton's method, also called differential
corrections in the context of orbit determination. It is similar, but
not identical, to one method used in [Muinonen 1999].
We begin by defining the correction we would like to apply on the MTP,
which is
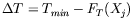 .
Then we need to identify a
change
.
Then we need to identify a
change 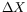 in the orbital elements (with respect to Xj),
such that
in the orbital elements (with respect to Xj),
such that
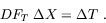 |
(2) |
To this purpose, we have to consider that DFT is a composition of a
projection
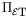 onto a two-dimensional subspace
onto a two-dimensional subspace
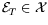 ,
followed by an invertible map
,
followed by an invertible map
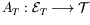 :
:
Here
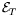 is the 2-dimensional subspace of
is the 2-dimensional subspace of 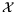 spanned
by the two rows of DFT. We further define
spanned
by the two rows of DFT. We further define
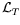 to be the
4-dimensional subspace of
to be the
4-dimensional subspace of 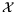 orthogonal to
orthogonal to
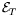 ,
so
that
,
so
that
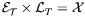 .
In simple terms, a change
in the orbital elements along
.
In simple terms, a change
in the orbital elements along
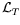 does not change the
position on the target plane, as far as the linear approximation is
applicable. It is possible to perform a change of coordinates in
does not change the
position on the target plane, as far as the linear approximation is
applicable. It is possible to perform a change of coordinates in
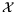 ,
by means of an orthogonal
,
by means of an orthogonal 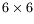 matrix V, in such
a way that
matrix V, in such
a way that
with
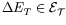 and
and
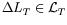 ;
then
the normal matrix CX in the new coordinate system is changed into
;
then
the normal matrix CX in the new coordinate system is changed into
in this way the contributions to Eq. (1) from the two
components can be identified.
On the contrary, all changes along
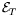 map linearly into
nonzero changes on the target plane; thus there is an inverse map
BT=AT-1. The projection
map linearly into
nonzero changes on the target plane; thus there is an inverse map
BT=AT-1. The projection
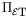 is not invertible,
the preimage of each point being a 4-dimensional space. However, we
can select one change in orbital elements
is not invertible,
the preimage of each point being a 4-dimensional space. However, we
can select one change in orbital elements
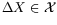 which
has a given displacement as image on the target plane
which
has a given displacement as image on the target plane
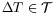 .
The portion of the preimage contained in the confidence
ellipsoid (1) can be described by the inequality
.
The portion of the preimage contained in the confidence
ellipsoid (1) can be described by the inequality
where
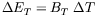 is fixed, uniquely determined by
the MTP displacement
is fixed, uniquely determined by
the MTP displacement 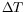 .
The above inequality, seen with
.
The above inequality, seen with
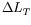 only as variable, defines a 4-dimensional ellipsoid (with
interior)
only as variable, defines a 4-dimensional ellipsoid (with
interior)
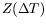 ;
we are going to select as representative of
;
we are going to select as representative of
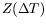 the point L0, which is the center of symmetry of this
ellipsoid. L0 can be computed in several different ways
[Milani 1999, Sec. 2], e.g., by separating the terms of different
degrees in
the point L0, which is the center of symmetry of this
ellipsoid. L0 can be computed in several different ways
[Milani 1999, Sec. 2], e.g., by separating the terms of different
degrees in 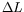 ,
and is obtained as a function of
,
and is obtained as a function of
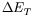 as
as
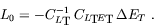 |
(3) |
This allows to select
![\begin{displaymath}\Delta X= V\;\left[\begin{array}{c}{\Delta E_T}\\
{-C_{L_T}...
...}\;C_{L_TE_T}}\end{array}\right]\;B_T\;\Delta T= H_T(\Delta T)
\end{displaymath}](img59.gif) |
(4) |
in such a way that (2) is satisfied. Then the orbit with
initial conditions
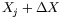 is propagated to the time
is propagated to the time
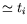 of
the close approach under study, and because of the nonlinear effects
of
the close approach under study, and because of the nonlinear effects
but the distance between the new MTP point and Tmin is now
smaller, and the procedure can be iterated. This means we reset the
`nominal' orbit to
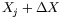 ,
we compute its MTP and its partial
derivatives matrix DFT, find a new weak direction, a new minimum
distance point Tmin along the weak direction, then select a new
,
we compute its MTP and its partial
derivatives matrix DFT, find a new weak direction, a new minimum
distance point Tmin along the weak direction, then select a new
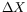 satisfying the new version of Eq. (2), and so on
until convergence. If the close approach distance at convergence is
less than one Earth radius, a virtual impactor has been found. If the
close approach distance at convergence of Newton's method is above one
Earth radius, but the width
satisfying the new version of Eq. (2), and so on
until convergence. If the close approach distance at convergence is
less than one Earth radius, a virtual impactor has been found. If the
close approach distance at convergence of Newton's method is above one
Earth radius, but the width
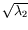 of the MTP ellipse is
such that impact is possible, a VI exists, although it is not on the
LOV.
of the MTP ellipse is
such that impact is possible, a VI exists, although it is not on the
LOV.



Next: 2.5 Preimage of the
Up: 2. Computational methods
Previous: 2.3 Target plane analysis
Andrea Milani
2000-06-21
![]() .
Then we need to identify a
change
.
Then we need to identify a
change ![]() in the orbital elements (with respect to Xj),
such that
in the orbital elements (with respect to Xj),
such that
![]() onto a two-dimensional subspace
onto a two-dimensional subspace
![]() ,
followed by an invertible map
,
followed by an invertible map
![]() :
:
![]() map linearly into
nonzero changes on the target plane; thus there is an inverse map
BT=AT-1. The projection
map linearly into
nonzero changes on the target plane; thus there is an inverse map
BT=AT-1. The projection
![]() is not invertible,
the preimage of each point being a 4-dimensional space. However, we
can select one change in orbital elements
is not invertible,
the preimage of each point being a 4-dimensional space. However, we
can select one change in orbital elements
![]() which
has a given displacement as image on the target plane
which
has a given displacement as image on the target plane
![]() .
The portion of the preimage contained in the confidence
ellipsoid (1) can be described by the inequality
.
The portion of the preimage contained in the confidence
ellipsoid (1) can be described by the inequality