We need now to describe the subset in the elements space containing
the orbits compatible with the observations in the sense of
(1) that lead to an impact at the same return of the VI
found in the previous step. The displacement
![]() of the last
iteration of Newton's method is negligibly small,
of the last
iteration of Newton's method is negligibly small,
![]() .
The point on the MTP of convergence of Newton's method
defines a 4-dimensional ellipsoid
.
The point on the MTP of convergence of Newton's method
defines a 4-dimensional ellipsoid
![]() of changes in orbital elements
of changes in orbital elements ![]() with respect to the VI,
such that, as long as the linear approximation applies,
with respect to the VI,
such that, as long as the linear approximation applies,
![]() implies an impact, actually one passing through the
same point on the target plane.
implies an impact, actually one passing through the
same point on the target plane.
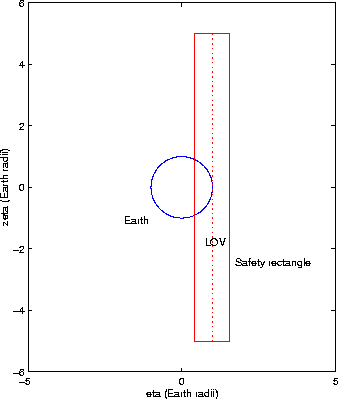
Our purpose is to define a negative observations strategy that allows
us to exclude the possibility of an impact; thus we need to select a
safety area on the MTP, such that the orbits passing outside are
certainly not dangerous. We define a rectangle
![]() ,
centered on the MTP intercept of the VI, such that in the direction of
the weak axis (eigenspace of
,
centered on the MTP intercept of the VI, such that in the direction of
the weak axis (eigenspace of ![]() ), the rectangle extends
), the rectangle extends ![]() Earth radii, and in the direction parallel to the eigenspace of
Earth radii, and in the direction parallel to the eigenspace of
![]() the rectangle spans the
the rectangle spans the
![]() region, as in
Figure 1. We are moving only 5 radii along the weak
direction, anyway much less than
region, as in
Figure 1. We are moving only 5 radii along the weak
direction, anyway much less than
![]() (which is
typically several AU); on the contrary we do not move beyond the
(which is
typically several AU); on the contrary we do not move beyond the
![]() line in the direction across the axis of the MTP confidence
boundary, because
line in the direction across the axis of the MTP confidence
boundary, because
![]() is typically less than one Earth
radius. These conditions are chosen in such a way that an orbit that
intersects the MTP outside R either fits badly the existing
observations, or cannot come too close to the Earth; however, they may
not be appropriate to a case in which
is typically less than one Earth
radius. These conditions are chosen in such a way that an orbit that
intersects the MTP outside R either fits badly the existing
observations, or cannot come too close to the Earth; however, they may
not be appropriate to a case in which ![]() is of the same order
of magnitude of
is of the same order
of magnitude of ![]() ,
as it would be the case if the impact
could take place soon after the discovery epoch.
,
as it would be the case if the impact
could take place soon after the discovery epoch.
 |
Now let ![]() be variable inside the rectangle R; for each
be variable inside the rectangle R; for each
![]() the preimage in
the preimage in ![]() is a 4-dimensional ellipsoid
is a 4-dimensional ellipsoid
![]() (at least in the linear approximation);
the preimage
(at least in the linear approximation);
the preimage
![]() of R is the union of all of the
4-dimensional ellipsoids of each point in R
of R is the union of all of the
4-dimensional ellipsoids of each point in R
This region is a generalized cylinder, topologically (but not
isometrically) equivalent to a product of a rectangle and of the
interior of an ellipsoid in 4-dimensional space. To explore it fully,
e.g. with a Monte Carlo method, is possible but computationally
expensive, being a 6-dimensional region. Thus we resort to an
approximation. The region
![]() is obtained by computing
is obtained by computing
![]() ;
the 4-dimensional ellipsoid changes with
;
the 4-dimensional ellipsoid changes with
![]() ,
thus with
,
thus with ![]() .
However,
.
However,
![]() is
very small, and so is the corresponding
is
very small, and so is the corresponding
![]() ,
at
least for impacts with low probability that occur many decades after
the initial conditions, i.e., a small change in the initial semimajor
axis moves the point on the MTP a great deal. Thus we approximate the
region XR by the Cartesian product
,
at
least for impacts with low probability that occur many decades after
the initial conditions, i.e., a small change in the initial semimajor
axis moves the point on the MTP a great deal. Thus we approximate the
region XR by the Cartesian product