2.3 Target plane analysis

Let us assume that the orbit with initial conditions X_i undergoes a close approach to the Earth at a time $t_i\gg t_0$; the Modified Target Plane (MTP) for that encounter is the plane perpendicular to the geocentric velocity at closest approach. Let this plane be ${\cal T}$ and the points on it be $T\in {\cal T}$; then there is a differentiable map

$$F_T:{\cal X} \longrightarrow {\cal T}$$

which can be explicitly computed by orbit propagation from epoch t₀to a time near t_i when the orbit crosses the MTP; the matrix DF_Tof the partial derivatives of F_T is computable by means of the state transition matrix, the solution of the variational equation. If $\Delta X= X-X_i$ is a small change in the orbital elements with respect to the reference solution X_i, then the mapping on the target plane can be approximated by its differential

$$\Delta T = DF_T \; \Delta X\ .$$

By this linear map, the ellipsoid of Eq. (1) is mapped onto the target plane as an elliptical disk with equations [Milani and Valsecchi 1999]

$$\begin{eqnarray*}\sigma^2 &\geq& \Delta T\cdot C_T \; \Delta T\\ C_T&=&\left(\G... ...ht)^{-1}\\ \Gamma_T&=&DF_T\; \Gamma_X\; \left(DF_T\right)^T\ . \end{eqnarray*}$$

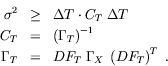
By computing the eigenvalues $\lambda_1>\lambda_2>0$ of $\Gamma_T$, we find that there is again a weak direction corresponding to the long axis of the MTP ellipse. As the time elapsed from t₀increases, the confidence region becomes longer and longer in the phase space, and simultaneously thinner and thinner (this follows from Liouville's theorem, by which the phase space 6-dimensional volume is invariant). Thus, when a close approach takes place decades after the initial epoch t₀, the two eigenvalues of $\Gamma_T$ have a very large ratio. An orbital solution that moves the MTP intersection along the weak direction results in a negligible change in the value of the target function, that is a negligible increase in the RMS of the observation residuals. On the contrary, a comparatively small change in the orthogonal direction, along the minor axis of the ellipse, would result in a significant increase of the residual RMS.

Thus the points on the MTP which can be reached with a negligible increase in the RMS are the points of the straight line which is the eigenspace of the larger eigenvalue $\lambda_1$; let T_min be the point along that line that is closest to the center of the Earth, provided it is not too far along the line (with respect to $\sqrt{\lambda_1}$). The distance d_min of T_min provides an estimate of the closest approach distance possible within the confidence ellipsoid; this estimate involves two approximations. First, the width $\sqrt{\lambda_2}$ of the ellipse is neglected; second, the nonlinear map F_T is replaced by its linearization DF_T. Both approximations can be removed, e.g., by the method of semilinear confidence boundaries described in [Milani and Valsecchi 1999]. However, for the purpose of finding VIs another approach is more efficient.