


Next: 2.3 Fourier analysis
Up: 2. Synthetic theory
Previous: 2.1 Numerical integration
The typical output of a long-term numerical integration of an orbit
consists of the time series of orbital elements (and possibly other
quantities) sampled at regular intervals, much longer than the time
step of the integration itself. This decimation of the output is
in our case combined with the digital filtering to cut off the
short-period perturbing terms. The N-body problem is strongly
degenerate, that is the spectrum of the orbital elements is divided in
two distinct regions, at high and low frequencies. This allows
filtering to be performed independently from the Fourier analysis of
the secular system, which by definition contains only the low
frequencies. This requires to design filters with performances
specifically adapted to the problem; some of the requirements are
conflicting, and in practice a suitable compromise must be reached for
an optimum performance.
The digital filtering procedure applied in the present paper is
described in detail in Carpino et al. ([1987]). Thus we only briefly
outline the algorithm and the particular choices of the main
parameters. The output of the numerical integration can be represented
as a time series of orbital elements sampled at regular intervals of
length Ts; for a generic element x
In order to produce a correct spectral representation of the time
series, it is necessary to take into account that the discrete
Fourier transform of the signal
is periodic with period equal to the sampling frequency
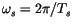
and therefore any spectral line having frequency
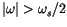 will generate a low frequency alias in the region
will generate a low frequency alias in the region
![$[-\omega_s/2,\omega_s/2]$](img11.gif) ,
more precisely at the frequency
,
more precisely at the frequency
Of course, this situation is highly undesirable, because the
interpretation of a spectrum in which real features are mixed with
aliased lines would be difficult. In order to avoid this, it is
necessary to use a sampling periodicity Ts satisfying the so-called
Nyquist criterion, according to which the sampling frequency
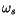 must be larger than
must be larger than
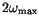 ,
where
,
where
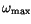 is the highest frequency present in the spectrum of the series.
In the case of the output of the numerical integration of planetary
orbits, this would mean to sample the orbital elements at least
several times per revolution of the body having the shortest orbital
period, in order to avoid aliasing from the short periodic terms
produced by its perturbation. For a long-term integration, the
adoption of such a short sampling periodicity would in turn produce a
huge amount of output: this is not only demanding from the point of
view of the computer resources, but would also make the subsequent
steps of analysis of the results very cumbersome; on the other hand,
if one is interested only in the long-periodic features of the
spectrum, the information about short periodic terms is anyway not
necessary.
A possible solution of this problem consists in the cancellation of
the high frequency components of the signal by appropriate
digital filtering techniques; after the application of a suitable
low-pass digital filter removing all short-periodic terms, the
sampling periodicity of the output can be reduced substantially
without generating aliasing. Basically the filtering procedure
consists in a linear convolution of the time series of the
orbital elements xj with a suitable finite real succession dk:
is the highest frequency present in the spectrum of the series.
In the case of the output of the numerical integration of planetary
orbits, this would mean to sample the orbital elements at least
several times per revolution of the body having the shortest orbital
period, in order to avoid aliasing from the short periodic terms
produced by its perturbation. For a long-term integration, the
adoption of such a short sampling periodicity would in turn produce a
huge amount of output: this is not only demanding from the point of
view of the computer resources, but would also make the subsequent
steps of analysis of the results very cumbersome; on the other hand,
if one is interested only in the long-periodic features of the
spectrum, the information about short periodic terms is anyway not
necessary.
A possible solution of this problem consists in the cancellation of
the high frequency components of the signal by appropriate
digital filtering techniques; after the application of a suitable
low-pass digital filter removing all short-periodic terms, the
sampling periodicity of the output can be reduced substantially
without generating aliasing. Basically the filtering procedure
consists in a linear convolution of the time series of the
orbital elements xj with a suitable finite real succession dk:
in this way the spectrum of the convolved signal
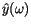 is equal to the product of the spectrum of the input signal
is equal to the product of the spectrum of the input signal
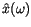 and the frequency response of the filter
and the frequency response of the filter
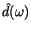 (which
is the discrete Fourier transform of the filter coefficients dk); the
filter can be designed in such a way that its frequency response is almost
zero for frequencies larger than a prescribed cutoff frequency
(which
is the discrete Fourier transform of the filter coefficients dk); the
filter can be designed in such a way that its frequency response is almost
zero for frequencies larger than a prescribed cutoff frequency
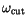
For the filtered signal yj the Nyquist criterion becomes
of course, in the actual design of the filter,
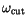 must be
selected in such way as to preserve the spectral features of interest
(in our case, the region of the spectrum corresponding to secular terms).
must be
selected in such way as to preserve the spectral features of interest
(in our case, the region of the spectrum corresponding to secular terms).
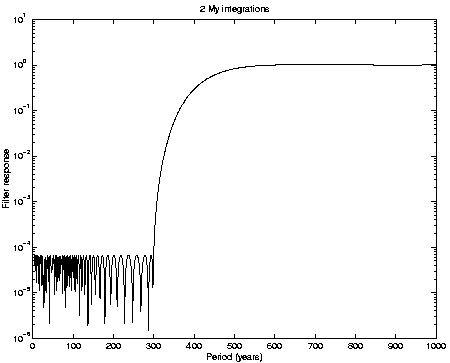
Figure:
Frequency response of the digital filter, as used in the 2
Myr integrations.
 |
For the computation of synthetic proper elements, we have used a
filter with decimation 100; e.g., in our 2 Myr integrations, we have
used an input sampling frequency of one data point every 2 yr, and the
output contains one data point every 200 yr. Long frequency aliases
can be produced, as a result of a beat with the input frequency, only
if they have periods less than the input Nyquist period of 4 yr; thus,
in the outer asteroid belt, the perturbations with a frequency close
to the mean motion cannot be responsible for spurious long periodic
terms.
The frequency response of this filter is shown in
Figure 1, in particular the dark band is for periods
up to
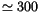 yr with response
yr with response
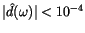 ,
and
the pass band is for periods above
,
and
the pass band is for periods above
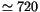 yr with response
yr with response
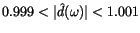 .
In this way the short periodic
perturbations are removed from the filtered output, while the secular
perturbations are not significantly distorted. Note that the response
at zero frequency is
.
In this way the short periodic
perturbations are removed from the filtered output, while the secular
perturbations are not significantly distorted. Note that the response
at zero frequency is
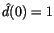 ;
this implies that the long term
average is preserved. Moreover, the coefficients of the filter we are
using are symmetric, that is
dm=d-m. In case the filter is
applied to an angle variable, provided the angle time series is
transformed into a continuous real function by adding
;
this implies that the long term
average is preserved. Moreover, the coefficients of the filter we are
using are symmetric, that is
dm=d-m. In case the filter is
applied to an angle variable, provided the angle time series is
transformed into a continuous real function by adding 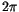 times the
number of revolutions, the filter output has the same long term slope
and phase as the original data. This is essential to be able to use
the filter output to fit frequencies and phases. For the 10 Myr
integrations, to avoid excessive output, we have used the same filter
with one input data point every 5 yr.
times the
number of revolutions, the filter output has the same long term slope
and phase as the original data. This is essential to be able to use
the filter output to fit frequencies and phases. For the 10 Myr
integrations, to avoid excessive output, we have used the same filter
with one input data point every 5 yr.



Next: 2.3 Fourier analysis
Up: 2. Synthetic theory
Previous: 2.1 Numerical integration
Andrea Milani
2000-10-03