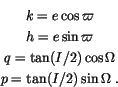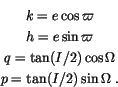Next: 2.4 Semimajor axis and
Up: 2. Synthetic theory
Previous: 2.2 Digital filtering
2.3 Fourier analysis
The procedure to extract proper eccentricity and inclination, and the
corresponding proper frequencies, is a modified form of Fourier
analysis, which is adapted from the synthetic theory method introduced
in Carpino et al. ([1987]), and further improved by Milani
([1993,1994]).
The procedure includes three steps. First, the forced secular
perturbations, which have known frequencies, are removed from the
filtered time series for the equinoctal elements
Given the fundamental frequencies
g5,g6,g7 of the precession of
perihelia of Jupiter, Saturn and Uranus respectively, we remove the
Fourier components with these frequencies from (k,h). Given the
fundamental frequencies
s6,s7,s8 of the precession of the nodes
of Saturn, Uranus and Neptune respectively, we remove the Fourier
components with these frequencies from (q,p).
Second, we compute the time series of the free arguments
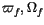 of the oscillation in the planes (k,h) and
(q,p) respectively. This is done by computing the polar angles in
these two planes, by adding multiples of
of the oscillation in the planes (k,h) and
(q,p) respectively. This is done by computing the polar angles in
these two planes, by adding multiples of 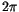 to obtain a continous
function. Finally by a linear least squares fit we obtain an estimate
of the proper frequencies g, the slope of
to obtain a continous
function. Finally by a linear least squares fit we obtain an estimate
of the proper frequencies g, the slope of 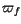 ,
and s, the
slope of
,
and s, the
slope of 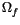 .
Third, we perform Fourier extraction of the proper mode. This can be
done in two ways, as discussed in Milani ([1994]). Either the
Fourier component with period
.
Third, we perform Fourier extraction of the proper mode. This can be
done in two ways, as discussed in Milani ([1994]). Either the
Fourier component with period 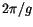 is extracted from the time
series
(k(t),h(t)); or the component with period
is extracted from the time
series
(k(t),h(t)); or the component with period 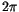 is extracted
from the data expressed as functions of
is extracted
from the data expressed as functions of 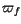 ,
that is
,
that is
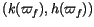 .
The results would be identical if the
proper oscillation was a linear one, but for non negligible
eccentricity the higher order terms are important (Milani and Knezevic [1990]) and the latter algorithm leads to more stable
proper elements; thus we have used it. The same applies to the
inclination related plane, and we have used the extraction of the
component with period
.
The results would be identical if the
proper oscillation was a linear one, but for non negligible
eccentricity the higher order terms are important (Milani and Knezevic [1990]) and the latter algorithm leads to more stable
proper elements; thus we have used it. The same applies to the
inclination related plane, and we have used the extraction of the
component with period 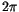 from
from
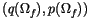 .
The
amplitudes of these proper modes are the proper elements ep and
.
The
amplitudes of these proper modes are the proper elements ep and
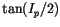 ;
the latter is then converted to the more usual
;
the latter is then converted to the more usual 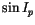 .
One of the main advantages of the synthetic method is the availability
of a stability test for each single set of proper elements computed in
this way. In our previous work, with analytical proper elements, we
needed specific numerical tests to check the stability of the results
in a few supposedly representative examples; e.g., in the paper
Milani and Knezevic ([1994]) we tested only 35 asteroids.
In the computation of synthetic proper elements, a numerical
integration over a long enough time interval [0,T] has to be
performed. Given the output of the same integration, the same
algorithm described in this Section can be applied to shorter time
intervals
.
One of the main advantages of the synthetic method is the availability
of a stability test for each single set of proper elements computed in
this way. In our previous work, with analytical proper elements, we
needed specific numerical tests to check the stability of the results
in a few supposedly representative examples; e.g., in the paper
Milani and Knezevic ([1994]) we tested only 35 asteroids.
In the computation of synthetic proper elements, a numerical
integration over a long enough time interval [0,T] has to be
performed. Given the output of the same integration, the same
algorithm described in this Section can be applied to shorter time
intervals
![$[t_j,t_j+\Delta T]$](img39.gif) ,
beginning at initial times
tj,
j=1,..,N, in such a way that t1=0,
,
beginning at initial times
tj,
j=1,..,N, in such a way that t1=0,
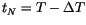 .
For each of
these ``running boxes'' a value of the proper elements
.
For each of
these ``running boxes'' a value of the proper elements
 and of the proper frequencies is obtained, and the dispersion of these
N values can be used to estimate the stability in time of the
results. As an example, for the 2 Myr integrations we have used N=11
running boxes of length
and of the proper frequencies is obtained, and the dispersion of these
N values can be used to estimate the stability in time of the
results. As an example, for the 2 Myr integrations we have used N=11
running boxes of length
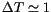 Myr; for the 10 Myr
integrations, N=9 and
Myr; for the 10 Myr
integrations, N=9 and
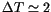 Myr. The dispersion of the
values of some proper element E in the different boxes can be
measured by the root mean square
Myr. The dispersion of the
values of some proper element E in the different boxes can be
measured by the root mean square 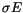 (of the differences of the
values computed in each box with respect to the value computed over
the entire time span) and by the maximum difference
(of the differences of the
values computed in each box with respect to the value computed over
the entire time span) and by the maximum difference 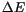 among
the values computed in all the boxes.
among
the values computed in all the boxes.



Next: 2.4 Semimajor axis and
Up: 2. Synthetic theory
Previous: 2.2 Digital filtering
Andrea Milani
2000-10-03