The other case of ostensibly protected behavior occurs for the near-Earth orbits of the Kozai class, according to the classification of [Milani et al. 1989]. The name comes from a namesake asteroid, (3040) Kozai, but also from the author of the seminal work on this subject [Kozai 1962].
The evidence from numerical integrations is that of a dynamical
behavior as in the example of
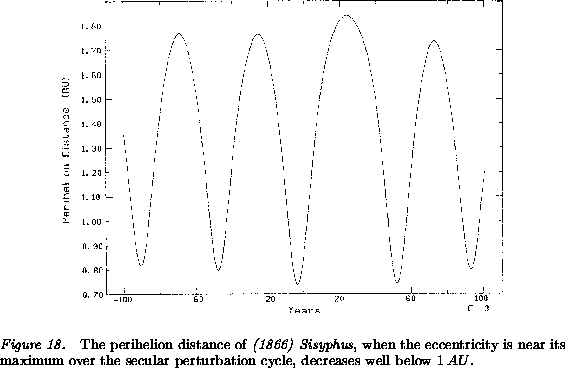
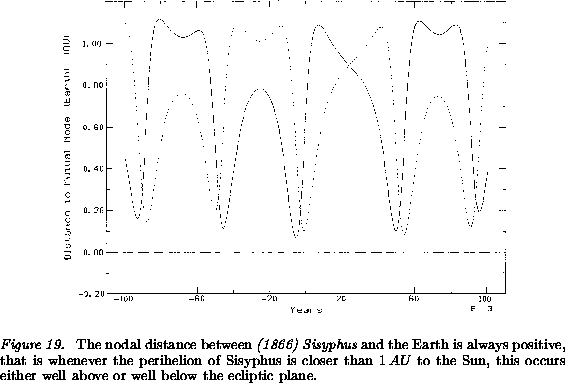
Figures 18-19. There are many asteroids
with perihelion distance q which can, as a result of the secular
perturbations to the eccentricity, decrease below ![]() , and
nevertheless there are no node crossings, that is, the nodal distance
is always positive. This happens only for orbits with significant
inclination, because in this case the evolution of e and
, and
nevertheless there are no node crossings, that is, the nodal distance
is always positive. This happens only for orbits with significant
inclination, because in this case the evolution of e and ![]() are strongly coupled. In the example of the
Figures 18-19, that is the Mars-crossing
asteroid (1866) Sisyphus, q can be as low as
are strongly coupled. In the example of the
Figures 18-19, that is the Mars-crossing
asteroid (1866) Sisyphus, q can be as low as ![]() , and
at the same time the nodes are above
, and
at the same time the nodes are above ![]() , because the argument
of perihelion has a value either around
, because the argument
of perihelion has a value either around ![]() or around
or around ![]() when the eccentricity is at a maximum.
when the eccentricity is at a maximum.
To understand this mechanism of avoidance of node crossings we need to
model the secular perturbations on ![]() ; for this
we resort again to the averaging principle, but in this case the
average is performed on both the fast angles
; for this
we resort again to the averaging principle, but in this case the
average is performed on both the fast angles ![]() , assuming
that there is no mean motion resonance, that is the torus of the mean
anomalies is in this case covered uniformly (more exactly, in an
ergodic way, see [Arnold 1976]). The averaged Hamiltonian is
, assuming
that there is no mean motion resonance, that is the torus of the mean
anomalies is in this case covered uniformly (more exactly, in an
ergodic way, see [Arnold 1976]). The averaged Hamiltonian is
![]()
where ![]() is the unperturbed 2-body Hamiltonian,
is the unperturbed 2-body Hamiltonian, ![]() is the direct perturbing function (with D the distance between the
asteroid and the planet, m the mass of the perturbing planet) and
is the direct perturbing function (with D the distance between the
asteroid and the planet, m the mass of the perturbing planet) and
![]() is the indirect part of the perturbing function. By a
classical result, the average over the anomalies of the indirect
perturbing function is zero, thus
is the indirect part of the perturbing function. By a
classical result, the average over the anomalies of the indirect
perturbing function is zero, thus
![]()
There are two main methods to compute the averaged perturbing function
![]() . It is possible to expand the perturbing potential in series,
with the eccentricities and inclinations as small parameters. That
is, R is expanded as a Taylor series in e,I,e', I', and for each
order as a Fourier series in the angles
. It is possible to expand the perturbing potential in series,
with the eccentricities and inclinations as small parameters. That
is, R is expanded as a Taylor series in e,I,e', I', and for each
order as a Fourier series in the angles ![]() . The
classical D'Alembert rules, which result from the invariance of the
problem with respect to orthogonal transformations, strongly constrain
the terms which can appear with non zero coefficient in such a series,
and it turns out that only the even order terms are allowed; see
e.g. [Milani 1994]. Thus the lowest order terms containing the
eccentricities and the inclinations are quadratic, and if the theory
is truncated to degree two the secular perturbations can be described,
in suitable variables, as the solutions of a system of linear
differential equations.
. The
classical D'Alembert rules, which result from the invariance of the
problem with respect to orthogonal transformations, strongly constrain
the terms which can appear with non zero coefficient in such a series,
and it turns out that only the even order terms are allowed; see
e.g. [Milani 1994]. Thus the lowest order terms containing the
eccentricities and the inclinations are quadratic, and if the theory
is truncated to degree two the secular perturbations can be described,
in suitable variables, as the solutions of a system of linear
differential equations.
The method outlined above is the classical one, introduced by Laplace
and others more than 200 years ago, and it gives a reasonable first
approximation of the secular perturbations of the orbits of moderately
perturbed planets with low eccentricities and inclinations, such as the
major planets Venus to Neptune. This approximation fails when
eccentricity and inclination are large; in this case the largest term
in the perturbing function neglected by the Laplace linear theory is
the one with ![]() .
.
An integrable first approximation, different from a linear system, was
introduced by [Kozai 1962]. Let us assume that the perturbing planet
is on a circular orbit, and on the reference plane: e'=I'=0. The
argument applies also to the case of many perturbing planets, provided
the orbits are all circular and all on the same plane. Then the
problem averaged over ![]() can be described in the way already
introduced by Gauss, as the gravitational problem defined by a mass
distributed in rings along the planetary orbits; the perturbing
potential is axisymmetric with respect to the axis through the Sun and
orthogonal to the plane of the planets, and the component of the
angular momentum of the asteroid orbit along the same axis is
preserved.
can be described in the way already
introduced by Gauss, as the gravitational problem defined by a mass
distributed in rings along the planetary orbits; the perturbing
potential is axisymmetric with respect to the axis through the Sun and
orthogonal to the plane of the planets, and the component of the
angular momentum of the asteroid orbit along the same axis is
preserved.
In terms of ![]() and of the keplerian orbital elements
and of the keplerian orbital elements
![]() , the averaged Hamiltonian is
independent of
, the averaged Hamiltonian is
independent of ![]() and of
and of ![]() , and the two conjugate
variables are integrals: they are proportional to
, and the two conjugate
variables are integrals: they are proportional to ![]() and to
and to
![]()
respectively. In conclusion
![]()
is a one degree of freedom Hamiltonian, with two parameters L and
Z. This averaged problem is integrable; once a and
![]() are fixed, the secular evolution can be
described as a curve in the
are fixed, the secular evolution can be
described as a curve in the ![]() plane; I is a function of
e, which can be deduced from Z=const, and
plane; I is a function of
e, which can be deduced from Z=const, and ![]() does not
matter. This curve can be drawn as level curve of the function
does not
matter. This curve can be drawn as level curve of the function ![]() .
.
For low inclination the ![]() curves in the
curves in the ![]() plane
are not very different from e=const lines; but for large I, the
coupling terms such as the one with
plane
are not very different from e=const lines; but for large I, the
coupling terms such as the one with ![]() become dominant, and the eccentricity undergoes large relative changes
as
become dominant, and the eccentricity undergoes large relative changes
as ![]() circulates. Below a critical value of Z/L, the topology
of the level curves of
circulates. Below a critical value of Z/L, the topology
of the level curves of ![]() changes and a separatrix appears,
bounding a region where
changes and a separatrix appears,
bounding a region where ![]() librates, typically around either
librates, typically around either
![]() or
or ![]() . This Kozai resonance is especially
effective in keeping the perihelion of the asteroid out of the plane
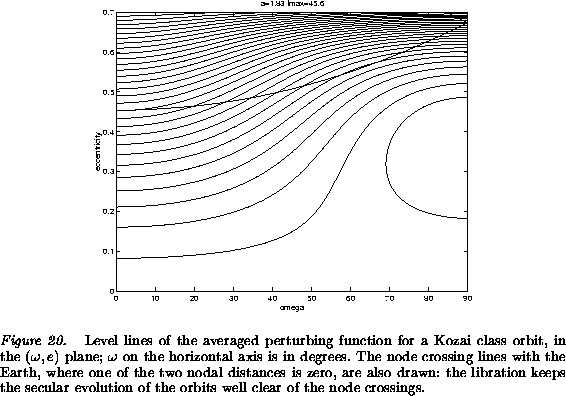
of the perturbing planets. Figure 20 shows the phase
space of the averaged problem, for values of the initial conditions
consistent with those of the asteroid (3040) Kozai. A large
libration region is ``safe'' from node crossings; there are also many
solution curves where a strong
. This Kozai resonance is especially
effective in keeping the perihelion of the asteroid out of the plane
of the perturbing planets. Figure 20 shows the phase
space of the averaged problem, for values of the initial conditions
consistent with those of the asteroid (3040) Kozai. A large
libration region is ``safe'' from node crossings; there are also many
solution curves where a strong ![]() coupling achieves the same
result, because
coupling achieves the same
result, because ![]() can be near 0, but only for e near its
minimum value.
can be near 0, but only for e near its
minimum value.
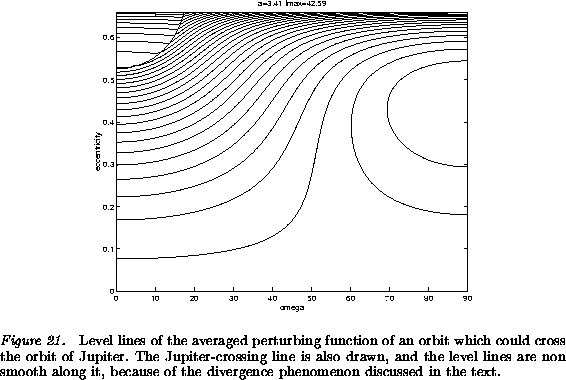
The same mechanism protects the high inclination asteroids at the
outer edge of the main belt from close approaches to Jupiter, as in
Figure 21, because ![]() implies that not only
the perihelion, but also the aphelion is out of the plane of the
planetary orbits. When on the contrary the planet with which collision
could occur has a semimajor axis a' very close to a, then the node
crossings are avoided when the nodal points are at perihelion and at
aphelion, that is for
implies that not only
the perihelion, but also the aphelion is out of the plane of the
planetary orbits. When on the contrary the planet with which collision
could occur has a semimajor axis a' very close to a, then the node
crossings are avoided when the nodal points are at perihelion and at
aphelion, that is for ![]() and
and ![]() , as in
Figure 22 and in [Michel and Thomas 1996]. For very high
inclination the same averaged dynamics can result in increases of the
eccentricity up to values very close to 1, and then the fate of the
orbit can be to encounter the surface of the Sun; however this
requires a very high initial inclination, and occurs almost only to
comets [Bailey et al. 1992].
, as in
Figure 22 and in [Michel and Thomas 1996]. For very high
inclination the same averaged dynamics can result in increases of the
eccentricity up to values very close to 1, and then the fate of the
orbit can be to encounter the surface of the Sun; however this
requires a very high initial inclination, and occurs almost only to
comets [Bailey et al. 1992].
The behavior of the Kozai class asteroids implies that the Öpik-Kessler methods to compute probability of collision might fail, in that they give a finite probability to collisions which can not occur at all. A more flexible method to compute frequency of close approaches and probability of collision, which could take into account the actual occurrence of node crossings, was developed over many years, beginning with the basic formulas devised by [Öpik 1951], later extended and developed by [Wetherill 1967], [Greenberg 1982], and many others. The basic geometric idea is as follows. When two osculating orbits have a small nodal distance, it is possible to approximate a short span of both ellipses with their tangent lines at the respective nodal points, parametrized in such a way that the velocity at the nodal point is the same on the ellipses and on the straight lines. Then the distance, as a function of the parameters on these straight lines, is an easily computed quadratic form. From this approximate distance function it is possible to compute analytically the time span spent by the two orbits in the region where the distance is less than a given impact parameter.
The large scale tests performed in [Milani et al. 1990] show that the
Öpik-Wetherill method is very effective in predicting the number of
close approaches which is possible at each actual node crossing, thus
it solves the problem of computing the probability of collision for
the Kozai class, provided the secular evolution of the orbital
elements ![]() is available, e.g. from numerical
integrations. It is also a very effective method to detect Toro class
orbits, which by definition violate the formula, by avoiding close
approaches at actual node crossings. This method can not be used for
low inclination and almost tangent encounters, the same difficulties
found with the Kessler method.
is available, e.g. from numerical
integrations. It is also a very effective method to detect Toro class
orbits, which by definition violate the formula, by avoiding close
approaches at actual node crossings. This method can not be used for
low inclination and almost tangent encounters, the same difficulties
found with the Kessler method.
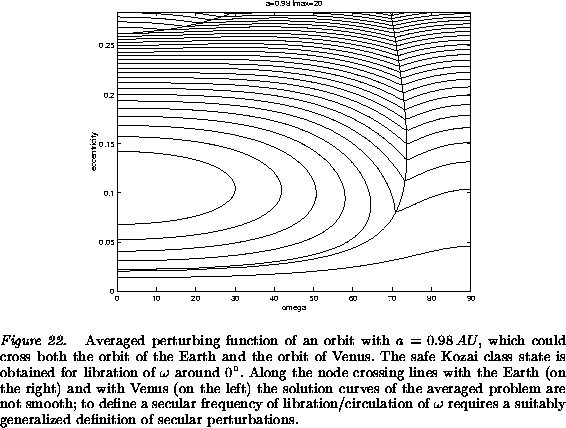
The Figures 20, 21 and especially
22 show that the level curves of the averaged
Hamiltonian ![]() are not smooth on the node crossing lines. Indeed
the integral over the torus of the variables
are not smooth on the node crossing lines. Indeed
the integral over the torus of the variables ![]() is an
improper one, and it is convergent because the singularity of
collision is a pole of order one. On the contrary, if the averaging is
applied to the right hand side of the equation of motion, the
singularity of collision is a pole of order two, and the improper
integral over the torus is not convergent. Thus the very meaning of
the secular perturbation equations is uncertain.
is an
improper one, and it is convergent because the singularity of
collision is a pole of order one. On the contrary, if the averaging is
applied to the right hand side of the equation of motion, the
singularity of collision is a pole of order two, and the improper
integral over the torus is not convergent. Thus the very meaning of
the secular perturbation equations is uncertain.
Recently it has been shown [Gronchi and Milani 1998] that the averaged
Hamiltonian ![]() , although not smooth, has enough regularity -in a
neighbourhood of the node crossing line- to allow a generalized
definition of secular perturbation equations. This has been obtained
by using the Öpik-Wetherill approximation of a short stretch of the
orbits near the mutual node with straight lines. The approximate
distance function d between the points on the straight lines is a
quadratic form, and then the integral of 1/d over the torus can be
computed either analytically or semi-analytically; the singularity of
1/d at exact node crossing is used to remove the singularity from
the improper integral (Kantorovic method to compute improper
integrals).
, although not smooth, has enough regularity -in a
neighbourhood of the node crossing line- to allow a generalized
definition of secular perturbation equations. This has been obtained
by using the Öpik-Wetherill approximation of a short stretch of the
orbits near the mutual node with straight lines. The approximate
distance function d between the points on the straight lines is a
quadratic form, and then the integral of 1/d over the torus can be
computed either analytically or semi-analytically; the singularity of
1/d at exact node crossing is used to remove the singularity from
the improper integral (Kantorovic method to compute improper
integrals).
In this way it is possible to compute secular orbits even in the
presence of node crossings, and thus to compute the secular frequency
of circulation/libration of ![]() and of circulation of
and of circulation of
![]() . As a matter of principle, this allows one to use the Kozai
theory as a first integrable step in a perturbation theory, to study
secular resonances, and to compute proper elements even for
planet-crossing orbits; the theory developed in [Gronchi and Milani 1998]
contains explicit algorithms for this, but most of the work remains to
be done.
. As a matter of principle, this allows one to use the Kozai
theory as a first integrable step in a perturbation theory, to study
secular resonances, and to compute proper elements even for
planet-crossing orbits; the theory developed in [Gronchi and Milani 1998]
contains explicit algorithms for this, but most of the work remains to
be done.