
An Earth-crossing orbit of the ``normal'' type, that is of the
Geographos class, undergoes close approaches at random, during
comparatively short time spans around the epochs of the node
crossings. However, there are orbits which are Near Earth in that
they satisfy ![]() , and nevertheless close approaches either
do not take place at all, or take place more seldom and with larger
distances from the Earth than the statistical theories would predict.
, and nevertheless close approaches either
do not take place at all, or take place more seldom and with larger
distances from the Earth than the statistical theories would predict.
The protection mechanisms which can be responsible for this ``Earth-avoidance'' behavior are essentially two: either node crossings occur, but close approaches do not take place even when the distances between the two orbits would allow, or node crossings do not occur. In this Section we discuss the first case, that is the Toro class, according to the classification of [Milani et al. 1989].
The empirical evidence for the existence of a Toro class of dynamical
behavior is in a number of examples found by several authors,
starting from [Janiczek et al. 1972], and in a systematic way in the large
database of planet-crossing orbits generated by the PROJECT
SPACEGUARD, which contain thousands of figures like
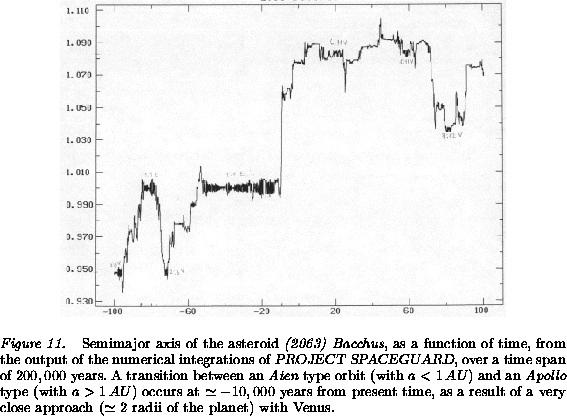
Figures 11-13. The Figures we have
selected refer to the asteroid (2063) Bacchus, and show the
`normal' Geographos class behavior, with semimajor axis jumping at
random as a result of close approaches to both the Earth and Venus
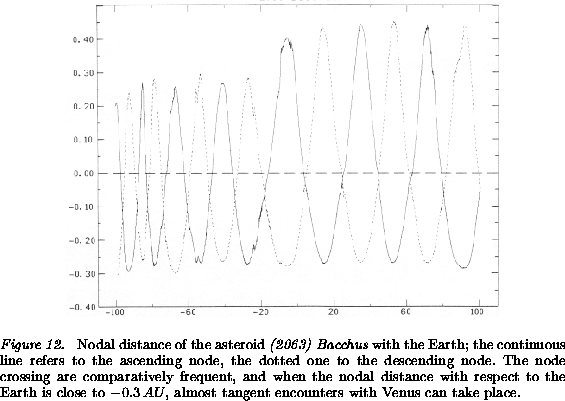
(Figure 11) around the node crossing epochs
(e.g. Figure 12 shows the node crossings with the
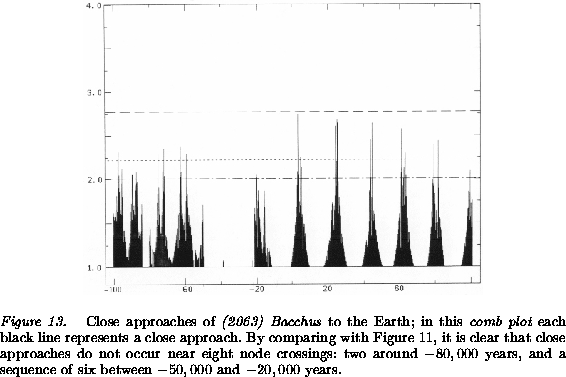
Earth). However, there are some node crossings with the Earth which do
not correspond to close approaches: in the Figure 13
these ``safe intervals'' are apparent as gaps in the comb. In this
example the protection mechanism is active when the semimajor axis of
(2063) Bacchus is close to ![]() , and therefore must be
related to the 1:1 resonance, that is to a state of ``Earth's
Trojan''.
, and therefore must be
related to the 1:1 resonance, that is to a state of ``Earth's
Trojan''.
To model in the simplest way this behavior, let us assume the planet
-e.g. the Earth- is in a circular orbit with radius a', and the
asteroid has orbital elements ![]() such that -for some
time around the node crossing epoch- the distance from the Sun at one
node is close to a': let us say
such that -for some
time around the node crossing epoch- the distance from the Sun at one
node is close to a': let us say
![]()
note that the value of the longitude of the node ![]() does not
matter. For a time span short with respect to the frequencies of the
secular perturbations, but longer than the orbital period, the only
elements which change in a significant way are the anomalies
does not
matter. For a time span short with respect to the frequencies of the
secular perturbations, but longer than the orbital period, the only
elements which change in a significant way are the anomalies
![]() of both the asteroid and the planet. Since these are
angle variables, the short term dynamics can be described on a phase
space which is a torus, the Cartesian product of two circles; a
torus can be represented, as in Figure 14, as a square
with the opposite sides identified.
of both the asteroid and the planet. Since these are
angle variables, the short term dynamics can be described on a phase
space which is a torus, the Cartesian product of two circles; a
torus can be represented, as in Figure 14, as a square
with the opposite sides identified.
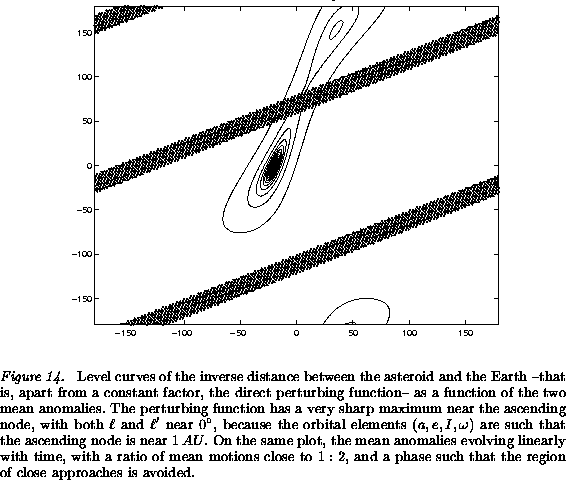
Figure 14 shows the level lines of the gravitational
potential of the Earth, as felt by an asteroid in an Earth-crossing
orbit very close to a node crossing (the distance at the ascending
node is less than ![]() ). The gravitational potential has a very
sharp maximum near the node, while the perturbation due to the Earth
is very small elsewhere. As time goes by, the changes in the anomalies
). The gravitational potential has a very
sharp maximum near the node, while the perturbation due to the Earth
is very small elsewhere. As time goes by, the changes in the anomalies
![]() of both orbits can be described approximately by the
linear functions of time
of both orbits can be described approximately by the
linear functions of time ![]() ,
with n,n' the mean motions. For values of a such that the ratio
n/n' is close to a fraction q/p with q,p small integers, that is
near a mean motion resonance, the orbit does not spread
uniformly on the torus, but can avoid significant portions of it,
possibly including the region around the maximum, that is avoiding
close approaches.
,
with n,n' the mean motions. For values of a such that the ratio
n/n' is close to a fraction q/p with q,p small integers, that is
near a mean motion resonance, the orbit does not spread
uniformly on the torus, but can avoid significant portions of it,
possibly including the region around the maximum, that is avoiding
close approaches.
That such a temporary protection mechanism can occur at some node
crossings is clear, but the question is: does this happen by chance?
By means of a purely cinematical description, as given above, we would
expect that if a is close enough to a resonant value, the orbit
will have the right phase ![]() for protection at some node
crossing, and then have a wrong phase in some later node crossing,
essentially at random. This is not the case because the mean anomaly
of the asteroid, and therefore the phase of the resonance (some
critical argument of the form
for protection at some node
crossing, and then have a wrong phase in some later node crossing,
essentially at random. This is not the case because the mean anomaly
of the asteroid, and therefore the phase of the resonance (some
critical argument of the form ![]() some combination of
some combination of
![]() ), does not change linearly but is
subject to a kind of restoring force. The restoring force is of
course stronger the closer are the two orbits, and has very high
values near the node crossings, and near the maximum point on the
torus.
), does not change linearly but is
subject to a kind of restoring force. The restoring force is of
course stronger the closer are the two orbits, and has very high
values near the node crossings, and near the maximum point on the
torus.
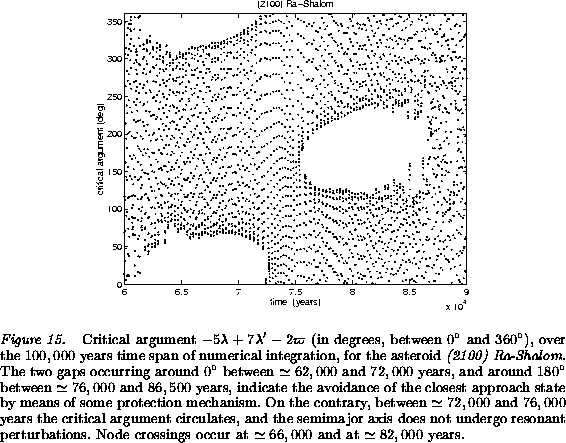
The behavior of the critical argument of a Toro class orbit is shown
as a function of time in Figure 15, from
[Milani and Baccili 1998]. The plot shows ``avoidance'', in the sense that the
dangerous position with both the Earth and the asteroid near the
ascending node is avoided, but only when the nodal distance is small
(less than ![]() in this example). This Figure is typical of
the Toro class orbits, including the case of the namesake asteroid
(1685) Toro, Figure 6 in [Milani et al. 1989].
in this example). This Figure is typical of
the Toro class orbits, including the case of the namesake asteroid
(1685) Toro, Figure 6 in [Milani et al. 1989].
Thus the protective effect of mean motion resonance occurs much more
often than it would take place if it was controlled only by chance.
Figure 15 is enough to understand that the restoring
force due to the perturbations from the Earth acting on the asteroid
mean anomaly ![]() is pushing the orbit away from the collision.
is pushing the orbit away from the collision.
This ``negative attraction'' effect is somewhat counter our earth-bound
intuition, but in fact is another form of the first paradox of
astrodynamics, well known to astronauts. If an asteroid (or
spacecraft) is pushed forward along its orbit by some perturbing
acceleration acting along track (it does not matter if this
acceleration is due either to the attraction of a third body, or to
the action of rocket engines), the orbital energy increases, the
semimajor axis increases, and the mean motion decreases, thus the
asteroid (spacecraft) is pushed backward; the displacement produced by
an along track acceleration ![]() is
is ![]() .
.
To transform this intuitive explanation in a rigorous mathematical
argument we need to resort to a semianalytical theory, obtained by
averaging [Milani and Baccili 1998]. If ![]() is a slow
variable, because of
is a slow
variable, because of ![]() , then there is another variable
, then there is another variable
![]() obtained together with
obtained together with ![]() by a unimodular
transformation, that is c,d are integers and pd-qc=1. Such
by a unimodular
transformation, that is c,d are integers and pd-qc=1. Such ![]() is a fast angle, and averaging with respect to
is a fast angle, and averaging with respect to ![]() is a good
approximation by the averaging principle [Arnold 1976]; if the
averaging is performed over a single angle variable, the averaging
principle is a rigorous theorem, with estimate of the error done in
neglecting the short periodic terms. Then we are left with the
semi-averaged Hamiltonian, still depending upon one angle variable:
is a good
approximation by the averaging principle [Arnold 1976]; if the
averaging is performed over a single angle variable, the averaging
principle is a rigorous theorem, with estimate of the error done in
neglecting the short periodic terms. Then we are left with the
semi-averaged Hamiltonian, still depending upon one angle variable:
![]()
where ![]() are the action variables conjugate to the angle
variables
are the action variables conjugate to the angle
variables ![]() ,
, ![]() is the Hamiltonian of the 2-body
unperturbed problem transformed to the new variables, and R is the
usual perturbing function of the 3-body problem, also depending upon
the other orbital elements, especially
is the Hamiltonian of the 2-body
unperturbed problem transformed to the new variables, and R is the
usual perturbing function of the 3-body problem, also depending upon
the other orbital elements, especially ![]() which controls the
nodal distance.
which controls the
nodal distance.
For the semi-averaged Hamiltonian ![]() , the fast angle
, the fast angle ![]() is a cyclic variable, hence T is an integral of motion; once the
value of T is fixed by the initial conditions,
is a cyclic variable, hence T is an integral of motion; once the
value of T is fixed by the initial conditions, ![]() is a function
of
is a function
of ![]() only. If we avoid being confused by too many changes of
variables, and write the result as a function of some more usual
variable, such as the Delaunay
only. If we avoid being confused by too many changes of
variables, and write the result as a function of some more usual
variable, such as the Delaunay ![]() , with
, with ![]() the gravitational constant in Gauss' form,
the gravitational constant in Gauss' form,
![]()
with ![]() the averaged perturbing function. We can now
understand the ``repulsive'' restoring force: the first derivative of
the averaged perturbing function. We can now
understand the ``repulsive'' restoring force: the first derivative of
![]() with respect to L is n-(q/p)n', zero at the exact resonance;
the second derivative is always negative.
with respect to L is n-(q/p)n', zero at the exact resonance;
the second derivative is always negative.
Thus the qualitative behavior of the semi-averaged Hamiltonian system can be understood by comparing with the simple Hamiltonian
![]()
when the nodal distance is small, V(x) has a sharp minimum near the
node. But the Hamiltonian is concave with respect to y, and
therefore the minima of the potential energy are avoided, exactly as the
maxima in the more familiar case with convexity with respect to y.
When the nodal distance ![]() , the value of the minimum
, the value of the minimum ![]() , and whatever the initial value of K there is an avoidance
region near the singularity.
, and whatever the initial value of K there is an avoidance
region near the singularity.
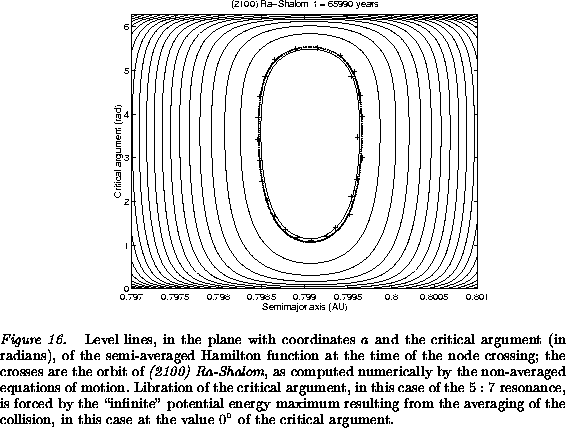
This behavior is shown in Figure 16, based on an
explicit computation of ![]() by numerical quadrature, for
values of the other elements
by numerical quadrature, for
values of the other elements ![]() such that the nodal
distance is very small. The changes in the elements different from
such that the nodal
distance is very small. The changes in the elements different from ![]() are driven by the secular perturbations, rather than by the
resonant interaction with the Earth. Thus we can consider the problem
to be defined by the semi-averaged Hamiltonian
are driven by the secular perturbations, rather than by the
resonant interaction with the Earth. Thus we can consider the problem
to be defined by the semi-averaged Hamiltonian ![]() , depending
upon time through the slow variables
, depending
upon time through the slow variables ![]() . This is
the nominal situation to apply the adiabatic invariant theory
[Henrard 1993], by which the solutions follow closely the guiding
trajectories provided by the solution of the system
. This is
the nominal situation to apply the adiabatic invariant theory
[Henrard 1993], by which the solutions follow closely the guiding
trajectories provided by the solution of the system ![]() in
the
in
the ![]() plane for fixed values of the other
elements. That is, there is an ``almost integral'', the adiabatic
invariant, which can be computed by means of the area enclosed by the
level lines of
plane for fixed values of the other
elements. That is, there is an ``almost integral'', the adiabatic
invariant, which can be computed by means of the area enclosed by the
level lines of ![]() in the
in the ![]() plane.
plane.
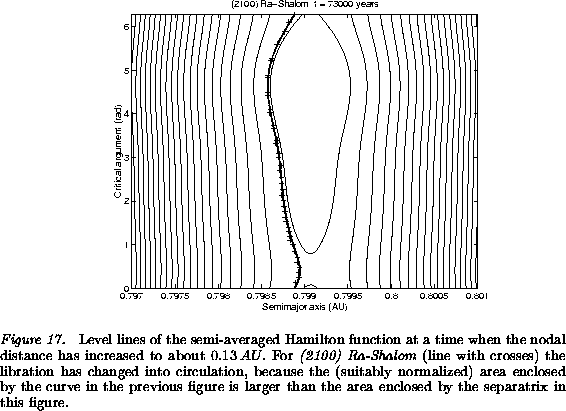
When the area enclosed by the separatrix curve (which is the curve through the saddle point, corresponding to the minimum distance) becomes smaller than the area required by the adiabatic invariant, then the guiding trajectory changes topology, and the solution switches from libration to circulation, as shown in Figure 17. This explains the apparently ``astute'' behavior of the Toro class asteroids: whenever the perturbation due to close approaches is strong, the orbit switches to a libration state, avoiding encounters at the node; when the nodal distance increases again, the potential well is not deep enough and confinement in the libration region does not occur.
The Toro state in most cases does not last for a very long time,
because resonances can protect from close approaches to one planet but
can not protect for a significant span of time from close approaches
to two planets, for the simple reason that the planets are not
resonant among them. Thus all the Toro class asteroids change their
dynamical state as a result of a close approach to a planet different
from the one they are protected from, typically after a time span of a
few 10,000 years. The only known exceptions are orbits which cross
only the orbit of Mars, such as the Eros clones studied by
[Michel et al. 1998]; if the perihelion is well above ![]() , a Toro-like
state with Mars can protect from close approaches, even for millions of
years.
, a Toro-like
state with Mars can protect from close approaches, even for millions of
years.
It is important to remember again that all the planet-crossing orbits are strongly chaotic, thus the long term behavior of all the orbits can not be predicted; in particular, the time span of residence of a specific orbit in a Toro state with a specific resonance is unpredictable. As an example, the time in which (2063) Bacchus either has been, or will be, an Earth Trojan can not be predicted, although it has to be expected that it will get there eventually.