The attempts to model the occurrence of both close approaches and collisions for planet-crossing orbits have been based upon a statistical approach, starting from the pioneering effort by Öpik, see [Öpik 1951]. A statistical theory can be constructed by adopting three simplifying assumptions:
[1] The orbits between two consecutive close approaches are assumed to be regular and modeled in some simplified way, such that an explicit computation is possible. In the simplest possible approach, the orbits are modeled as keplerian ellipses with constant semimajor axis a, eccentricity e and inclination I, uniformly precessing with time; more elaborate models exploit secular perturbation theories, obtained by either analytical or semianalytical methods, in which the constants of the motion are ``proper'' a, e and I as opposed to the corresponding instantaneous, or ``osculating'', elements.
[2] Close approaches and collisions are modeled as purely random events. More specifically, whenever the keplerian ellipses representing the osculating orbits of one asteroid and one planet are close enough to allow for a close approach, the position of the planet and of the asteroid on the orbit (i.e. the anomalies) are assumed to be randomly distributed and uncorrelated; mean motion resonances, which constrain the two anomalies, are not allowed in the model. Each close approach is seen as a random event uncorrelated with any previous one.
[3] The orbital elements 
of the asteroid are
assumed to change only as a result of close approaches; in the more
refined theories, this applies to the proper elements. Since at deep
close approaches these changes can be computed e.g. by a hyperbolic
two-body encounter approximation, the orbital evolution can be
described as a random walk. For each present state, the probability
(hence the expected waiting time) for a given change in the elements
can be explicitly computed; this makes possible the use of Monte Carlo
simulations. In some more sophisticated theories, other events which
can result in changes of the elements, such as the capture in some
resonance, are taken into account.
The simplest theories in this class, such as the one by Kessler,
estimate the frequency of the occurrence of close approaches by
modeling the asteroid orbit as if it were a probability cloud. By
averaging over the angular variables 
(mean anomaly), 
and 
, the probability density of the asteroid position is a
function of a,e,I; because of the averaging over , the
probability is independent from longitude. The resulting density
at a radius r from the Sun and at an ecliptic latitude
is given by [Kessler and Cour-Palais], [Kessler 1981]:
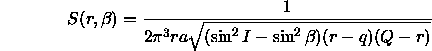
provided r is larger than q=a(1-e) and smaller than
Q=a(1+e), and 
is smaller than I; S is zero if any of
these constraints is not satisfied. Then the most likely number of
close approaches per unit time through a cross section A can be
computed from S and from the relative velocity V of the two
orbits:
The above formula needs to be averaged over the target orbit; in the approximation of a circular orbit for the target planet, with e'=I'=0and with r=a' the semimajor axis of the planet:
where V can be computed from the known value of the velocity of the asteroid orbit when node crossing occurs.
The cross section A for a close approach within an impact parameter
smaller than D is just 
, and the relationship between
impact parameter and minimum distance 
is defined by the
two-body hyperbolic encounter formula:
with GM' the gravitational constant of the planet.
More complicated formulas have been derived to take into account the
eccentricity e' of the orbit of the planet [Steel and Baggaley 1985]; but the
main problem is not in the approximation e'=0. For either r=q or
r=Q or 
the probability density is singular (infinite);
nevertheless the probability of collision is finite, when computed as
an improper integral over the cross section. Thus it is possible to
regularise the apparent singularity of the probability density,
e.g. with the semianalytic method of [Milani et al. 1990].
In practice, the orbits with close approaches near either perihelion
( 
) or aphelion ( 
), and/or with very small I
can have a very large number of close encounters, and the asteroids
whose orbits evolve through one such state have probabilities of
collision comparatively high and difficult to compute exactly (because
of the instability of the computation). If these difficult cases are
handled with care, it is possible to achieve a good accuracy in the
prediction of the deep close approach frequency for a large population
of orbits.
As an example, in [Milani et al. 1990] the average probability of collision
with the Earth for a Near Earth orbit (with 
at least for
some time) is estimated by extrapolating from the sample of close
approaches found in a 200,000 years integration at 
per year per object. The same computation done on the basis
of a modified Kessler theory (with regularisation) gives a probability
of 
per year per object. Other authors give not
very different results []. This means that the
probabilities of collision, when averaged over a long time span and
over a large number of orbits, can be computed in sufficiently
accurate way. The main source of uncertainty on the probability of
collision is in our very incomplete knowledge of the population of
planet crossing objects, and does not depend upon lack of mathematical
knowledge.