Let us consider a planet, e.g. the Earth, on a roughly circular orbit with radius a', and an asteroid with an orbit having the perihelion distance q=a(1-e)<a' and aphelion distance Q=a(1+e)>a'. Under these conditions it is clear that the two orbits could have a common point, but we need to consider the geometry in 3 dimensions.
Each of the two osculating orbits lies in a plane; these two planes being, in general, distinct, have a common line, the line of nodes. The two points of the asteroid orbit on the orbit plane of the Earth are the ascending and the descending node, with distances from the sun:
![]()
with a minimum of q and a maximum of Q, depending upon the value
of the argument of perihelion ![]() . For some values of
. For some values of
![]() a node crossing occurs, when one of the two nodal
distances
a node crossing occurs, when one of the two nodal
distances ![]() and
and ![]() is zero, and one of the two nodes of
the asteroid orbit belongs to the osculating orbit of the Earth.
is zero, and one of the two nodes of
the asteroid orbit belongs to the osculating orbit of the Earth.
In practice, the orbital elements of the asteroid orbit are by no
means constant, they slowly change, mostly as a result of secular
perturbations. Over time scales of ![]() years, in
many cases, the eccentricity e and inclination I undergo small
relative changes, while the argument of perihelion
years, in
many cases, the eccentricity e and inclination I undergo small
relative changes, while the argument of perihelion ![]() performs
several revolutions. In this case the asteroid is a quadruple
crosser, that is there are four times during each period of circulation
of
performs
several revolutions. In this case the asteroid is a quadruple
crosser, that is there are four times during each period of circulation
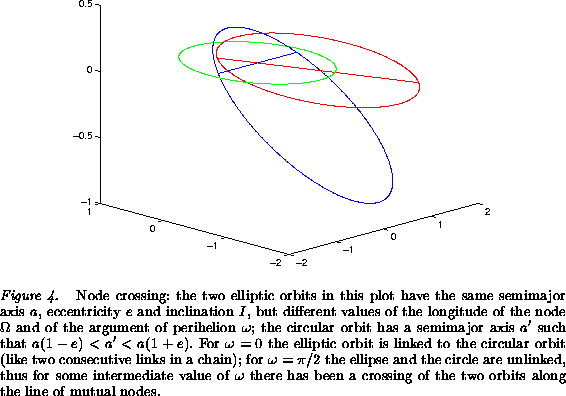
of ![]() when node crossings occur, one for each quadrant (Figure
4). In other cases, the changes in e,I are not negligible, and more
complicated sequences of node crossings can occur, with up to 8 node
crossings per period of
when node crossings occur, one for each quadrant (Figure
4). In other cases, the changes in e,I are not negligible, and more
complicated sequences of node crossings can occur, with up to 8 node
crossings per period of ![]() .
.
The existence of node crossing has three main implications. First, the classical analytical theories to compute short periodic perturbations, secular perturbations, resonances, and solutions of any kind, are either not available or do not work properly. This results from the presence of the singularity of collision, which can occur if the Earth and the asteroid are passing through the common node at the same time. The classical perturbative theories use either series expansion, which are in this case divergent, or averaging, which results in improper (often divergent) integrals.
Second, the possibility of close approaches of the asteroid to the
Earth (also to other planets) results in chaotic motion. The
correlation between the Lyapounov time, over which two nearby orbits
increase their distance on average by a factor ![]() , and the
average time between close approaches, is well understood and has been
tested in a quantitative way by [Whipple 1995] and by [Tancredi 1998].
To explain in a simple way this phenomenon we can resort to a
piecewise 2-body model: during the time span when the nodal distance
is small enough for close approaches, if the phases of the Earth and
of the asteroid along their respective orbits are independent, there
is a finite chance that an encounter occurs. When this happens,
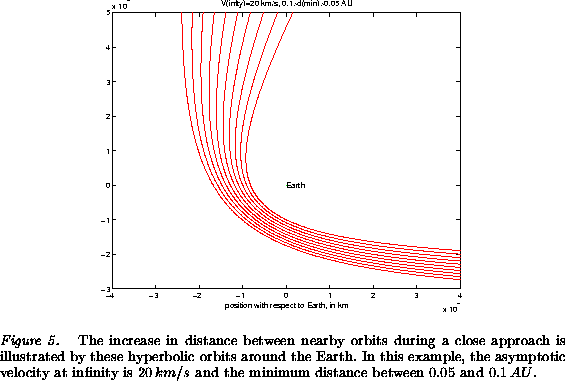
we use a 2-body asteroid-Earth model, in which the asteroid follows
an hyperbolic orbit around the Earth (Figure 5). A bundle of nearby
orbits, with changing impact parameter with respect to the Earth, gets
scattered with distances increased by a factor of 2 to 3, if the
closest approach is inside
, and the
average time between close approaches, is well understood and has been
tested in a quantitative way by [Whipple 1995] and by [Tancredi 1998].
To explain in a simple way this phenomenon we can resort to a
piecewise 2-body model: during the time span when the nodal distance
is small enough for close approaches, if the phases of the Earth and
of the asteroid along their respective orbits are independent, there
is a finite chance that an encounter occurs. When this happens,
we use a 2-body asteroid-Earth model, in which the asteroid follows
an hyperbolic orbit around the Earth (Figure 5). A bundle of nearby
orbits, with changing impact parameter with respect to the Earth, gets
scattered with distances increased by a factor of 2 to 3, if the
closest approach is inside ![]() . This increase of the mutual
distances of nearby orbits is repeated at each occurrence of a close
approach, and each time the factors of increase multiply the previous
increase; this generates an exponential divergence, with Lyapounov
time roughly equal to the average time span between two close
approaches.
. This increase of the mutual
distances of nearby orbits is repeated at each occurrence of a close
approach, and each time the factors of increase multiply the previous
increase; this generates an exponential divergence, with Lyapounov
time roughly equal to the average time span between two close
approaches.
As it is well known from both theory and numerical experiments, chaotic orbits exhibit random behavior, alternating between different states, and also diffusion in the phase space which could result in large relative changes of the orbital elements; all the planet-crossing region of the phase space is indeed a single large chaotic sea, within which every transition if possible, although not necessarily probable. Typically cometary orbits and typical near Earth asteroid orbits can be connected by an evolutionary path including deep close approaches; a good example is the numerically computed orbit of (1862) Apollo shown in [Milani et al. 1989], Figures 5 and 6.
Third, the occurrence of node crossings only for some values of the
argument of perihelion, which has ``secular'' periods of many
thousands of years, results in intermittent behavior. When the nodal
distance is small, frequent close approaches result in a random walk of
all the orbital elements, even the semimajor axis, with occasional
large jumps. When on the contrary the minimum distance between the two
orbits is high (say ![]() ), the asteroid orbit shows all the
features of a regular orbit, which could be represented by a Fourier
series, over which averaging is meaningful, for which proper elements
could be computed. However, this regular behavior only lasts until
the next node crossing, when the orbital elements get random walked to
some other value, from which a new regular orbit segment can begin.
), the asteroid orbit shows all the
features of a regular orbit, which could be represented by a Fourier
series, over which averaging is meaningful, for which proper elements
could be computed. However, this regular behavior only lasts until
the next node crossing, when the orbital elements get random walked to
some other value, from which a new regular orbit segment can begin.
Thus it is very difficult to make use of any statistical representation of the chaotic motion of an Earth-approaching body. If some kind of ergodic principle does hold for this class of orbits, that is if it is possible to exchange averages over regions of the phase space with time averages, this can occur only over times many orders of magnitude longer than the time span between two node crossings; these time spans are in practice too long to be explored numerically, even with the fastest computers of today, unless approximations are introduced which can not represent in a reliable way the real behavior of the exact orbits.
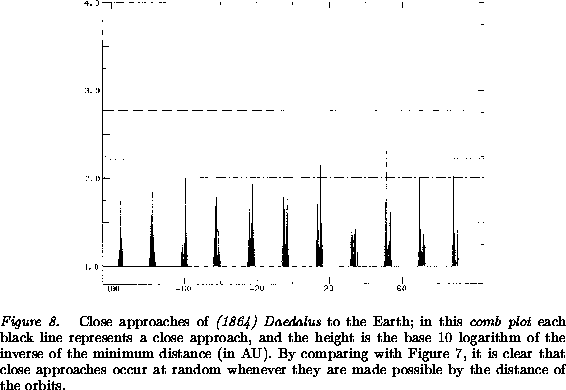
The orbits which show this intermittent behavior, alternating between random occurrence of close approaches near node crossings and regular evolution of the orbital elements (with a almost constant) when nodes are far apart, belong to the Geographos class, according to the classification proposed by [Milani et al. 1989]. This classification is based on the analysis of a set of 89 Earth-crossing orbits numerically computed for 200,000 years; the Geographos class was the most populated one in that sample, which included orbits corresponding -although only approximately- to all the Near-Earth Asteroids known at the time. Thus we can say that the Geographos are the ``normal'' Earth-crossing orbits, although their dynamical behavior is abnormal enough when compared to the one of the main belt asteroids.
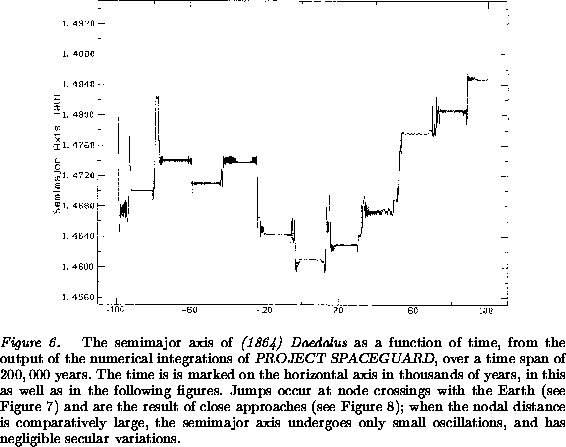
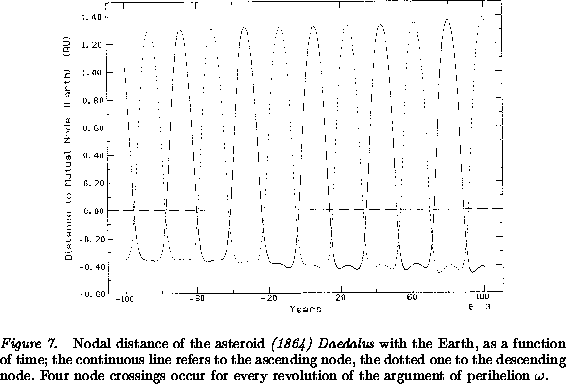
As an example, Figures 6-9 show the
behavior of (1864) Daedalus, a typical Geographos class
asteroid. The semimajor axis (Figure 6) is almost
constant over time spans of several thousand years, then jumps to
significantly different values, in such a way that on the long term it
undergoes a kind of random walk. The nodal distance
(Figure 7) crosses the zero lines near the times of
the jumps in a; the actual occurrence of close approaches follows an
intermittent pattern (Figure 8), which can be
described as random occurrence of encounters whenever the distance
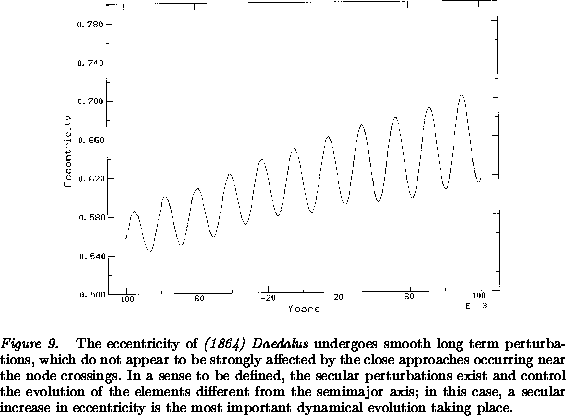
between the two orbits is small enough. The eccentricity
(Figure 9) changes in an almost smooth way, as if
secular perturbations exist in some sense and control the evolution of
the orbital elements ![]() ; the same is true for
; the same is true for ![]() .
.
Two main questions arise from this empirical description of the
dynamical behavior of most Earth-crossing orbits. The first question
is whether it is possible to exploit this alternating, but in some
sense qualitatively uniform, dynamical behavior of the Geographos
class orbits to give some statistical description, as an example to
compute the probability of collision with the Earth. The second
question is whether it is possible to develop an analytical (or at
least semianalytical) theory to account for the ostensibly regular
behavior of the orbital elements ![]() even in
the presence of node crossings and close approaches.
even in
the presence of node crossings and close approaches.