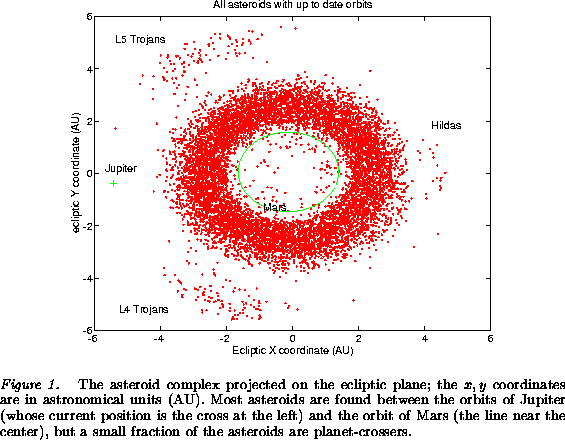

The asteroids are a population of small bodies, whose distribution in space is concentrated in a main belt between the orbits of Mars and Jupiter (Figure 1). A significant number of objects is also found in the two Trojan clouds, roughly at the same distance from the Sun as Jupiter. A comparatively small fraction of this population has orbits which can cross the orbit of some major planet; this is apparent from a plot, such as Figure 2, showing only asteroids down to given size. However the number of asteroids grows in a steep way as the minimum size considered decreases; thus at smaller sizes a comparatively large number of asteroid orbits with perihelia closer to the Sun than Mars, and even the Earth and Venus, have been discovered.
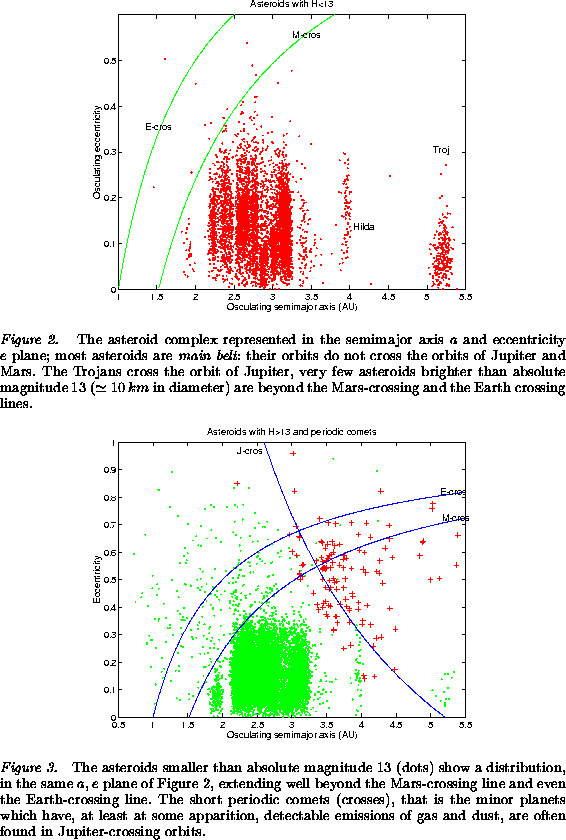
Figure 3 shows the orbital elements (a,e) of
these smaller asteroids, and also of the short periodic comets, which
are bodies of sizes comparable to the asteroids but more easily
visible because of the release of gas and dust; these comets have
often orbits crossing the orbit of Jupiter. A figure such as this one,
showing the orbital elements of many small asteroids, gives a good
intuitive understanding of the transport routes between the main belt
and the Earth neighbourhood: these routes appear as trails in Figure
3; as an example, one route exits the main belt through the 3:1 mean
motion resonance at ![]() , another one exploits the
secular resonance around
, another one exploits the
secular resonance around ![]() .
.
There is a very large literature on the dynamics of main belt asteroids (also of Trojans; see [Milani 1993] and references therein); the dynamical behavior of planet-crossing orbits has been studied only in comparatively recent times, and most of the studies are only descriptions of the output of numerical experiments. Clearly the numerical integration of a large sample of orbits is a necessary but not sufficient condition for understanding the complex problem of planet-crossing dynamics: the familiarity with a large set of examples needs to be supported by a number of theoretical tools. The purpose of this paper is to introduce at least some of the examples of dynamical behavior and some of the conceptual tools to understand them.