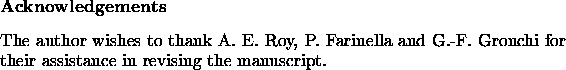The current empirical knowledge, based mostly on numerical integrations, on the dynamical behavior of Earth-crossing orbits -over time scales of a few 10,000 to a few 100,000 years- can be summarized in a classification of the orbit types following [Milani et al. 1989]. For most, but by no means all, of the classes some theory is available, at least as a tool to understand the qualitative features, and as a first approximation. For longer time spans (millions of years) other dynamical phenomena, such as the secular resonances, are relevant, as well as the complex effects of chaotic diffusion.
The classification uses as criteria the main features of the
planet-crossing dynamics: node crossings and close approaches to the
Earth, mean motion resonances with the Earth, the value of q
below/above 
, mean motion resonances and approaches with
Jupiter. The logic is summarized in the block diagram of
Figure 23.
For each asteroid which comes ``Near Earth'' in some sense (say
) the nodal distance is computed as a function of time;
the first question is whether it has node crossings with the Earth.
If there are no node crossings, but the perihelion distance is -at
least for part of the time, during a period of 
- below , the orbit is protected by secular perturbations and is classified
as Kozai class. If the perihelion is above , and the
orbit is not involved in any major mean motion resonance with Jupiter,
then it belongs to the Eros class; as it is the case with the
namesake asteroid (433) Eros, it could become an Earth-crosser
and have a significant probability of impacting the Earth, but only as
a result of secular resonances, acting over time scales of millions of
years [Michel et al. 1996], [Michel et al. 1998].
On the other hand, an asteroid which is not presently Earth-crossing
could be strongly perturbed by a mean motion resonance with Jupiter;
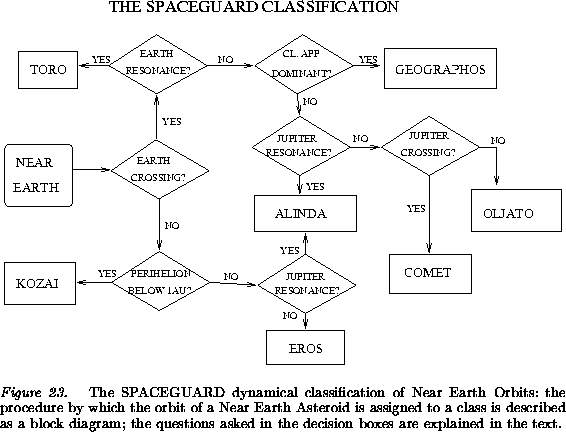
in this case, it belongs to the Alinda class. The behavior of
the semimajor axis of an Alinda is easily identified, because the
resonant perturbations by Jupiter generate large and rapid changes in
a, as in the example in Figure 24. However, the
reason for placing these orbits in a separate class is the very rapid
secular evolution of the eccentricity shown in
Figure 25; as a result, the value of q can decrease
below in a very short time span, typically of the order of a
few 10,000 years.
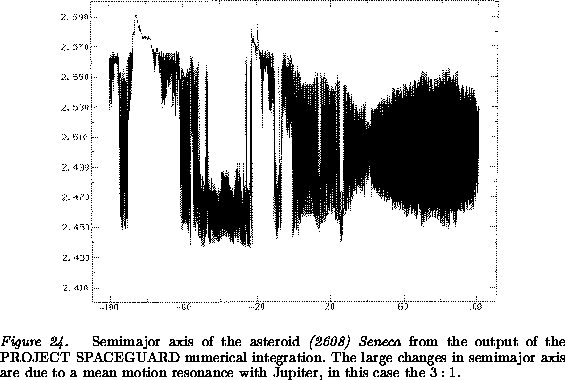
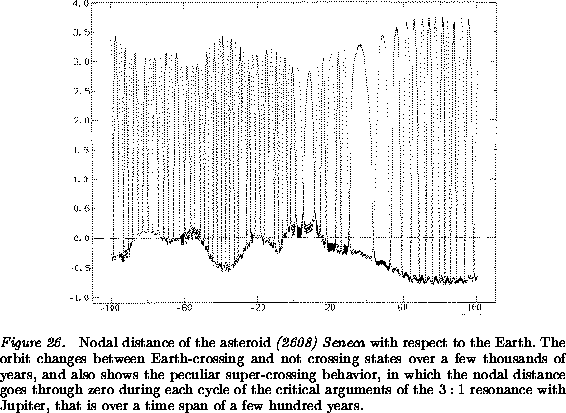
The superposition of the large changes in e and of the
resonant changes in a results in a nodal distance which changes in a
significant way both over time scales of a few hundred years -the
typical period of the resonance critical arguments- and over a time
scale of several thousand years -the period of the secular
perturbations. This can generate the so called super-crossing
behavior, in which node crossings take place at intervals of a few
hundred years, but also a comparatively rapid change between
Apollo orbits (with 
) and Amor orbits (with 
), as shown in Figure 26.
The dynamical behavior of the orbits in mean motion resonance with Jupiter has been studied with semianalytic techniques, e.g. in [Moons and Morbidelli 1995], [Morbidelli and Moons 1993], and is understood at least in qualitative terms. However, the interaction between the resonant, but long distance, perturbations by Jupiter and the short range interactions with the terrestrial planets results in a very complicated behavior of these Kirkwood gap asteroids. The evidence from numerical integrations indicates that there is a synergic effect, by which the orbital elements of the Alinda can change very rapidly, to the point that the distinction between orbits which either are or are not presently Earth-crossing is irrelevant, even over time scales of a few 10,000 years.
Going back to the first decision box in Figure 23, if node crossings with the Earth do occur, the orbit is Toro class if it is sometimes locked in a mean motion resonance, and this resonance is effective to avoid (at least decrease in frequency and depth) the close approaches to our planet. If this is not the case, the time series of a should be examined to decide if the contributions from short range interactions with the terrestrial planets are the dominant source of changes. A formal test based upon correlation analysis could be used, as in [Milani et al. 1990], Section 5; but in most cases visual inspection of the orbital elements plots is enough to decide. The Earth-crossing orbits for which the evolution of a is dominated by close approaches to the Earth (and in some cases to Venus) are Geographos class; the ones where resonant perturbations from Jupiter are dominant are again Alinda class.
The classification scheme described above is logical and for each class there are analytical tools to understand the dynamical behavior. Now come the cases for which the theories are still inadequate, although they can be used to describe the behavior in a qualitative sense. If the evolution of the orbital elements, in particular for the semimajor axis, is neither dominated by the close approaches nor by the mean motion resonances with Jupiter, and nevertheless node crossings take place with the terrestrial planets, the orbit is too strongly perturbed to be described by the currently available theories. If this is due to the occurrence of close approaches to Jupiter, this is a typical cometary orbit (of the so-called Jupiter family); the fact that objects in such orbits can be found in catalogues of asteroids should not be surprising. If it is indeed physically a comet, with a high content of volatiles, this means only that when the perihelion descends below some critical value for sublimation (depending upon the surface composition) the occurrence of an outburst is not necessary, but may depend upon the state of the surface, which in turn may depend upon the dynamical and physical history. On the other hand the same orbit could result from dynamical evolution either from an Alinda class of from a marginally unstable Trojan, and could correspond to an object with asteroidal composition.
There is still one case, corresponding to the last box on the right in Figure 23: there are orbits which are not resonant with Jupiter (at least not for a significant span of time), do not undergo orbital changes dominated by close approaches to the terrestrial planets, and are neither Jupiter crossing nor Jupiter approaching; according to the classification of the PROJECT SPACEGUARD they form the Oljato class, from the namesake asteroid (2201) Oljato; see [Milani et al. 1989], Figure 14. These orbits have an eccentricity very large and changing secularly, low to moderate inclination, and very frequent close approaches to the terrestrial planets; they can be described as comet-like orbits with aphelia just decoupled from Jupiter, and therefore are likely to be a very important step in the dynamical pathway of transition between Jupiter family comets and Near Earth asteroids.
The problem is, these are the orbits we are not yet able to model
analytically in all their complexity, because the combined effects of
secular resonances and close approaches to the terrestrial planets play
an essential rôle in the evolution of the Oljato class
orbits. Theories are available for secular resonances, especially the
most important one, resulting from the argument of perihelion
of the asteroid revolving around the Sun with
the same average rate as the one of Saturn [Morbidelli 1993], but
these theories are not consistently applicable when close approaches
with the Earth can take place; numerical experiment confirm the
existence of the secular resonances even where node crossing can occur
[Froeschlé et al. 1995]. In the near-Earth and near-Mars region other
secular resonances, locking the asteroid perihelium and node to the
ones of the terrestrial planets, are known to occur [Michel and Froeschlé 1997],
[Michel et al. 1998], but the theory exists so far only for low
eccentricities and non-crossing orbits. The Oljato class orbits are
often found in the Taurid region [Valsecchi et al. 1995]; large scale
changes in the orbital elements, resulting from resonances, provide
the entrance path into this region, with orbits coming both from the
asteroid main belt and from the Jupiter family of comets, and the exit
path: collision with the Sun [Farinella et al. 1994], hyperbolic expulsion
after a close approach to Jupiter, and less frequently collision with
one of the terrestrial planets.
I would like to conclude by saying that the dynamical classification of [Milani et al. 1989] is an useful tool to understand the dynamics of the Earth-approaching objects, but it needs to be stressed that all these are strongly chaotic orbits, and that all the orbital elements can undergo large relative changes, as a result of either deep close approaches or the action of some resonance. Thus transitions can occur (see [Milani et al. 1989], Figure 16), and indeed often occur, between the dynamical classes. The Toro and Alinda classes are especially unstable, with typical residence times in the class <100,000 years. As an example, transitions can occur between the Alinda, comet-like and Oljato classes; that is, an asteroid coming from some Kirkwood gap can be injected into a comet-like orbit as well as ending up as a meteorite.
