2.3 Close approach manifold

The closest approach point on the nominal orbit with initial conditions X^* (solution of the least squares fit) belongs by definition to the MTP. The closest approach points with nearby initial conditions X, however, do not in general lie on the MTP, although they are nearby (for small $\Delta X$). Thus the intercept with the MTP in general is not at the minimum distance; the fact that some confidence boundary does not intersect the disk with radius r=R_P(where R_P is the radius of the approached planet) does not guarantee that there is no impact in a point outside the MTP.

Although the set of possible close approach points is not a linear subspace of the phase space, it can be represented on the MTP. We have chosen a representation such that the closest approach distance is the planetocentric distance of the representative point on the MTP: if $(r_{MTP}, \psi_{MTP})$ are planetocentric polar coordinates on the MTP, and r_CL is the closest approach distance on the same orbit, we use the point with polar coordinates $(r_{CL}, \psi_{MTP})$. In practice, the MTP intercept and the close approach manifold representative point are very close, with the exception of very deep and/or very slow encounters.

  

Figure: Modified target plane analysis for the possible close approach of the lost asteroid 1978 CA with the Earth on September 3, 1997. The linear confidence ellipse for $\sigma =3$ is shown with a dotted line: note that it extends well beyond the d=0.1 AU circle. The semilinear boundary on the MTP and that on the close approach manifold (also for $\sigma =3$) are drawn in full line; they cannot extend beyond d=0.1 AU because they are computed only for orbits entering the close approach sphere. Note that the close approach manifold boundary is, by definition, closer to the Earth than the MTP boundary.

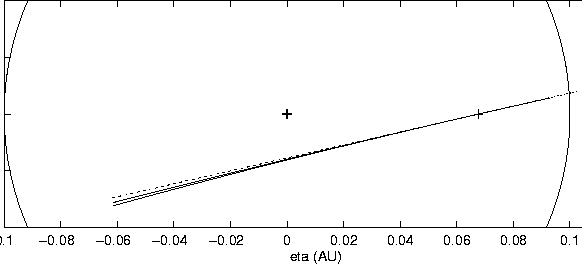Figure 1 shows the target plane analysis outlined in this Section for the lost asteroid 1978 CA, which can have had a close approach to the Earth on September 3, 1997. In the plot we have drawn the intercept on the MTP of the nominal orbit (cross), the linear confidence ellipse (dotted line), the semilinear confidence boundary on the MTP, and the representation of the close approach points of the same orbits, all for $\sigma =3$. For small enough displacements from the nominal orbit the linear approximation is good enough; for larger displacements the differences between linear and semilinear approximation, and between the MTP and the close approach manifold, are visible. The maximum deviation of the semilinear boundary on the MTP from the linear ellipse is as large as the Earth-Moon distance.

In this case the semilinear approximations show only moderate deviations from the linear approximation, essentially because 1978 CA could not have a very close approach (the MOID is 0.15AU). Nevertheless, this lost asteroid could have passed the Earth at a quarter of the distance predicted using the nominal orbit. Any attempt to predict in which direction in the sky astronomers should have looked to observe this asteroid when it was apparently brightest would have failed, because there are solutions compatible with the 1978 observations arriving from opposite directions. Indeed this asteroid has not been recovered, although it could have been quite bright.