


Next: 2.2 The checking algorithm
Up: 2. The filtering procedure
Previous: 2. The filtering procedure
2.1 First selection
The first step of the filtering procedure consists of a rough
comparison of the available short arc observations with the
predictions resulting from the available nominal orbit. This means we
need two catalogs to start with. One catalog contains the nominal
orbits, obtained by a least squares fit to the observations of arc
1. The second catalog contains the attributables, which are
single observations computed in such a way that they can represent
all of the observations of arc 2. Before giving a more precise
description of the content of an attributable, we need to understand
how it is going to be used, both in the first and in the second
filtering stages.
In the first step, the nominal orbits have to be propagated to the
epoch of the attributables. The problem is that the number of
attributables is the number of short arc discoveries. We use all the
arcs containing at least two observations2
not degraded in accuracy and with a time span not exceeding
8-10 days. Thus, the total number of attributables is usually more than
70,000 (e.g., in the April 2000 update, it was 74,656); moreover,
they are unevenly distributed in time, much denser
in recent times. Propagating each orbit to each one of these times
would be very inefficient. Typically we perform about 5,000
integration steps for each orbit, and we would be forced either to
perform integration steps shorter than the ones optimal for
computational efficiency, or to use interpolation procedures which are
also computationally expensive. Therefore in the attributable record we
include an extrapolated observation for the nearest time which is an
integer multiple of a fixed 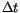 (we currently use 10
days).
To obtain this, we first compute the straight lines in the
(we currently use 10
days).
To obtain this, we first compute the straight lines in the
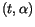 and in the
and in the
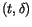 planes best fitting to the data
of arc 2. Then we define a central time tm as the arithmetic
mean of the observation times, neglecting the observations which are
degraded in accuracy (with weights corresponding to RMS errors larger
than 4 arc seconds). We then identify the time tstep multiple of
planes best fitting to the data
of arc 2. Then we define a central time tm as the arithmetic
mean of the observation times, neglecting the observations which are
degraded in accuracy (with weights corresponding to RMS errors larger
than 4 arc seconds). We then identify the time tstep multiple of
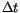 and closest to tm, and compute the value on the best
fitting lines of
and closest to tm, and compute the value on the best
fitting lines of
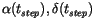 .
The use of a linear fit over a time span of up to
.
The use of a linear fit over a time span of up to
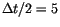 days
is inaccurate, but the first filtering stage uses a control d<R on
the distance d between prediction and observation which is large,
e.g., R=1.5 degrees (d is computed by the usual metric on the
celestial sphere:
days
is inaccurate, but the first filtering stage uses a control d<R on
the distance d between prediction and observation which is large,
e.g., R=1.5 degrees (d is computed by the usual metric on the
celestial sphere:
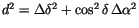 ).
Of course, the use of such a loose control results in many false
positive, but the area of the region within 1.5 degrees from a given
position on the celestial sphere is only
).
Of course, the use of such a loose control results in many false
positive, but the area of the region within 1.5 degrees from a given
position on the celestial sphere is only
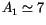 square degrees.
Taking into account that most asteroid detections take place in a band
around the ecliptic which has an area of the order of 10,000
square degrees, this explains the ratio between pairs examined and those
passing the first filter. Thus the value of 1.5 degrees is
appropriate to make the second stage of our procedure efficient.
We have expended a significant effort to make the orbit computation
efficient by optimizing the orbit propagation routines of the
OrbFit software. Nevertheless, the first filter is a CPU intensive
step of the attributions procedure since the orbit computation must be
accurate and the attributables are spread over a total time span of
about 100 years. As an example, during the May 2000 update we have
used for this stage about 50 CPU hours (spread on three different
computers). However, it is not necessary to search for attributions to
all the orbits for all the attributables every month, as we did in
April and May 2000; only the orbits changed since last month need to
be tested on all attributables, and the new attributables need to be
tested for all the orbits.
square degrees.
Taking into account that most asteroid detections take place in a band
around the ecliptic which has an area of the order of 10,000
square degrees, this explains the ratio between pairs examined and those
passing the first filter. Thus the value of 1.5 degrees is
appropriate to make the second stage of our procedure efficient.
We have expended a significant effort to make the orbit computation
efficient by optimizing the orbit propagation routines of the
OrbFit software. Nevertheless, the first filter is a CPU intensive
step of the attributions procedure since the orbit computation must be
accurate and the attributables are spread over a total time span of
about 100 years. As an example, during the May 2000 update we have
used for this stage about 50 CPU hours (spread on three different
computers). However, it is not necessary to search for attributions to
all the orbits for all the attributables every month, as we did in
April and May 2000; only the orbits changed since last month need to
be tested on all attributables, and the new attributables need to be
tested for all the orbits.



Next: 2.2 The checking algorithm
Up: 2. The filtering procedure
Previous: 2. The filtering procedure
Andrea Milani
2001-12-31