Let us suppose the nominal orbit with initial conditions X* has a close approach with some planet, which is defined as a passage within a given distance d. Practical limits for the selection of the distance d are that it must not be too large to result in the possibility of simultaneous close approach with two planets, but large enough to allow the detection of close approaches for the nearby orbits; values between 0.03 and 0.1 AU are suitable for the terrestrial planets. The distance from the planet r(t,X*) has at least one minimum lower than d, at some time t=t*. A practical algorithm to compute t* is the regula falsi applied to search for the zeros of the function dr/dt; it is easy to discriminate the minima from the maxima of r by checking the sign of dr/dt. If there are multiple minima, a particular one has to be selected or ddecreased until only one minimum remains.
We define as Modified Target Plane (MTP) the plane through the center
of the approached planet and perpendicular to the velocity vector of
the encountering body at the closest approach time t*. This
definition is the same used by [Yeomans and Chodas 1994] (they call it target
plane), and is a modification of the target plane used in Öpik's
theory of close encounters [Öpik 1976]; the latter is the plane
through the planet and perpendicular to the unperturbed velocity
vector. These two planes are of course close to each other for shallow
encounters.
Once an MTP has been selected, we can use cartesian orthogonal
planetocentric coordinates
![]() such that at closest
approach on the nominal orbit
such that at closest
approach on the nominal orbit
The choice of the orthogonal coordinates
![]() in the MTP is
arbitrary; for the figures of this paper, we have selected the axes in
such a way that
in the MTP is
arbitrary; for the figures of this paper, we have selected the axes in
such a way that
![]() ,
that is,
,
that is,
![]() is along the vector from the planet to the nominal closest
approach position. If the MTP is crossed only once during the close
approach, we can select an orientation such that
is along the vector from the planet to the nominal closest
approach position. If the MTP is crossed only once during the close
approach, we can select an orientation such that ![]() .
Low
velocity encounters, which can result in multiple minima of the
planetocentric distance and/or multiple crossings of any selected MTP,
would introduce complications in the geometry of the confidence
boundaries which are beyond the scope of this paper, focused on
encounters of NEO with the terrestrial planets; in the cases we are
interested in,
.
Low
velocity encounters, which can result in multiple minima of the
planetocentric distance and/or multiple crossings of any selected MTP,
would introduce complications in the geometry of the confidence
boundaries which are beyond the scope of this paper, focused on
encounters of NEO with the terrestrial planets; in the cases we are
interested in, ![]() is larger than the planetocentric parabolic
velocity.
For orbits close to, but different from, the nominal one, the time
at which the MTP is crossed can be different from t*, and is a function
of the initial conditions: t=t(X), implicitly defined by the equation
is larger than the planetocentric parabolic
velocity.
For orbits close to, but different from, the nominal one, the time
at which the MTP is crossed can be different from t*, and is a function
of the initial conditions: t=t(X), implicitly defined by the equation
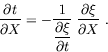
The map onto the MTP is expressed by the functions
![]() ,
that can be shown to be differentiable as follows, provided
the MTP crossing is transversal:
,
that can be shown to be differentiable as follows, provided
the MTP crossing is transversal:
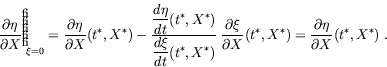
In practice this means that, given the state transition matrix,
solution of the variational equation along the nominal orbit at time
t=t*, the partial derivatives of the map on the MTP are easily
computed. As for the computation of the map itself for an orbit with
initial conditions ![]() ,
the solution t(X) of the equation
,
the solution t(X) of the equation
![]() is obtained by iterating a regula falsi as above.
is obtained by iterating a regula falsi as above.
We shall therefore assume from now on that the position of the
intercept on the MTP is a 2-dimensional vector
![]() ,
and
that Y is a function of the initial conditions X, known together
with its partial derivatives:
,
and
that Y is a function of the initial conditions X, known together
with its partial derivatives: