4.1 MTP analysis with the early data

The least squares fit using only the 27 observations up to July 6 has an RMS of the residuals of 0.69 arc seconds; we use the weighting corresponding to 1 arc second for consistency with our approach of Section 3.1, although in a simulated case the residuals have been manufactured by some random number generator and they are likely to be more Gaussian than in any real example. The conditioning number of the covariance matrix is $3\times 10^9$, with a largest eigenvalue $\sigma_1^2=1.2\times 10^{-5}$, thus the confidence ellipsoid is quite large and we are really testing the boundaries of applicability of our semilinear method.

Propagation of the nominal orbit in the near future reveals close approaches repeating more or less every 4 years; the first one is 1996, at a minimum distance 0.030 AU; the closest one is on October 3, 2004, at a distance 0.021 AU. The close approach analysis of the 1996 encounter indicates that there is nothing to worry about for that year. The $\sigma =3$ linear confidence ellipse on the MTP, centered on the 0.030 AU nominal closest approach, has semiaxes of 184 km and 0.13 AU, that is the long semiaxis is much longer than the nominal miss distance. The long axis, however, is in a direction forming an angle of $15^\circ$ with the direction towards the Earth. As a result, both the linear and the semilinear confidence boundaries on the MTP come no closer than $\simeq 0.008$ AU from the Earth.

  

Figure: The $\sigma =3$ confidence boundaries on the MTP for the 2004 encounter of the fictitious asteroid 1992 KP₄, obtained by using observations only until July 6, 1992. The long axis of the linear ellipse (dotted line) is tangent to the axis of the semilinear boundary (dotted line with cross marks) at the nominal close approach point (marked with a circle). Note that the range of values on the $\eta$ axis is much larger than that of the $\zeta$axis. For this reason the circle -around the origin and representing the Earth surface- is distorted so as to look like a segment.

The close approach analysis of the 2004 encounter gives a much less comfortable result. The $\sigma =3$ linear confidence ellipse on the MTP, centered on the d_n=0.021 AU nominal closest approach, has semiaxes of 590 km and 0.19 AU, that is the long axis is again much longer than the nominal miss distance. The size of the ellipse would not matter if, as in the previous case, the long axis were oriented in a safe direction. The worrisome feature is, for the 2004 encounter the ellipse points almost exactly towards the Earth: the angle between the long axis and the direction to the center of the Earth is only $\beta=0.\!^\circ 2$. Nevertheless, the linear confidence boundary does not touch the Earth surface, missing it by less than one Earth radius; to check this, it is enough to compute $d_{n}\,\sin \beta=0.021\, AU\times \sin 0.\!^\circ 2= 7.8\times 10^{-5}\, AU=1.8\; R_\oplus$.

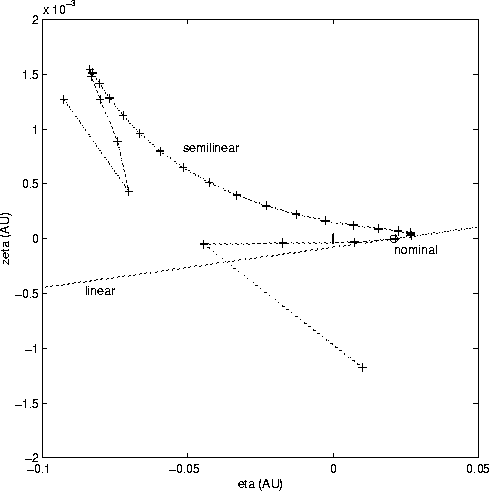
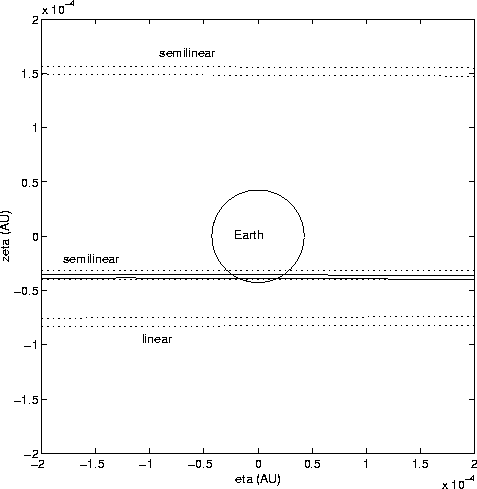
The nonlinearity of the map onto the MTP is impressive, as shown in Figure 9: the linear and the semilinear boundary are close only in the immediate neighbourhood of the nominal solution, everywhere else they develop in a qualitatively different way; the range of closest approach distances is completely different (note the different scales on the two axes). Looking at an enlarged view (Figure 10) we see that the semilinear boundary intersects the Earth surface, while the linear ellipse does not, as predicted by the simple calculation performed above. In this particular case, the linear confidence analysis with the observations up to July 6 would lead to exclude the possibility of a collision which, in the simulation, actually takes place. The semilinear analysis would correctly conclude that an impact cannot be excluded.

  

Figure: An enlargement of the MTP boundaries of Figure 9. The linear ellipse based upon the observations until July 6 misses the Earth by a small margin (dotted lines in the lower part of the Figure); the semilinear boundary with the same data (dotted lines) is so much bent, that it intersects the window of this plot twice. The semilinear boundary based upon all the 1992-93 observations (continuous lines) is inside the lower intersection of the semilinear boundary obtained with fewer observations.