The question still pending, after some reasonable confidence boundary
(for either ![]() or
or ![]() ,
as discussed above) on the MTP
has been computed, is whether an impact is possible, given the
available observations. If the 1990 precovery observations are taken
into account, this possibility can be excluded without complicated
arguments. For the solution using the 1997-98 data only, we have
computed the confidence boundaries, in both the linear and the
semilinear approximations, corresponding to
,
as discussed above) on the MTP
has been computed, is whether an impact is possible, given the
available observations. If the 1990 precovery observations are taken
into account, this possibility can be excluded without complicated
arguments. For the solution using the 1997-98 data only, we have
computed the confidence boundaries, in both the linear and the
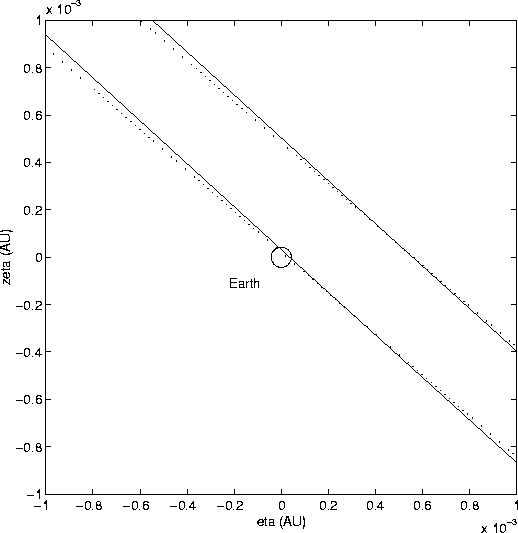
semilinear approximations, corresponding to ![]() ;
as shown in
Figure 8, only for values of the
;
as shown in
Figure 8, only for values of the ![]() parameter
this high does an impact become possible, in both approximations.
parameter
this high does an impact become possible, in both approximations.
 |
From the discussion of the previous subsections it should be clear that we are not fully convinced that it is possible to give a quantitatively rigorous estimate of the probability of an impact for the 2028 encounter of 1997 XF11 with the Earth. Even excluding the 1990 precovery observations, the probability is a very small number; to compute it, one needs to use the very extreme tails of an assumed Gaussian distribution. The fact is, the observation errors do not follow a Gaussian distribution, so much so that whenever a residual is above 3 times the RMS of 0.5 arc seconds we discard it. If a single residual were of the order of 60 times the assumed weight of 1 arc second, no one on Earth would include it in an orbital solution, but rather think that the observation belongs to another asteroid.
If, on the other hand, all the observations conspired to allow an
impact in 2028, then the RMS value of the residuals would become no
less than ![]() arc seconds; this is so far along the tail of a
Gaussian distribution with RMS 0.5 that the formal probability would
be a very small number, but this would stretch the application of
Gaussian statistics far beyond the region where it correctly
represents the observation errors. Rather than using an extremely
small number to describe the probability of such a solution, we would
rather describe the situation in the following way. Accepting an
impact solution as compatible with the 1997-98 observations would be
equivalent to believing that there has not been any progress in
astrometry since the second half of the eighteenth century, when
typical observation errors were
arc seconds; this is so far along the tail of a
Gaussian distribution with RMS 0.5 that the formal probability would
be a very small number, but this would stretch the application of
Gaussian statistics far beyond the region where it correctly
represents the observation errors. Rather than using an extremely
small number to describe the probability of such a solution, we would
rather describe the situation in the following way. Accepting an
impact solution as compatible with the 1997-98 observations would be
equivalent to believing that there has not been any progress in
astrometry since the second half of the eighteenth century, when
typical observation errors were ![]() arc seconds.
arc seconds.
We find this argument, based on the size of the residuals required to allow an Earth impact, more convincing than a statement of a tiny impact probability computed from an inappropriate application of Gaussian statistics.